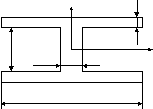
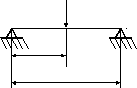
3.1.4. Двутавровая балка
Стальная призматическая балка с горизонтальной осью симметрии проектируется на сосредоточенную нагрузку, как показано на рис. 3.4.
k2t
P y
H x
L/2 t
L
k1h
Рис. 3.4. Схема нагружения балки и ее параметры
Балка должна иметь минимальный вес при ограничениях на изгибающие ограничения в полках и на местную потерю устойчивости полок и стенки. Из четырёх переменных, определяющих форму поперечного сечения, в качестве переменных проектирования выбираются переменные hиt, аk1иk2считаются заданными.
Ограничение на напряжение задаётся неравенством
,
где Ми– изгибающий момент.
Выражение для критического напряжения
при выпучивании имеет вид
,
где Kp– коэффициент выпучивания: для полокКр= 0,385, для стенкиКр= 3,62.
Ограничения на местную потерю устойчивости находятся из выражений:
для полок
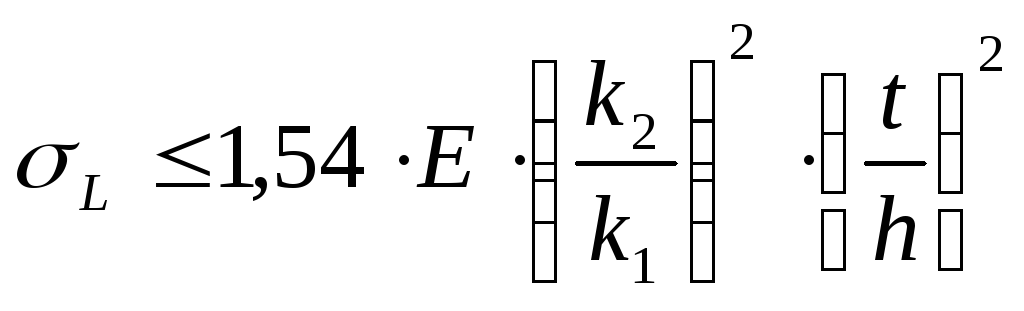,для стенки
.
Используя
обозначения:
,
,
,
,
определить оптимальное решение.
Для решения этой задачи используем метод Куна-Таккера. ЦФ имеет вид
f(h,t) = ρlS = ρl(2k1k2th)+ ρlht = ρlβht = Aht,
где A=ρlβ.
В данном случае ограничения находятся из выражений:
g1(h,t)=α/(ht²)-KpE(t/b)²;
g2(h,t)=α/(ht²)-1.54(k2/k1) ²(t/h)²=α/(ht²)-η(t/h)²;
g3(h,t)=α/(ht²)-21.7E(t/h)²=α/(ht²)-ν(t/h)².
Функция Лагранжа записывается в виде
L=Aht-ν1(α/(htІ)- KpE(t/b)І)-ν2(α/(htІ)-η(t/h)І)-ν3(α/(htІ)-ν(t/h)І).
L/h=At+ ν1α/tІhІ+ ν2(α/(hІtІ)-ηtІ/hі)+ν3(α/(hІtІ)-νtІ/hі);
L/t= Ah+ν1α/tіh+ ν2(α/(htі)-ηt/hІ)+ν3(α/(htі)-νt/hІ).
Проанализируем все возможные сочетания, которые могут иметь место при равенстве нулю одного из сомножителей.
1. ν1>0,ν2>0, ν3>0; g1=0, g2=0, g3=0.
2. ν1=0,ν2>0, ν3>0; g2=0, g3=0.
3. ν1>0,ν2=0, ν3>0; g1=0, g3=0.
4. ν1>0,ν2>0, ν3=0; g1=0, g2=0.
5. ν1=0,ν2=0, ν3>0; g3=0.
6. ν1=0,ν2>0, ν3=0; g2=0.
7. ν1>0,ν2=0, ν3=0; g1=0.
8. ν1=0,ν2=0, ν3=0.
При заданных параметрах нагружения и характеристик материала анализ представленных вариантов позволяет получить оптимальное решение; при этом расчет проводится аналогично задаче п. 3.1.3.
3.1.5. Колодочный тормоз
В данном расчете ЦФ является взвешенная сумма массы обода колодочного тормоза, изображенного на рис. 3.5, и термоупругого напряжения, определяемая по формуле:
f(x)=a1BDh+a2 ,
-
Рис. 3.5. Колодочный тормоз
где a1 и а2 - весовые коэффициенты; ρ - плотность материала обода шкива; σφφ - термоупругое напряжение обода шкива.
Величина σφφ находится из выражения
,где α - температурный коэффициент линейного расширения материала обода;Е - модуль Юнга; μ- коэффициент Пуассона;t1,t2-температура обода шкива соответственно до и после торможения.
Температура обода определяется из условия равенства аккумулируемой теплоты в единицу времени и мощности, затрачиваемой на преодоление сопротивления трения:
,
где с - удельная теплоемкость материала обода; k - коэффициент, учитывающий долю аккумулируемой ободом энергии; ω0 - начальная угловая скорость обода; τ - продолжительность торможения; mт - момент трения в конце торможения, определяемый по формуле:
где Р - давление колодок на поверхность тормозного обода; f - коэффициент трения между поверхностями колодки и тормозного обода.
Из
условия прочности на изгиб 
можно
получить 
.
На оптимизируемые параметры накладывается ограничение - крутящий момент не превышает момента трения:
.
Методом геометрического программирования определить параметры оптимальной конструкции тормоза: h, D и В, используя при этом указание, согласно которому модель оптимизации необходимо представить в виде:
В этих выражениях постоянные С определяются по следующим формулам:
;
;
.
Поскольку в данной задаче степень трудности d=0, то двойственные переменные находятся из системы линейных уравнений, включающей условия нормализации и ортогональности:
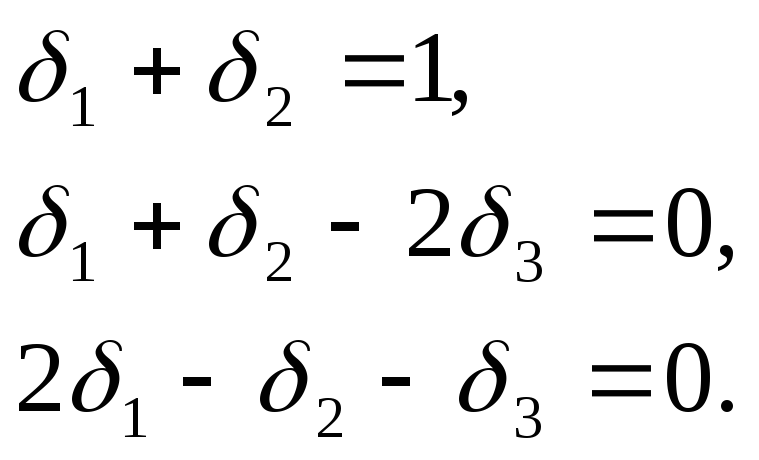
Решением данной системы являются следующие значения:
Максимум двойственной функции находится по формуле
.
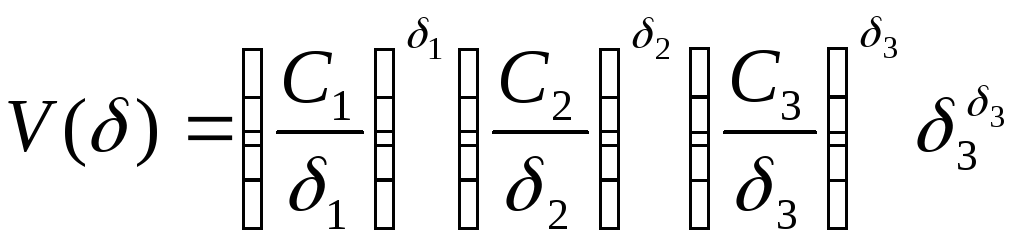На основе выполненного анализа можно записать
.
Для определения оптимальных параметров тормоза используются следующие соотношения:
;
.
Решая эту систему относительно D и h, можно получить
;
.
Следовательно, расчетные формулы имеют вид
;
;
.
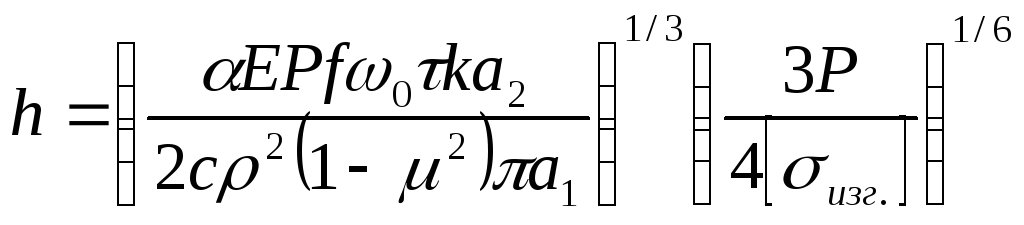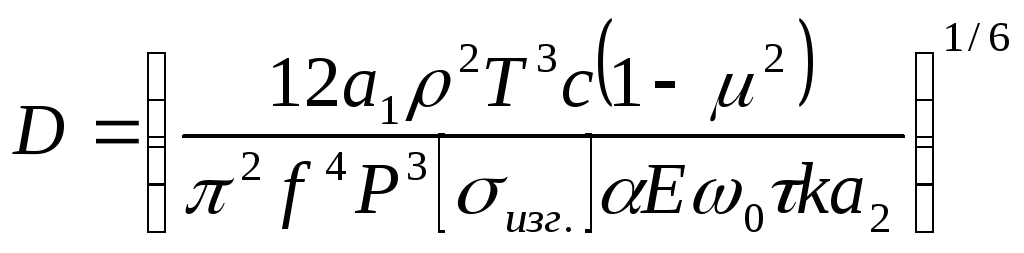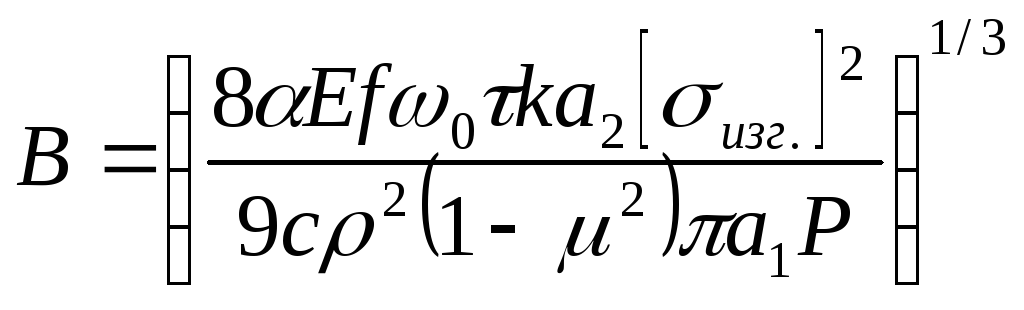В зависимости от исходных данных представленные аналитические формулы позволяют рассчитать оптимальную конструкцию тормоза.