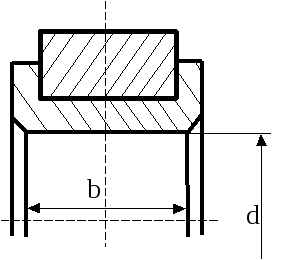
3.1.6. Подшипник скольжения

Рис. 3.6. Подшипник скольжения

При проектировании высоконагру-женных подшипников скольжения (рис. 3.6) в качестве ЦФ принимается взвешенная сумма интенсивности изнашивания цапфы и прогиба вала: , где а1, и а2 - весовые коэффициенты; Δ -интенсивность изнашивания цапфы; y0 - прогиб вала в подшипнике.

Величина Δ находится из выражения

где v - износ цапфы на единицу мощности, затрачиваемой на трение; f - коэффициент трения; F - радиальная сила, действующая на подшипник; - радиус подшипника; ω- угловая скорость вала.

Коэффициент трения определяется по формуле

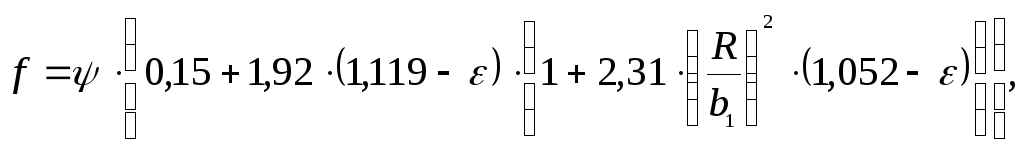
где ψ - относительный зазор; ε – относительный эксцентриситет; .

Прогиб вала в подшипнике находится из выражения

где Е – модуль продольной упругости материала вала.

На оптимизируемые параметры накладывается ограничение

где - среднее давление на подшипник; - допустимое давление.

Задача состоит в том, чтобы методом геометрического программирования определить параметры оптимального подшипника скольжения, приняв следующую модель оптимизации:

Степень трудности этой задачи d = 4-(2+1) = 1.

Двойственная функция V() = (C₁/₁)^1 (C₂/₂)^2 (C₃/₃)^3 C₄^4.

При двойственных ограничениях 0  ₁, 0  ₂ 0  ₃ , 0  ₄ система уравнений, состоящая из условий нормализации и ортогональности, имеет вид

₁+₂+₃ = 1;

₁+3₂-4₃ - ₄ = 0;

-2₂+3₃ -₄ = 0.

Приняв ₃ = r, получим: ₁ = 5/4 – r; ₂ = -1/4 + 2r; ₄ = 0,5 – r.

Уравнение равновесия для данной задачи после подстановки выражений для _iимеет вид

4(5-12r)^-3 (8r-1)² r = C₂² C₃/ (C₁³ C₄),

где ;;

; .

После определения правой части уравнения по заданным исходным данным решается нелинейное уравнение относительно r , а затем вычисляются значения двойственных переменных, что позволяет найти величины оптимизируемых параметров и ЦФ.

3.1.7. Червячно-цилиндрический редуктор

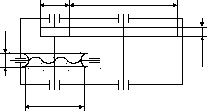
В задаче определения оптимальных значений параметров червячно-цилиндрического редуктора (рис. 3.7) в качестве ЦФ принята суммарная стоимость материалов обеих ступеней:

где К₁´- весовой коэффициент, учитывающий стоимость единицы массы червячного колеса и червяка; К₂´- весовой коэффициент, учитывающий стоимость единицы массы колес цилиндрической ступени редуктора; т₁₂ - масса червячного колеса; т₂₁ и т₂₂ – масса соответственно ведущего и ведомого колеса цилиндрической ступени.

В червячной ступени стоимость червяка учитывают при определении весового коэффициента червячного колеса, обод которого в большинстве случаев изготовляют из дефицитных материалов с антифрикционными свойствами.

При введении коэффициента f = К₁´/ К₂´ параметр К определяется по формуле

d21d22 b1 b2 d12 Рис. 3.7. Схема червячно-цилиндрического редуктора

Масса каждого колеса находится из выражения

где - индекс ступени;  - индекс колеса; ρ – плотность материала колеса; В – ширена колеса; d – диаметр делительной окружности колеса.

Конструктивные параметры определяются по формулам

B₁=_dd₁₁ , d₁₂=z₁₂m_s1 , z₁₂=u₁z₁₁, d₁₁=qm_s1 ,

где В₁ – ширина червячного колеса; _d – коэффициент ширины; d₁₁ – диаметр червяка; d₁₂ – диаметр делительной окружности червячного колеса; u₁ – передаточное число червячной ступени; z₁₁ – число заходов червяка; z₁₂ – число зубьев червячного колеса; q – относительная толщина червяка; m_s1 – осевой модуль зацепления.

Обозначив: а также учитывая: В₂ = _aa₂ и d₂₂ = u₂d₂₁ ,

первое слагаемое ЦФ имеет вид

,

а сумма второго и третьего слагаемых

где ρ₁ – плотность материала колес цилиндрической ступени; _а – коэффициент ширины зуба; d₂₁ и d₂₂ - диаметр делительной окружности соответственно ведущего и ведомого колеса цилиндрической ступени; а₂ – межосевое расстояние цилиндрической ступени; и₂ – передаточное число цилиндрической ступени.

Из расчёта цилиндрической зубчатой передачи на контактную прочность можно записать

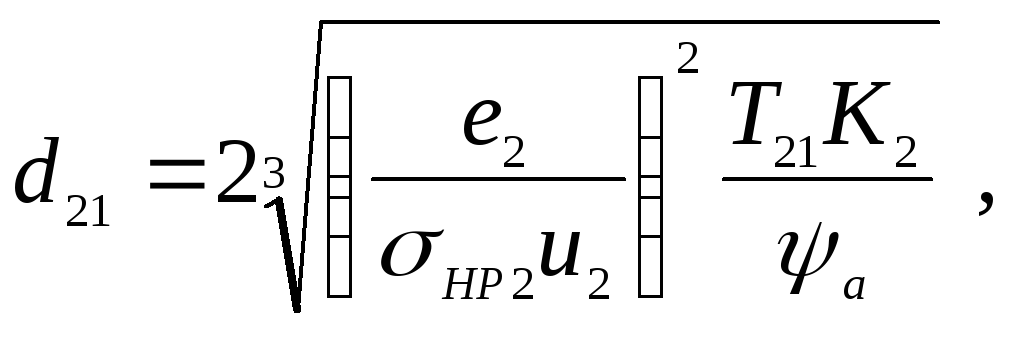
где е₂ = 340·10³; _НР2 – допустимое контактное напряжение материала зубьев шестерни цилиндрической ступени; Т₂₁ – крутящий момент на ведущем валу цилиндрической ступени редуктора; К₂ – коэффициент нагрузки.

Момент на ведущем валу определяется по формуле

Т₂₁ = и₁₁Т₁₁,

где Т₁₁ – крутящий момент на ведущем валу редуктора; ₁ – КПД первой ступени передачи.

Следовательно, сумма масс колеса и шестерни передачи находится из выражения

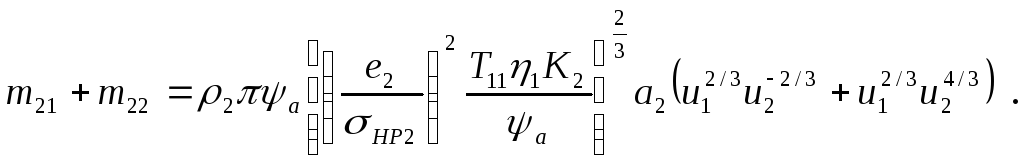
Итак, ЦФ имеет вид

где

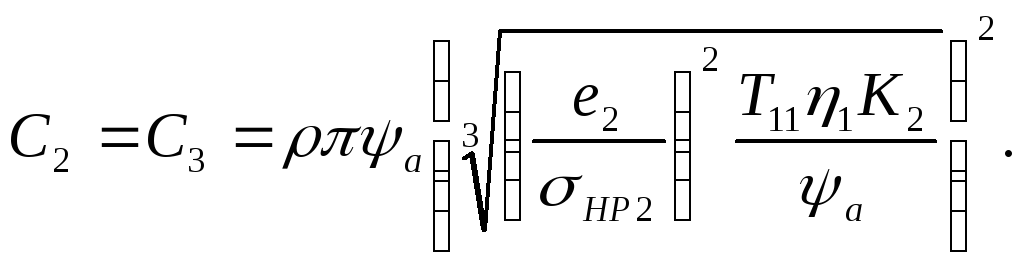
В качестве ограничений на параметры оптимизации и₁, и₂, t и а₂ примем ограничения на контактные напряжения, возникающие в зацеплениях червячной и цилиндрической передач, и на общее передаточное число и:

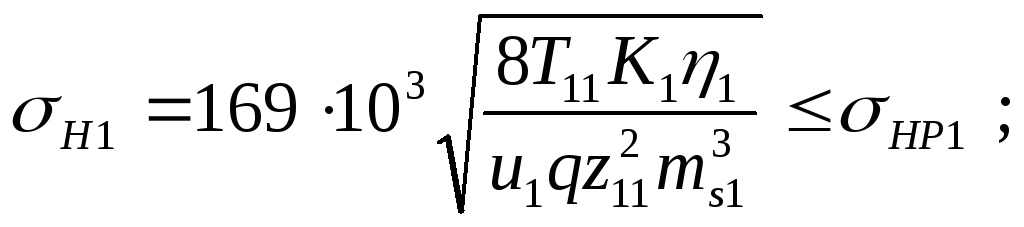
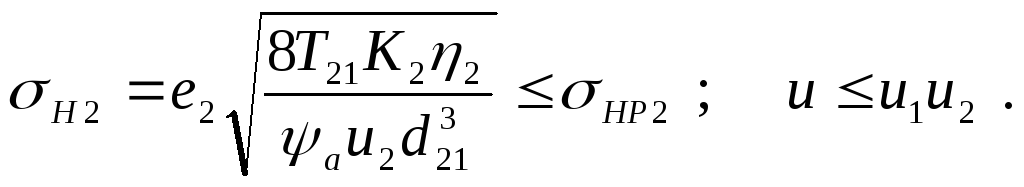
Так как d₂₁ = 2а₂/(1+ и₂), то, обозначив:

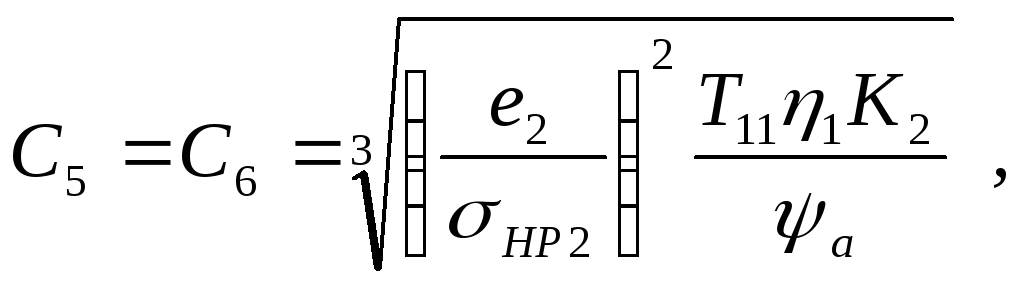С₇ = и,

получим следующие нелинейные ограничения в виде неравенств:

Таким образом, задача оптимизации двухступенчатого червячно-цилиндрического редуктора сведена к решению задачи геометрического программирования со степенью трудности задачи:

d = 7 – (4 + 1) = 2.

Соответствующая этой задаче двойственная программа состоит в максимизации двойственной функции:

где i = 1,2, . . . , 7;

k = 1, 2, 3.

В этих выражениях j = 0, 1, 2.

Условия неотрицательности на вектор r:

i = 1,2, . . . , 7.

Базисные постоянные находятся из выражения

j = 0, 1, 2,

где С_i > 0 – коэффициенты, зависящие от исходных данных.

Вектор нормализации b⁽⁰⁾ удовлетворяет условию соответственно нормализации и ортогональности:

j = 1, 2, 3, 4.

Векторы невязки b^(j) (j = 1, 2) образуют базис пространства решений однородной линейной системы:

j = 1, 2, 3, 4.

где а_ij – матрица экспонент исходной задачи геометрического программирования.

Векторы b⁽⁰⁾, b⁽¹⁾ и b⁽²⁾, найденные в результате преобразований матрицы экспонент по методу Бранда, имеют вид

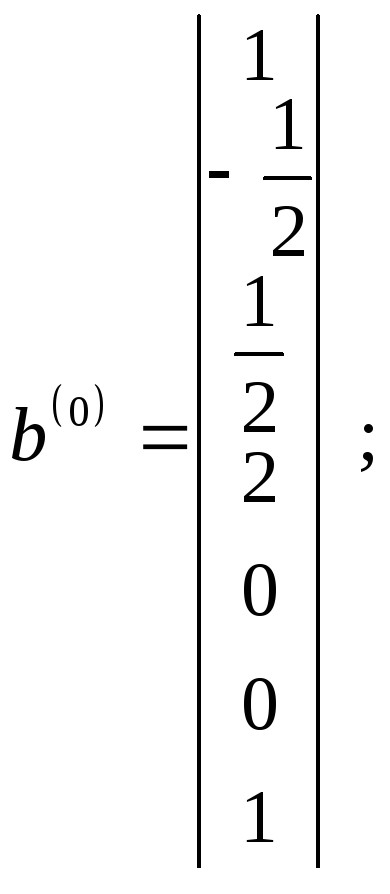
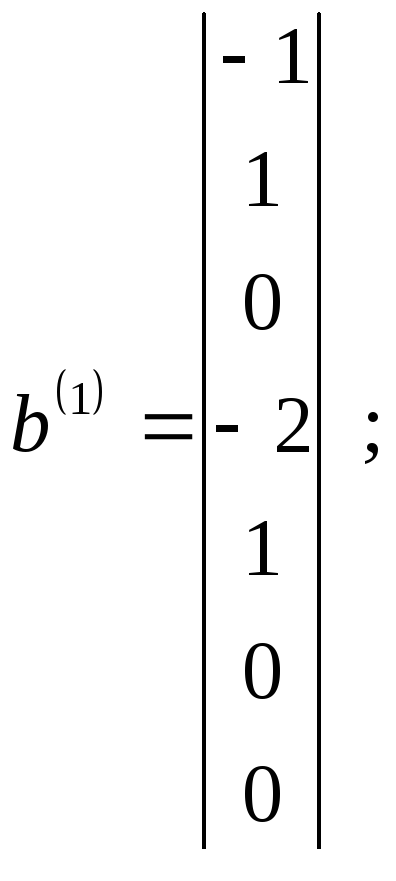
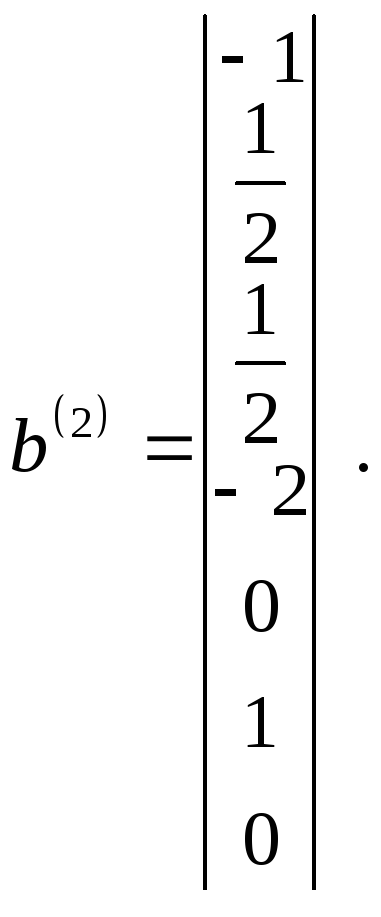
Несложно проверить, что полученные векторы нормализации и невязки удовлетворяют необходимым условиям.

Следовательно, двойственные переменные находятся по формулам

₁ = 1 – r₁ – r₂;

₂ = -0,5 + r₁ + 0,5r₂;

₃ = 0,5 + 0,5r₂;

₄ = 2 – 2r₁ – 2r₂;

₅ = r₁;

₆ = r₂; ₇ = 1.

Значения r₁ и r₂, максимизирующие двойственную функцию, определяются из решения системы

где базисные постоянные находятся по формулам

После определения максимизирующих значений r₁ и r₂ максимальное значение двойственной функции можно найти из выражения

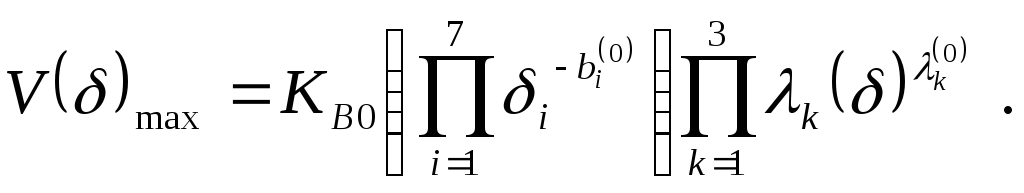
Это значение определяет одновременно и минимум ЦФ.

Оптимальные значения u₁, u₂, t и a₂ находятся из решения системы уравнений

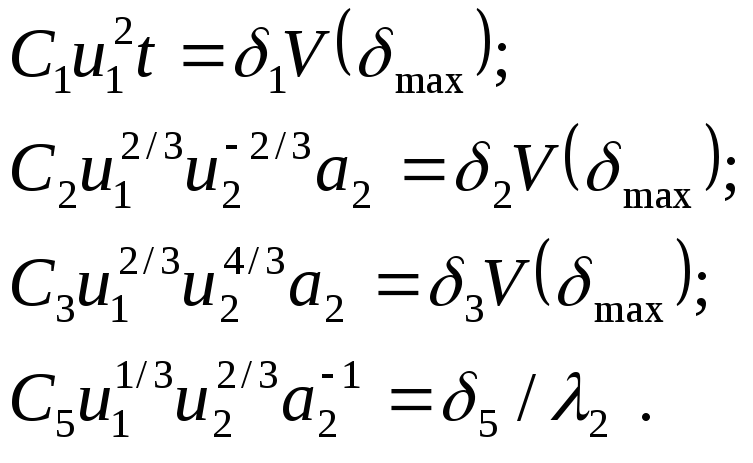
Решив эту систему, получим формулы для вычисления оптимизируемых параметров

Следует отметить, что аналогичный подход можно применить для многоступенчатых редукторов и других типов, когда из рекомендуемого диапазона передаточных чисел необходимо выбрать единственное решение, минимизирующее значение ЦФ.