2.6.1. Вариационное исчисление

В ряде задач для описания геометрических характеристик непрерывно изменяющихся поперечных сечений элемента конструкции механической системы требуется введение функций, задающих форму элемента. Для определения характерных свойств данного класса задач рассмотрим сначала два типичных примера.

x Рис. 2.1 Рис. 2.2

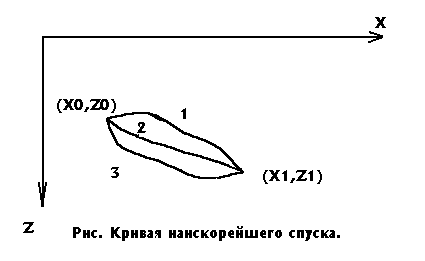
Пример 1. (рис.2.1) Требуется найти кратчайшую кривую между двумя точками (x0,z0) и (x1, z1) на плоскости X и Z. Любой кривой, соединяющей две заданные точки, сопоставляется ее длина. Задача состоит в том, чтобы выбрать кривую z(x), имеющую наименьшую длину. Для кривой z(x) длина определяется выражением f(x)= (1+()2)dx. Пример 2. (рис.2.2) В вертикальной плоскости заданы две точки (x0, z0) и (x1,z1), не лежащие на одной вертикальной прямой.Требуется найти соединяющую эти точки кривую, вдоль которой материальная точка, находившаяся в состоянии покоя в(x0,z0), будет скользить без трения в точку (x1,z1) за наименьшее время.

Пусть m - масса материальной точки, g - ускорение свободного падения. Так как тело начинает движение из состояния покоя (x₀, z₀), а трение отсутствует, то можно записать уравнение энергии в следующем виде:

mV²=mg(z-z₀),

где V - скорость, определяемая по формуле:

V=(()²+()²)^0,5=(1+()²)^0,5,

t - время движения материальной точки.

После преобразований представленных уравнений можно получить:

dt=(1+()²)^0,5dx/(2g(z-z₀))^0,5.

Следовательно, полное время , необходимое для перемещения из (x₀, z₀) в (x₁, z₁), рассчитывается по формуле:

.

Данное выражение показывает, что  зависит от вида всей кривой, по которой скользит материальная точка. Такая задача сводится к нахождению кривой z(x), называемой брахистохроной.

Из приведенных примеров видно, что функция, описывающая кривую, должна определяться из решения оптимизационной задачи. Кроме того, значения минимизируемых величин определяется функциями, задающими указанные кривые. Поэтому рассматриваемые величины являются функциями от функций. Они называются функционалами. Типичным функционалом, встречающимся в вариационном исчислении, является интеграл.

Итак, оптимизационная задача ставится следующим образом: найти в классе функций, интегрируемых вместе с квадратом производных и удовлетворяющих граничным условиям, такую функцию z(x) при x₀xx_1, которая минимизирует функционал f(x).

Приведенное обсуждение примеров 1 и 2 позволяет сформулировать основную задачу вариационного исчисления для более широкого класса задач. Найти дважды непрерывно дифференцируемую на интервале x₀ xx₁ функцию z(x), удовлетворяющую граничным условиям:

z_i (x₀)=z_i⁰ для некоторых 1in,

z_j(x₁)=z_j¹ для некоторых 1jn

и минимизирующую функционал:

f(z)=,

гдеF - дважды непрерывно дифференцируемая по всем своим аргументам действительнозначная функция, а z'= .

Указанные выше граничные условия означают, что кривые в примерах 1 и 2 проходят через заданные точки.

2.6.2. Частные случаи и примеры

В практических задачах вид функции позволяет упростить дифференциальное уравнение второго порядка для функцииz(x), необходимое для решения задачи вариационного исчисления. Такое уравнение называется уравнением Эйлера – Лагранжа и с использованием цепного правила дифференцирования сложной функции и обычных обозначений имеет вид

.

Случай 1. F зависит только от z^', поэтому F=F(z^').

Для задачи из примера 1 необходимо найти кратчайшую кривую в плоскости x-z, проходящую через точки (0, 0) и (1, 1). При этом исследуемая функция имеет вид F=(1+(z^')²)^1/2.

Следовательно, уравнение Эйлера-Лагранжа записывается в виде

(1+(z^')²)^-3/2z^"=0.

Так как (z^')² 0 , тоz^"=0, поэтому z=ax+b,

где a и b - константы.

Отсюда следует, что кривая, кратчайшим образом соединяющая две заданные точки, является прямой линией, что и неудивительно. Из граничных условий следует: z(0)=b=0, z(1)=a=1. Поэтому решением данной задачи является функция z(x)=x.

Случай 2. Пусть F зависит только от x и z^': F=F(x, z^'). В этом случае уравнение Эйлера–Лагранжа имеет вид

,

поэтому: F_z'(x, z^')=c, где с - произвольная постоянная.

Случай 3. Функция z - вещественная, а F зависит только от z и z^': F=F(z, z'). Уравнение Эйлера-Лагранжа в этом случае имеет вид

F_z- F_z'z z'- F_z'z' z"=0.

Умножение на z' приводит к уравнению

z' F_z-(z')²F_z'z- z'z"F_z'z'=0,

что сводится к d(F-z'F_z')/dx=0. Следовательно, F-z' F_{z '}=C, где С - произвольная постоянная.

Решим задачу о брахистохроне (пример 2).

Функция времени находится из выражения

,

где .

Уравнение из случая 3 записывается в виде

.

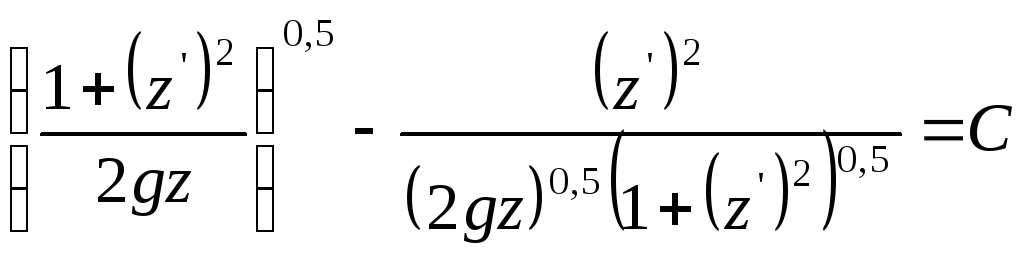Оно сводится к уравнению z(1+(z')²)=C₁, где С₁ - новая константа. Решение этого дифференциального уравнения представляет собой свойство циклоид, записанных в параметрическом виде:

x=C₂+C₁/2(S- sin S), z=C₂/2(1- cos S).

Константы С₁ и С₂ выбираются путем выделения соответствующей циклоиды, проходящей через заданные точки.

Изложенный подход, который иногда применяется совместно с одним из численных методов, например, с методом наискорейшего спуска, может явиться основой для создания вычислительных алгоритмов в решении статических и динамических задач проектирования элементов РК. К ним можно отнести следующие.

1. Колонна наименьшего веса, способная выдержать, например, заданную сжимающую нагрузку. Поскольку поперечное сечение определяется только переменными, определяющими ее форму, то задача сводится к исследованию функционала, т.е. к решению уравнения Эйлера-Лагранжа. Подобный алгоритм применим для колонн с различными граничными условиями и формой поперечного сечения.

2. Упругие системы (балки, пластины и другие силовые конструкции) переменной толщины, рассчитываемые на изгиб, колебания и устойчивость при наличии ограничений на напряжения, перемещения, собственные частоты колебаний и размеры конструкций.

3. Балки и пластины, к которым приложены динамические нагрузки. Несмотря на идеализацию при постановке указанных задач, получаемое решение для простых конструкций обладает характерными особенностями, применимыми и для сложных элементов РК.