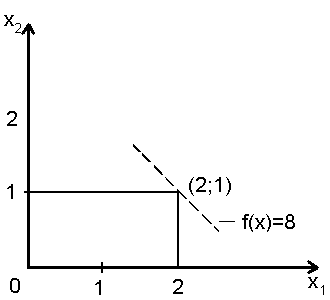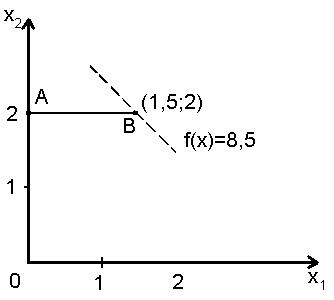3.2. Расчет конструктивных элементов ракет

3.2.1. Примеры решения вопросов по компоновке оборудования

Следующие примеры показывают возможность применения даже простых методов оптимизации для решения задач компоновки оборудования на ракете. В случае многофакторной оптимизации необходимо использовать метод целочисленного линейного программирования.

Пример 1.В шар радиусом R вписать прямой круговой конус максимального объема.

Решение

Обозначим: R-радиус шара; r - радиус основания конуса; - высота конуса, гдеx - расстояние от центра шара до основания конуса.

Используя очевидные соотношения, получим

; ;,

где V- объем конуса.

Следовательно, .

Экстремальные значения определяются из следующего выражения:

.

Решая квадратное уравнение, получим

,

т.е. ;.

.

Пример 2. Среди всех круговых конусов с данной образующей l найти корпус с наибольшим объемом.

Решение

Целевая функция имеет вид , гдеR – радиус основания конуса; h – высота конуса.

Учитывая соотношение: , можно записать

.

На основании :.

Следовательно, конус с ибудет иметь наибольший объем.

Пример 3. Определить размеры а, в и с параллелепипеда заданного объема V, который имел бы минимальную поверхность S.

Решение

Критерий оптимальности этой задачи (ЦФ) имеет вид

Ограничение на параметры a, b и c согласно условию задачи описывается выражением

Функция Лагранжа имеет вид

Следовательно:

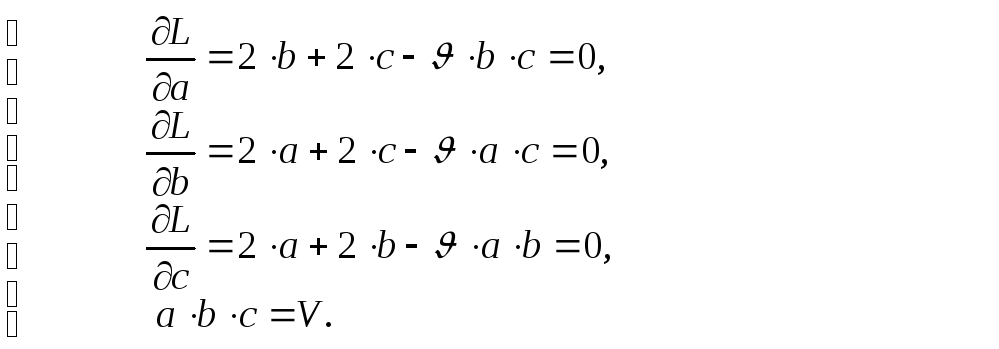
Для получения расчетных формул выполним следующие действия: разделим первое уравнение системы на второе и первое – на третье.

;,a=b;

;,a=c.

Следовательно: a³=V; a=b=c=, поэтому.

Пример 4. Разместить в приборном отсеке ракеты приборы двух типов, масса каждого 2 кг, но один из них трехфункциональный, а другой – двухфункциональный; при этом, учитывая ограничение по общей массе в 7 кг, добиться максимальной эффективности приборов.

Решение

Математическая формулировка задачи выглядит следующим образом.

Максимизировать ЦФ

при ограничениях ;;,

где - целочисленные.

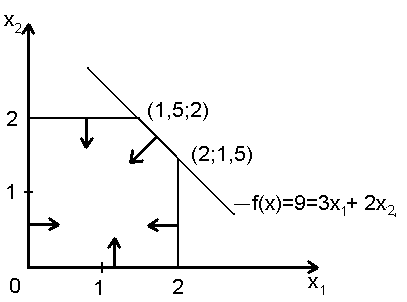
Начальный шаг решения этой задачи состоит в нахождении решения задачи линейного программирования (ЛП), получаемой при отбрасывании условий целочисленности и. Обозначим эту задачу через ЛП-1, решение которой представлено на рис. 3.10.

Рис. 3.10. Решение ЛП – 1

Из полученного графика видно, что найденное решение (x1 = 2; x2 = 1,5; f(x) = 9) не может быть оптимальным, целочисленным . Данное значение представляет собой верхнюю границу истинного оптимального целочислен-ного значения, поскольку при выполнении условия целочисленностизначениеможет только уменьшиться.

Следующий шаг метода заключается в просмотре целочисленных значений , больших или меньших 1,5. Это делается путём добавления к задаче ЛП-1 ограничения либо, либо. Таким образом, из задачи ЛП-1 получаются две задачи следующего вида: ЛП-2 и ЛП-3, представленные соответственно на рис. 3.11 и 3.12.

Рис. 3.11. Решение ЛП – 2

Рис. 3.12. Решение ЛП – 3

В этих задачах наряду с первоначальным условием соответственно добавлены:

- для ЛП – 2 новое ограничение ,

- для ЛП – 3 новое ограничение , поэтому допустимая область в этом случае представляет собой просто отрезок АВ.

Изображённые допустимые области задач ЛП-2 и ЛП-3 обладают следующими свойствами.

1. Оптимальное решение задачи ЛП-1недопустимо для обеих задач ЛП-2 и ЛП-3. Таким образом, это решение не повторится.

2. Любое целочисленное (допустимое) решение исходной задачи допустимо для задачи ЛП-2 или ЛП-3. Таким образом, при введении этих задач не происходит потери допустимых (целочисленных) решений исходной задачи.

Оптимальное решение задачи ЛП-2 – точка (,), где. Следовательно, значениепредставляет собой нижнюю границу максимального значениядля смешанной задачи ЦЛП. Поскольку ранее была получена лишь верхняя граница, равная 9, нельзя утверждать, что решение ЛП-2 оптимально для исходной задачи. Следовательно, необходимо рассмотреть задачу ЛП-3. Однако её решение недопустимо для исходной задачи ЦЛП, поскольку, но при этом. Поэтому необходимо проверить существование в допустимой области ЛП-3 целочисленного решения, дающего значение. Для этого рассматриваются задачи ЛП-4 и ЛП-5, получающиеся при добавлении к ЛП-3 ограниченийисоответственно.

Рис. 3.13. Решение ЛП – 4

Допустимая область задачи ЛП-4 состоит из отрезка ДС, показанного на рис. 3.13, задача ЛП-5 не имеет допустимых решений. Итак, точка (,) из задачи ЛП-2 представляет собой оптимальное целочисленное решение исходной задачи, так как, т.е. большеиз ЛП-4.

Удобно представить последовательность задач ЛП, возникающих при использовании процедуры метода ветвей и границ, в виде сети или дерева (рис. 3.14). Они состоят из множества вершин и соединяющих их дуг или ветвей. Каждая вершина представляет собой либо начальную, либо конечную точку некоторой ветви.

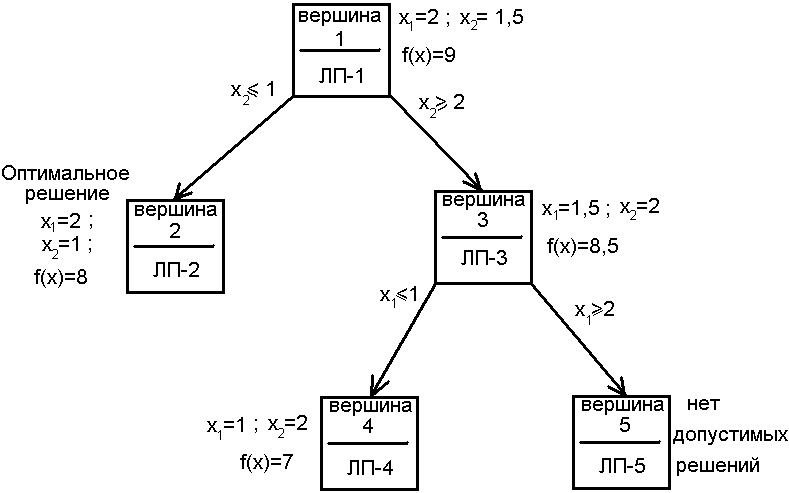
Рис. 3.14. Схема решения

Вершина 1 соответствует задаче ЛП-1, получаемой из исходной задачи при отбрасывании требования целочисленности переменных. Ветвление в вершине 1, определённое целочисленной переменной с помощью ограничения, приводит к вершине 2 (ЛП-2). Поскольку задача ЛП-2 имеет оптимальное целочисленное решение, нет необходимости производить ветвление в вершине 2. В этом случае, когда в некоторой вершине возникает подобная ситуация, говорят, что рассматриваемая вершина прозондирована. Ветвление в вершине 1 по ограничениюдаёт ЛП-3 (вершина 3). Поскольку оптимальное решение ЛП-3 является дробным, происходит дальнейшее ветвление в вершине 3 по целочисленной переменной. Таким образом, появляются вершины 4 и 5. Эти вершины являются прозондированными, поскольку ЛП-4 обладает целочисленным решением, а ЛП-5 не имеет допустимых решений. Наилучшее решение из прозондированных в вершинах является оптимальным.