
- •В.А. Панов математические основы теории систем. Методы оптимизации
- •Содержание
- •1. Основные понятия и определения 6
- •2. Линейное программирование 13
- •3. Нелинейное программирование 53
- •4. Вариационное исчисление 91
- •5. Оптимальное управление 109
- •Введение
- •1. Основные понятия и определения
- •1.1. Оптимизационная задача
- •1.2. Допустимое решение
- •1.6.1. Частные критерии
- •1.6.2. Обобщенные критерии
- •Обобщенный аддитивный критерий
- •Обобщенный мультипликативный критерий
- •1.6.3. Минимаксные критерии
- •1.7. Общая характеристика методов поиска экстремума
- •Краткая характеристика методов и задач
- •2. Линейное программирование
- •2.1. Стандартный вид задачи линейного программирования (злп)
- •2.2. Способы приведения задачи линейного программирования к стандартному виду
- •2.3. Графический метод решения задач линейного программирования
- •2.4. Симплекс-метод решения задач линейного программирования
- •2.4.1. Канонический вид злп
- •2.4.2. Симплекс-таблица, соответствующая каноническому виду
- •2.4.3. Нахождение координат вершины допустимого многогранника по каноническому виду (симплекс-таблице)
- •2.4.4. Алгоритм решения злп с помощью симплекс-метода
- •Задание для самостоятельной работы
- •2.5. Приведение злп к каноническому виду
- •2.5.1. Метод искусственного базиса
- •2.6. Алгоритм двойственного симплекс-метода
- •Задания для самостоятельной работы
- •2.7. Целочисленное линейное программирование
- •2.7.1. Метод сечения Гомори
- •2.8. Транспортная задача
- •2.8.1. Постановка задачи
- •2.8.2. Математическое описание задачи
- •2.8.3. Транспортная таблица
- •2.8.4. Таблица издержек
- •2.8.5. Метод «северо-западного» угла
- •2.8.6. Алгоритм решения транспортной задачи
- •Задания для самостоятельной работы
- •3. Нелинейное программирование
- •3.1.2.2 Метод ненаправленного поиска
- •3.1.2.3. Метод дихотомии (деление отрезка пополам)
- •3.1.2.4. Метод «золотого сечения»
- •3.1.2.5. Метод Фибоначчи
- •Задание для самостоятельного решения
- •3.2. Графический метод решения задач нелинейного программирования
- •Целевая функция линейная, ограничения нелинейны
- •Ограничения линейные, целевая функция нелинейна
- •3.3. Задачи дробно-линейного программирования
- •Задания для самостоятельного решения
- •3.4. Методы поиска безусловного экстремума функции многих переменных
- •3.4.1. Аналитический метод
- •3.4.2. Итерационные методы
- •3.4.2.1. Метод покоординатного спуска
- •3.4.2.2. Метод наискорейшего спуска
- •Задания для самостоятельной работы
- •3.5. Решение задач нелинейного программирования с ограничениями-равенствами
- •Метод неопределенных множителей Лагранжа
- •Задание для самостоятельной работы
- •3.6. Задачи квадратичного программирования
- •Задания для самостоятельной работы
- •3.7. Метод условного градиента
- •5. X1, x2,xn 0. (3.25)
- •X1, x2,xn 0.
- •Задания для самостоятельной работы
- •3.8. Метод штрафных функций
- •4. Вариационное исчисление
- •4.1. Формула Эйлера-Лагранжа
- •4.2. Частные случаи формулы Эйлера
- •4.3. Обобщенная задача вариационного исчисления
- •4.4. Решение задач вариационного исчисления с ограничениями
- •4.5. Изопериметрическая задача
- •4.6. Функционалы, зависящие от производных высших порядков
- •Задание для самостоятельного решения
- •5. Оптимальное управление
- •5.1. Постановка задачи
- •5.2. Классификация задач оптимального управления
- •5.3. Принцип максимума Понтрягина
- •5.4. Задача о максимальном быстродействии
- •Задания для самостоятельного решения
- •Список литературы
- •Основы теории оптимизации в.А. Панов
1.2. Допустимое решение

Допустимое решение – это множество значений переменных, удовлетворяющих ограничениям. Допустимые значения образуют некоторую область – область допустимых решений. Оптимальное решение находится в этой области. Например, для двумерной задачи область допустимых решений образует выпуклый многогранник (рис. 1.1). Здесь x1, x2 – параметры, по которым проводится оптимизация.
1.3. Локальный экстремум

Локальный экстремум – это минимальное или максимальное значение функции в окрестности некоторой точки (рис. 1.2). Здесь x0 – локальный минимум (окрестность т. А), x1 – локальный максимум (окрестность т. В).
1.4. Глобальный экстремум
Глобальный экстремум – минимальный из всех локальных минимумов или максимальный из всех локальных максимумов.
В этом курсе под понятием минимума (максимума) будет пониматься минимальное (максимальное) значение функции на заданном отрезке (рис. 1.3).
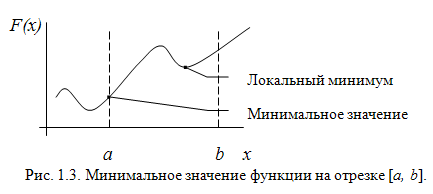
Рис. 1.3. Минимальное значение функции на отрезке [a, b]
1.5. Условный и безусловный экстремум
Условный экстремум – экстремум, удовлетворяющий ограничениям.
Безусловный экстремум – экстремум, на который не накладываются ограничения.
Пример задачи на поиск безусловного экстремума: найти минимум функции
![]()
Добавив к этой постановке задачи ограничения, получим задачу на поиск условного экстремума:
![]()
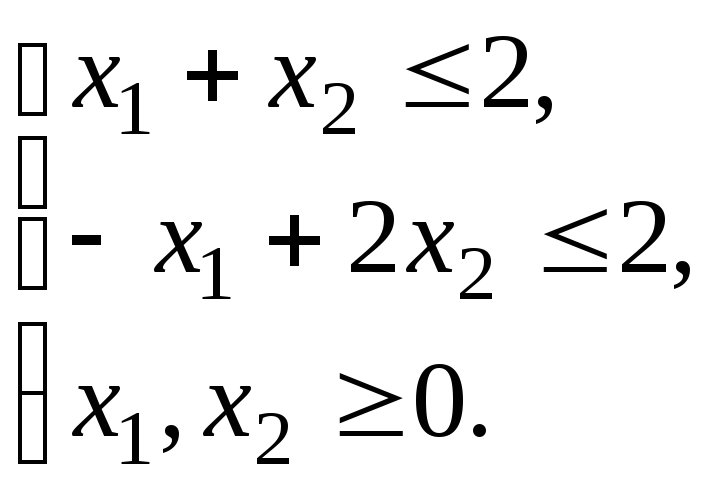
1.6. Критерии оптимальности
Критерий оптимальности – это выражение, характеризующее качество объекта.
Выбор критерия оптимальности является сложной задачей. Рассмотрим задачу выбора критерия оптимальности на примере оптимизации параметров микросхемы.
Основные параметры микросхемы:
Р – потребляемая мощность;
tз – время задержки распространения сигнала (быстродействие);
U – максимально допустимая амплитуда помехи (помехоустойчивость).
Требуется оптимизировать микросхему по этим параметрам.
Критерии оптимальности подразделяют на три группы: частные, обобщенные и минимаксные.
1.6.1. Частные критерии
Частные критерии оптимальности делятся на две подгруппы:
оптимизация по какому-либо одному параметру (например, минимальная потребляемая мощность, Р min);
минимизация отклонения реальной характеристики от теоретической (рис. 1.4)
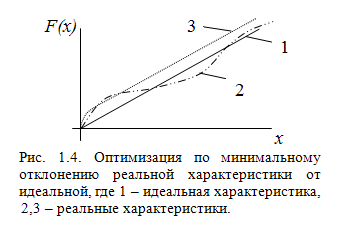
Необходимо
найти такой вектор внутренних параметров
![]() ,
при котором отклонение реальной
характеристики от идеальной будет
минимальным. На характеристике выбирают
n
точек, находят в этих точках разности
между реальной и идеальной характеристиками:
,
при котором отклонение реальной
характеристики от идеальной будет
минимальным. На характеристике выбирают
n
точек, находят в этих точках разности
между реальной и идеальной характеристиками:
![]() (1.3)
(1.3)
Затем разности усредняются:
![]() (1.4)
(1.4)
где Q – критерий отклонения, Ci – весовые коэффициенты.
1.6.2. Обобщенные критерии
Обобщенные критерии – это критерии, связывающие несколько параметров объекта. Обобщенные критерии подразделяются на две подгруппы: обобщенные аддитивные и обобщенные мультипликативные критерии.
Обобщенный аддитивный критерий
В выражение этого критерия входит сумма выходных параметров объекта, взятая с весовыми коэффициентами
![]() (1.5)
(1.5)
где![]() – выходные параметры объекта,
– выходные параметры объекта,![]() – весовые
коэффициенты,
– весовые
коэффициенты,
![]() – вектор внутренних параметров.
– вектор внутренних параметров.
Для цифровой микросхемы выходными параметрами являются потребляемая мощность (Р), помехоустойчивость (U) и быстродействие (tз). Причем, потребляемую мощность и время задержки распространения сигнала требуется по возможности уменьшить, а максимальную амплитуду помехи – увеличить. Следовательно, критерий оптимальности будет иметь вид
![]() (1.6)
(1.6)
