Задания для самостоятельного решения

1. 2.

x₁ + 2x₂ ≤ 16, –x₁ + x ₂ + 3x₃ = 8,

x₁ + x₂ ≤ 10, 2x₁ – x₂ – x₃ = 4,

x₁ ≤ 6, x_j ≥ 0, j = 1, 2, 3.

x₂ ≤ 7,

x₁, x₂ ≥ 0

3. 4.

x₁ – x₂ + 2x₃ = 4, x₁ + x ₂ + x₅ = 3,

–x₁ + 2x₂ + x₃ + x₄ = 6, 3x₁ + x₂ – x₃ = 4,

x_j ≥ 0, j = 1,..4. –x₁ + 3x₂ + x₄ = 6,

x_j ≥ 0, j = 1,..5.

5.

6x₁ – 3x ₂ + x₃ + x₄ = 12, x₁ + x ₂ + x₃ = 6,

7x₁ – x₂ + 2x₃ ≤ 12, 3x₁ – 2x₂ + x₄ = 9,

–4x₁ + 2x₂ – x₃ – x₅ = 1, –x₁ + 2x₂ + x₅ = 10,

x_j ≥ 0, j = 1,..5. x_j ≥ 0, j = 1,..5.

7.

4x₁ – x ₂ ≤ 5, –x₁ + 3x ₂ – x₄ = 10,

x₁ + 3x₂ – x₃ = 7, 2x₁ + 4x₂ – x₃ – x₄ = 20,

–3x₁ + 4x₂ + x₄ = 17, 5x₁ + 2x₂ + x₅ = 35,

x_j ≥ 0, j = 1,..4. –3x₁ + 2x₂ + x₆ = 11,

x_j ≥ 0, j = 1,.6.

9.

x₁ + x ₂ – x₃ = 5,

–x₁ + 2x₂ ≥ 1,

–3x₁ + x₂ + x₄ = 1,

x_j ≥ 0, j = 1,...,4.

3.4. Методы поиска безусловного экстремума функции многих переменных

В задачах на поиск безусловного экстремума отсутствуют ограничения.

3.4.1. Аналитический метод

Задана функция нескольких переменных f(х₁, х₂х_n)  min (max).Требуется найти такие вектора при которых функция минимальна.

Алгоритм.

1. Находим частные производные и приравниваем их нулю:

, (3.12)

Решаем полученную систему (3.12).

2. В результате решения находим вектора .

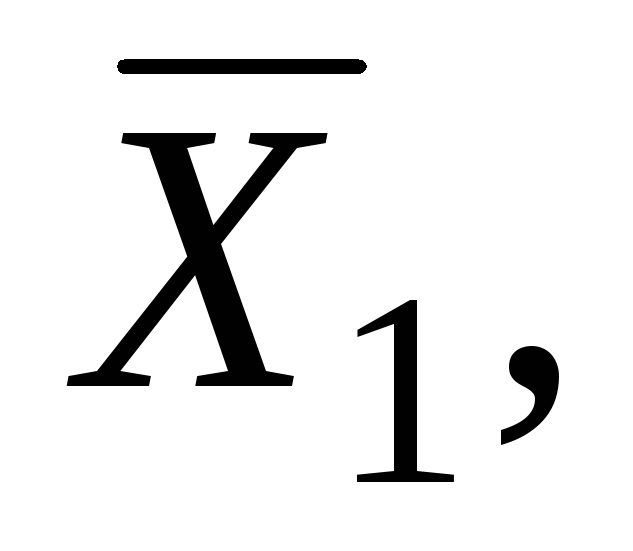
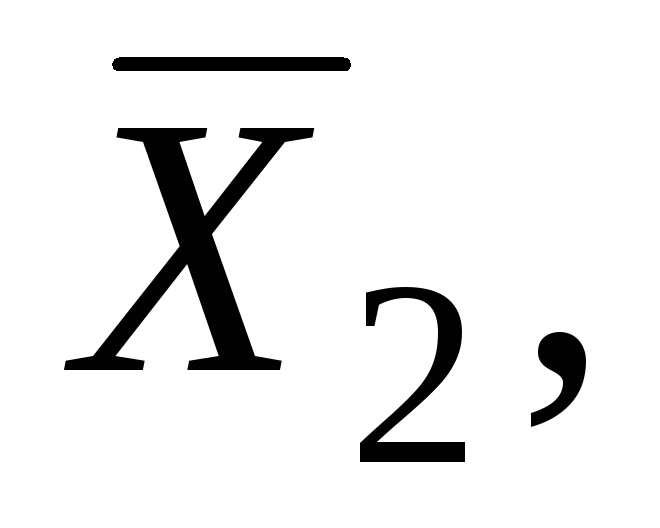
3. Определение типа экстремума.

Для определения типа экстремума для каждой точки составляется матрицаА следующего типа:

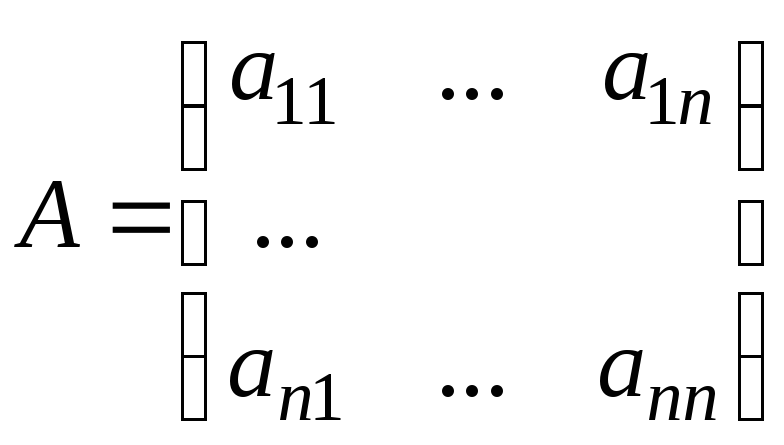, где (3.13)

Тип экстремума находится из следующего положения.

Если все главные миноры матрицы А, найденные для точки , положительны, то функция в этой точке имеет минимум.

Если все главные миноры матрицы (–А), найденные для точки , положительны, то функция в этой точке имеет максимум.

Во всех остальных случаях функция в точке , экстремума не имеет.

Главный минор _i – это определитель подматрицы, получающейся из исходной путем отчеркивания i-ой строки и i-го столбца.

Пример.

F(x,y) = 3x³ – x + y³ – 3y² – 1 .

Найти экстремумы заданной функции.

Решение.

1. 

2. 

3. Для определения типа экстремума требуется рассмотреть четыре точки:

(1/3, 0), (–1/3, 0),(1/3, 2),(–1/3, 2).

,

, ,

, .

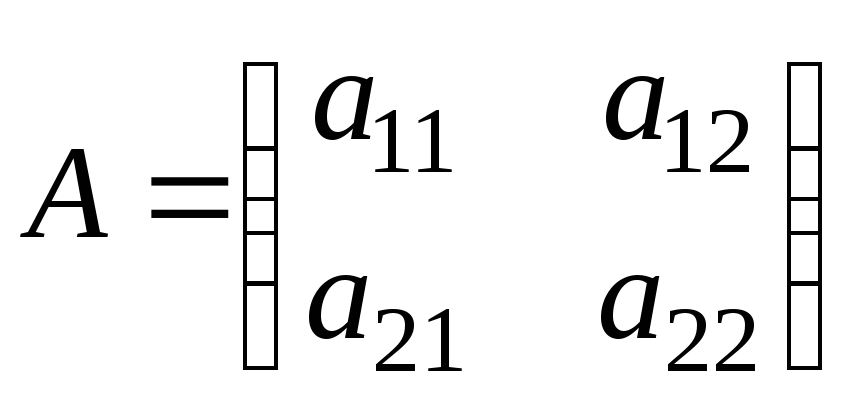Для точки (1/3, 0):

а₁₁ = 6, а₁₂ = а₂₁ = 0, а₂₂ = –6

₁ () =а₁₁ = 6  0, ₂ () =а₁₁ а₂₂ – а₁₂ а₂₁ = –36  0,

₁ (–) = –а₁₁ = –6  0, ₂ (–) =а₁₁ а₂₂ – а₁₂ а₂₁ = –36 0,

Следовательно, в точке нет ни минимума, ни максимума.

Для точки (–1/3, 0):

а₁₁ = –6, а₁₂ = а₂₁ = 0, а₂₂ = –6

₁ () =а₁₁ = –6  0, ₂ () =а₁₁ а₂₂ – а₁₂ а₂₁ = 36  0,

₁ (–) = –а₁₁ = 6  0, ₂ (–) =а₁₁ а₂₂ – а₁₂ а₂₁ = 36 0,

Следовательно, в точке функция имеет максимум.

Аналогично анализируются точки и .

3.4.2. Итерационные методы

Постановка задачи:

Дано:

1. Функция нескольких переменных f(х₁, х₂х_n)  min (max).

2. Точка 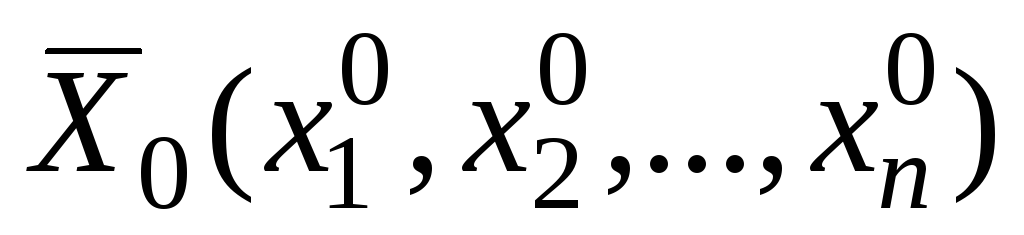– начальное приближение к экстремуму.

3.  – точность нахождения экстремума.

Критерий окончания счета.

Обычно используются два критерия окончания счета:

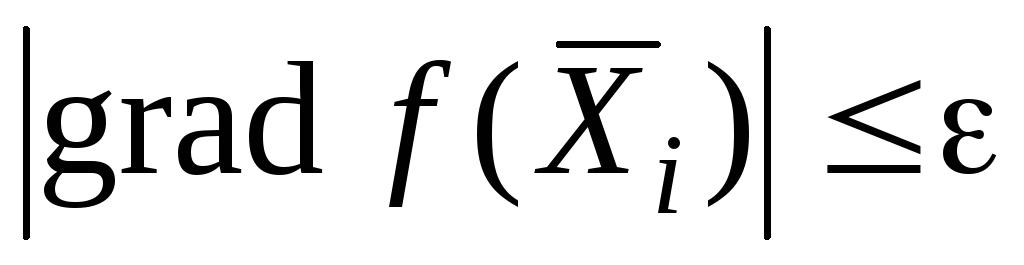1. (3.14)

Модуль градиента в точке экстремума равен нулю. Следовательно, чем меньше модуль градиента, тем ближе к экстремуму точка. Модуль градиента:

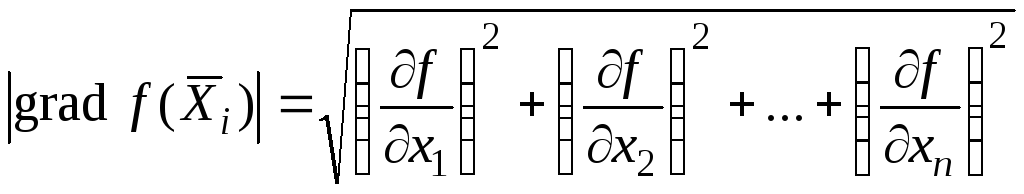
2. (3.15)

Разность значений функции в двух соседних точках при приближении к экстремуму стремится к нулю.