4.6. Функционалы, зависящие от производных высших порядков
Постановка задачи:
граничные условия: y(x0) = y00, y(x1) = y10,
y(x0) = y01, y(x1) = y11, (4.27)
y(n–1)(x0) = y0 n–1, y(п–1)(x1) = y1 n –1.
Найти: функцию у(х), доставляющую экстремум функционалу.
Поиск решения будем вести на примере следующей задачи:
y(x0) = y00, y(x1) = y10, y(x0) = y01, y(x1) = y11.
Предположим, что экстремум функционала достигается при функции у(х). Дадим функции у(х) приращение у, тогда у получит приращение у, у – приращение у.
Наложим условие у = у = 0 в точках х0 и х1. Далее, аналогично функционалам, зависящим от производных первого порядка; найдем главное приращение функционала:
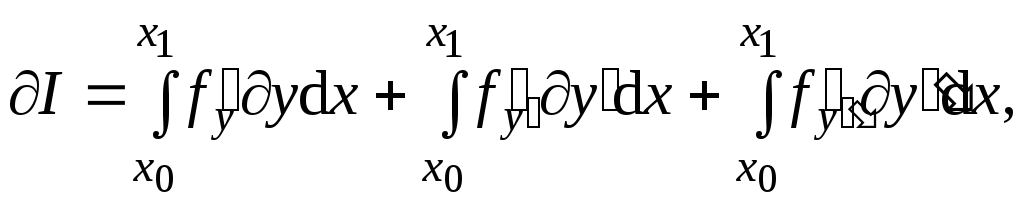
исходя
из (4.5).
Проинтегрируем
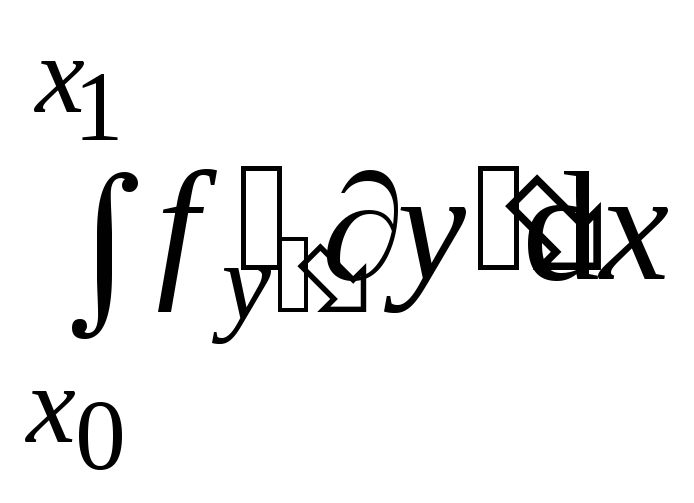по частям:
fy y = 0, так как y = 0 в точках х0 и х1.
Последнее выражение также проинтегрируем по частям.
fy y = 0, так как y = 0 в точках х0 и х1.
Таким
образом,
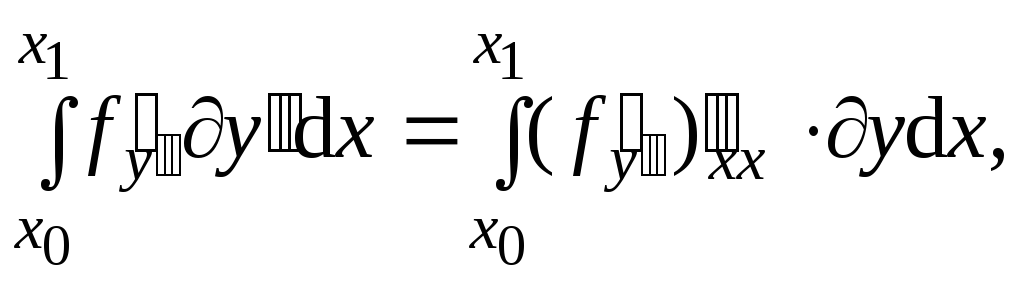
На функции, доставляющей экстремум функционалу:
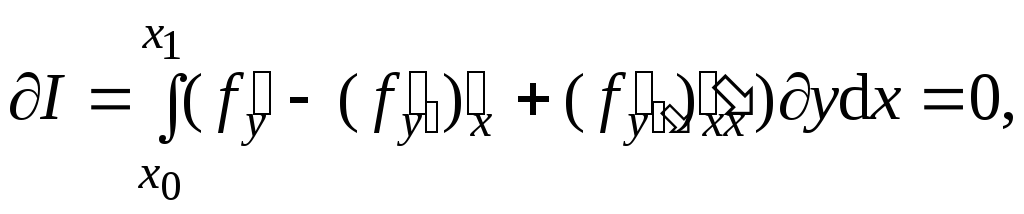
Так как у ≠ 0, то fy – (fy )x +(fy)xx = 0.
Последнее выражение есть формула Эйлера-Пуассона для старшей степени производной 2.
Если функционал зависит от производной n-ой степени, то формула Эйлера-Пуассона примет следующий вид:
(4.28)
Условия Лежандра для определения типа экстремума:
если на интервале интегрирования
,
то у(х)
доставляет максимум функционалу,
,
то у(х)
доставляет минимум функционалу,
,
то требуются дополнительные исследования
на экстремум.
Пример 1.
Решение.
Запишем уравнение Эйлера-Пуассона:
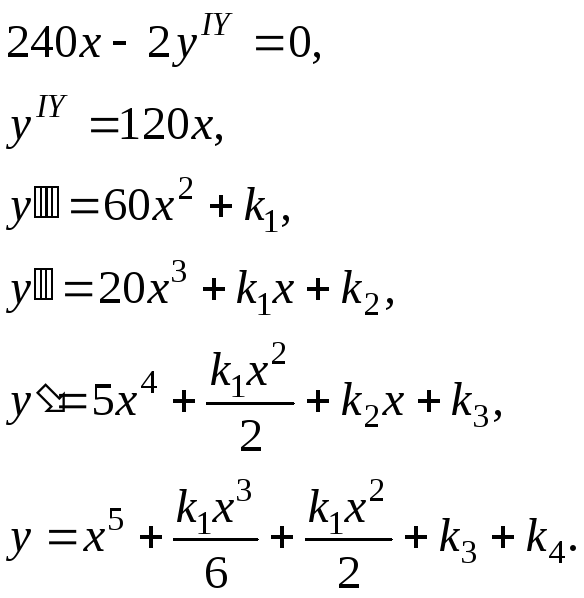
Подставив в эти выражения граничные условия, получим искомую функцию y = x5 + x3 – x2.
Определение
типа экстремума:
следовательно, найденная функция
доставляет функционалу максимум.
Пример 2.
Найти форму прогиба балки из условия минимума потенциальной энергии:
Решение.
1.
отсюда
2. Из начальных условий находятся константы:
3. Подставляются значения констант в функцию и получим:
Задание для самостоятельного решения
Дано:
– функционал, зависящий от функции, ее производной и аргумента функции;
– граничные условия;
– ограничения в виде определенного интеграла (в некоторых вариантах не задаются).
Требуется: решить задачу вариационного исчисления, то есть найти функцию, удовлетворяющую ограничениям и граничным условиям.
Методические указания
1. Для нахождения решения задачи вариационного исчисления использовать формулу Эйлера-Лагранжа.
2. Если в условие задачи в качестве ограничения входит определенный интеграл (изопериметрическая задача), то сначала составляется функция Лагранжа, которая затем подставляется в уравнение Эйлера-Лагранжа.
3. В изопериметрической задаче для нахождения постоянных интегрирования следует использовать граничные условия и ограничения в виде определенного интеграла.
4. Обозначения в задании:
x(t) – функция, которую требуется найти; t – аргумент;
1.
экстр.
.
2.
экстр.
.
3.
экстр.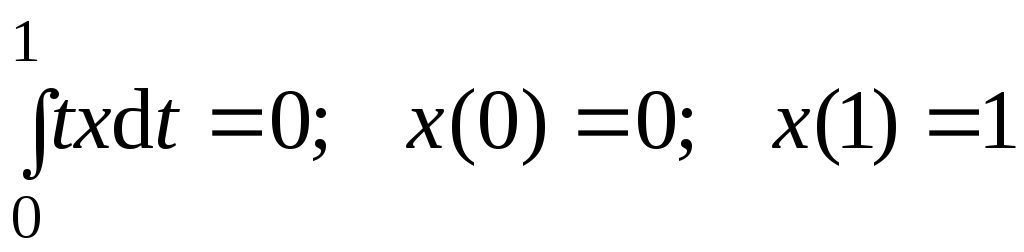
.
4.
экстр.
.
5.
экстр.
.
6.
экстр.
.
7.
экстр.
.
8.
экстр.
.
9.
экстр.
.
10.
экстр.
.
11.
экстр.
.
12.
экстр.
.
13.
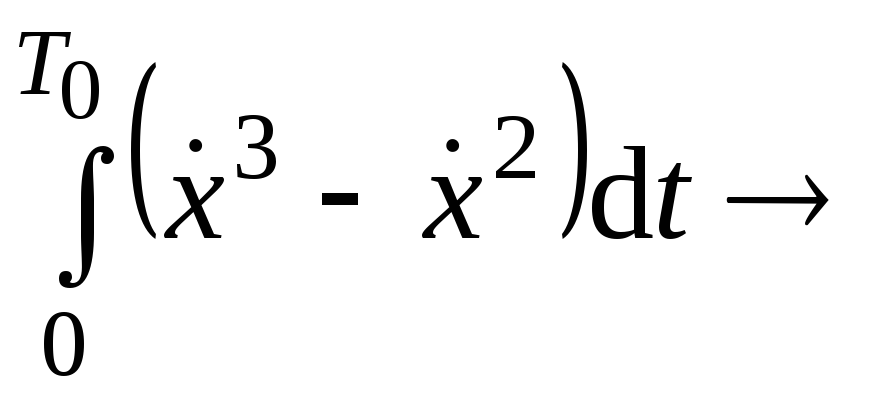экстр.
.
14.
экстр.
.
15.
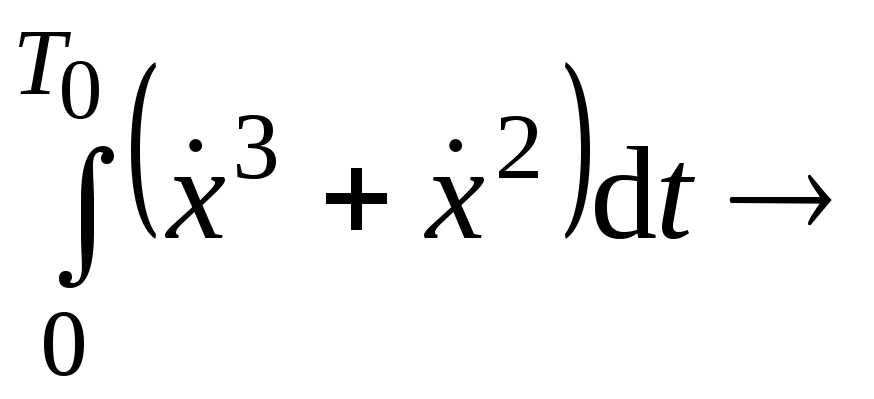экстр.
.
16.
экстр.
.
17.
экстр.
.
18.
экстр.
.
19.
экстр.
.
20.
экстр.
.