Задания для самостоятельной работы

Решить задачи нелинейного программирования методом условного градиента.

Дано: ε = 0,05, x^o = (0; 0).

1. f(x) = x₁² + 2x₂² – 16x₁ – 20 x₂ → min, 2. f(x) = x₁²+x₂²–18x₁–20x₂→min,

2x₁ + 5x₂ ≤ 40, x₁ + x₂ ≤ 15,

2x₁ + x₂ ≤ 16, 2x₁ + 5x₂ ≤ 60,

x₁, x₂ ≥ 0 3x₁ + x₂ ≤ 30,

x₁, x₂ ≥ 0

3. f(x) = (x₁ – 16) ² + (x₂ – 9)² → min, 4. f(x) = x₁² + x₂² – x₁x₂ – 3x₂→min,

5x₁ + 2x₂ ≤ 60, x₁ + x₂ ≤ 4,

x₁ + x₂ ≤ 15, x₁, x₂ ≥ 0

x₁ + 4x₂ ≤ 40,

x₁, x₂ ≥ 0

5. f(x) = x₁² + x₂² – 4x₁ – 8x₂ → min, 6. f(x) = x₁²+ 2x₁ – x₂→min,

6x₁ + 11x₂ + x₃ + 2x₄ = 96, x₁ + x₂ ≤ 15,

–2x₁ + 3x₂ – 2x₃ + x₄ = 8, x₁ + 3x₂ + x₃ = 30,

x₁, x₂, x₃, x₄ ≥ 0 5x₁ + 3x₂ + x₄ = 60,

x₁, x₂, x₃, x₄ ≥ 0

7. f(x) = x₁² + 2x₂² – 6x₁ – 32x₂ → min, 8. f(x) = 2x₁² + 3x₁ + 2x₂ + x₃ →min,

3x₁ + x₂ + x₃ = 30, x₁ + 3x₂ + 2x₃ ≤ 15,

x₁ + x₂ + x₄ = 15, 3x₁ + x₂ + x₃ ≤ 20,

2x₁ + 5x₂ + x₅ = 60, x₁, x₂, x₃ ≥ 0

x₁, x₂, x₃, x₄, x₅ ≥ 0

9. f(x) = x₁² + x₂² + x₃² + x₁ – 2x₂ → min 10. f(x) = x₁²–2x₁ +2x₂ +x₃ →min,

x₁ + 2x₂ + 3x₃ ≤ 18, x₁ + 3x₂ + 2x₃ ≤ 7,

2x₁ + x₂ + x₃ ≤ 20, 3x₁ + x₂ + x₃ ≤ 3,

x₁, x₂, x₃ ≥ 0 x₁, x₂, x₃ ≥ 0

3.8. Метод штрафных функций

Постановка задачи.

1. f(x₁, x₂,x_n)  min(max),

2.g_i(x₁, x₂,x_n)  0, i = 1, m (3.29)

3. = (x₁⁰, x₂⁰,x_n ⁰) – начальная точка приближения к экстремуму,

4.  – точность нахождения экстремума,

5. x₁, x₂,x_n  0, и целевая функция, и ограничения – многочлены любой степени, т.е. данный метод является универсальным, для решения задач нелинейного программирования.

Суть метода.

Вводится искусственная целевая функция F = f(x₁, x₂,x_n) + H(x₁, x₂,x_n).

Н – штрафная функция, определенная следующим образом (для определенности ищется минимум целевой функции):

Н = 0 внутри области допустимых решений,

Н > 0 вне области допустимых решений.

Вследствие такого задания Н безусловный экстремум функции F совпадет с условным экстремумом функции f.

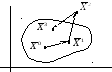
Рис. 3.7. Графическая иллюстрация метода штрафных функций.

В точках иН = 0. В точке Н  0, следовательно, значение F резко увеличится. Но поскольку функцию F требуется минимизировать, то следующая итерация возвращает текущую точку в область допустимых решений.

Выбор штрафной функции.

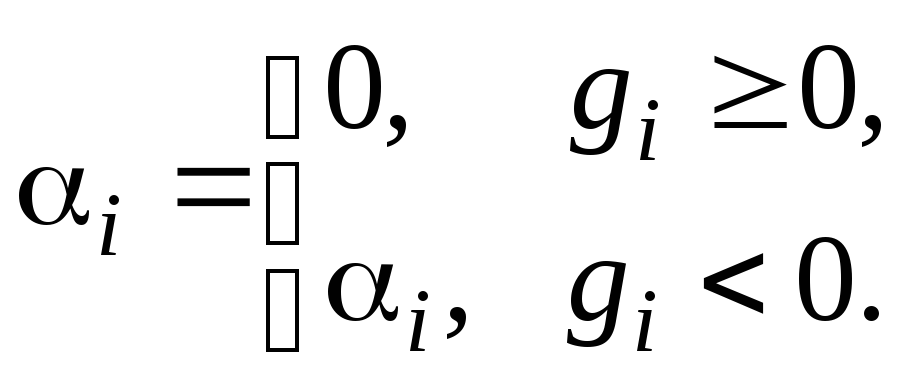(3.30)

Безусловный экстремум функции F находится любым известным методом.

Пример.

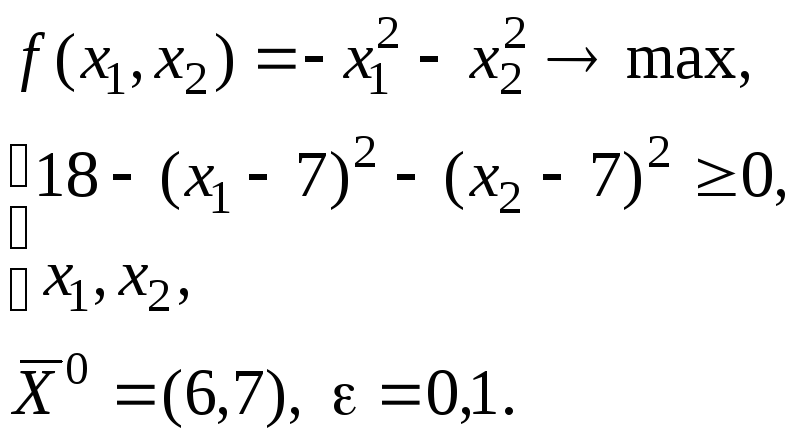
Решение.

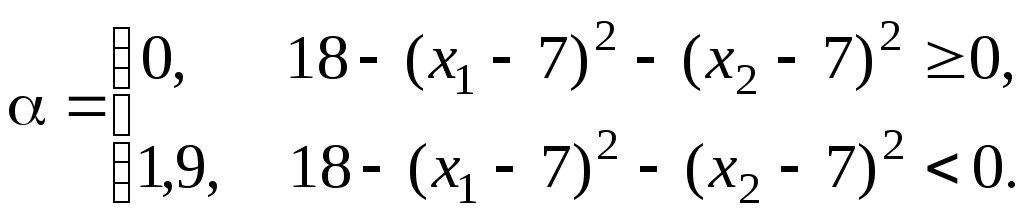
(Шаг выбран произвольным, но в данной задаче он больше нуля, так как интегральная функция H = ·g должна уменьшать ЦФ за областью допустимых решений).

Для простоты шаг в направлении градиента возьмем постоянным  = 0,1.

= (6, 7) , проверим выполнение ограничения для этой точки:

g(6, 7) > 0, следовательно,  = 0,

И т.д. пока не будет достигнута заданная точность (точность определяется как в задачах на безусловный экстремум).

4. Вариационное исчисление

Вариационное исчисление – это математическая дисциплина, занимающаяся поиском экстремума функционалов [5].

Функционал – выражение, зависящее от функции (например, определенный интеграл).

Пример.

Даны две точки на плоскости. Требуется соединить их такой кривой, чтобы круглое материальное тело (шар), двигаясь по этой кривой под действием силы тяжести без трения, доходило от одной точки до другой за минимальное время.

Составим математическое описание задачи:

Изменение кинетической энергии тела равно работе силы тяжести:

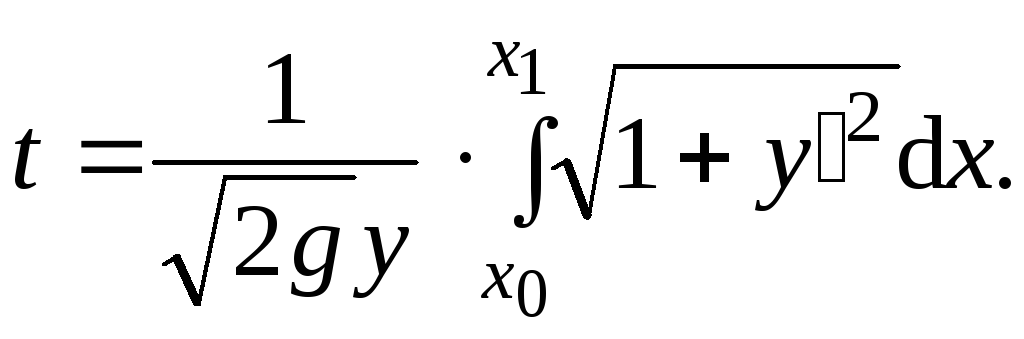
Ищем некоторую функцию у(х). Этой функции будет поставлено в соответствие некоторое число значение t для этой функции:

Задача – найти такую функцию у(х), при которой функционал (значение t) достигает минимума.