
- •В.А. Панов математические основы теории систем. Методы оптимизации
- •Содержание
- •1. Основные понятия и определения 6
- •2. Линейное программирование 13
- •3. Нелинейное программирование 53
- •4. Вариационное исчисление 91
- •5. Оптимальное управление 109
- •Введение
- •1. Основные понятия и определения
- •1.1. Оптимизационная задача
- •1.2. Допустимое решение
- •1.6.1. Частные критерии
- •1.6.2. Обобщенные критерии
- •Обобщенный аддитивный критерий
- •Обобщенный мультипликативный критерий
- •1.6.3. Минимаксные критерии
- •1.7. Общая характеристика методов поиска экстремума
- •Краткая характеристика методов и задач
- •2. Линейное программирование
- •2.1. Стандартный вид задачи линейного программирования (злп)
- •2.2. Способы приведения задачи линейного программирования к стандартному виду
- •2.3. Графический метод решения задач линейного программирования
- •2.4. Симплекс-метод решения задач линейного программирования
- •2.4.1. Канонический вид злп
- •2.4.2. Симплекс-таблица, соответствующая каноническому виду
- •2.4.3. Нахождение координат вершины допустимого многогранника по каноническому виду (симплекс-таблице)
- •2.4.4. Алгоритм решения злп с помощью симплекс-метода
- •Задание для самостоятельной работы
- •2.5. Приведение злп к каноническому виду
- •2.5.1. Метод искусственного базиса
- •2.6. Алгоритм двойственного симплекс-метода
- •Задания для самостоятельной работы
- •2.7. Целочисленное линейное программирование
- •2.7.1. Метод сечения Гомори
- •2.8. Транспортная задача
- •2.8.1. Постановка задачи
- •2.8.2. Математическое описание задачи
- •2.8.3. Транспортная таблица
- •2.8.4. Таблица издержек
- •2.8.5. Метод «северо-западного» угла
- •2.8.6. Алгоритм решения транспортной задачи
- •Задания для самостоятельной работы
- •3. Нелинейное программирование
- •3.1.2.2 Метод ненаправленного поиска
- •3.1.2.3. Метод дихотомии (деление отрезка пополам)
- •3.1.2.4. Метод «золотого сечения»
- •3.1.2.5. Метод Фибоначчи
- •Задание для самостоятельного решения
- •3.2. Графический метод решения задач нелинейного программирования
- •Целевая функция линейная, ограничения нелинейны
- •Ограничения линейные, целевая функция нелинейна
- •3.3. Задачи дробно-линейного программирования
- •Задания для самостоятельного решения
- •3.4. Методы поиска безусловного экстремума функции многих переменных
- •3.4.1. Аналитический метод
- •3.4.2. Итерационные методы
- •3.4.2.1. Метод покоординатного спуска
- •3.4.2.2. Метод наискорейшего спуска
- •Задания для самостоятельной работы
- •3.5. Решение задач нелинейного программирования с ограничениями-равенствами
- •Метод неопределенных множителей Лагранжа
- •Задание для самостоятельной работы
- •3.6. Задачи квадратичного программирования
- •Задания для самостоятельной работы
- •3.7. Метод условного градиента
- •5. X1, x2,xn 0. (3.25)
- •X1, x2,xn 0.
- •Задания для самостоятельной работы
- •3.8. Метод штрафных функций
- •4. Вариационное исчисление
- •4.1. Формула Эйлера-Лагранжа
- •4.2. Частные случаи формулы Эйлера
- •4.3. Обобщенная задача вариационного исчисления
- •4.4. Решение задач вариационного исчисления с ограничениями
- •4.5. Изопериметрическая задача
- •4.6. Функционалы, зависящие от производных высших порядков
- •Задание для самостоятельного решения
- •5. Оптимальное управление
- •5.1. Постановка задачи
- •5.2. Классификация задач оптимального управления
- •5.3. Принцип максимума Понтрягина
- •5.4. Задача о максимальном быстродействии
- •Задания для самостоятельного решения
- •Список литературы
- •Основы теории оптимизации в.А. Панов
4.1. Формула Эйлера-Лагранжа
Дана следующая задача:
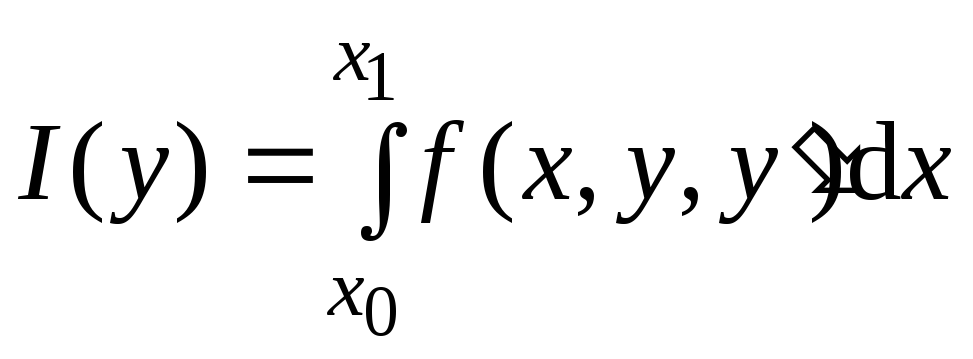 –функционал, (4.1)
–функционал, (4.1)
начальные условия: y(x0 ) = y0, y(x1 ) = y1.
Требуется найти такую функцию у(х), проходящую через точки (x0, y0) и (x1, y1), при которой данный функционал достигает максимума.
Решим задачу в общем виде.
Предположим, что функция у(х) доставляет экстремум функционалу. Зададим функции у(х) приращение у такое, что у = 0 в точках х0 и х1 и у 0 в других точках.
Найдем приращение функционала:
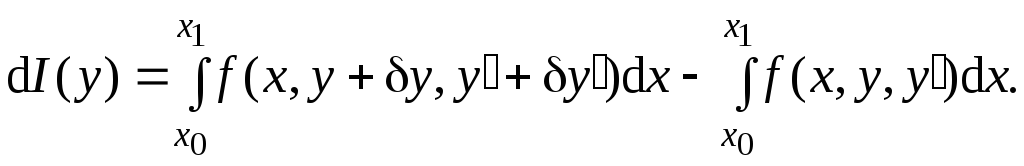 (4.2)
(4.2)
Разложим подынтегральную функцию в ряд Тейлора:
![]() (4.3)
(4.3)
где R1 – остаток. Тогда, используя (4.3):
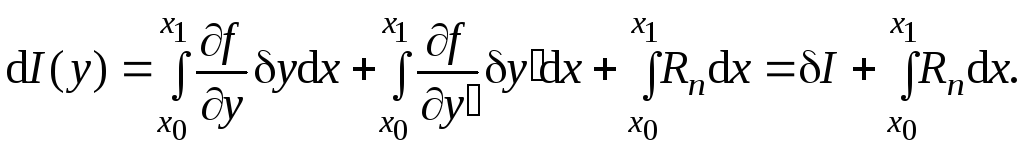
Приращение функции в точке экстремума равно нулю. По аналогии, если функция у(х) доставляет экстремум функционалу, то I = 0. I – главная часть приращения (первая вариация функционала).
I = 0, следовательно
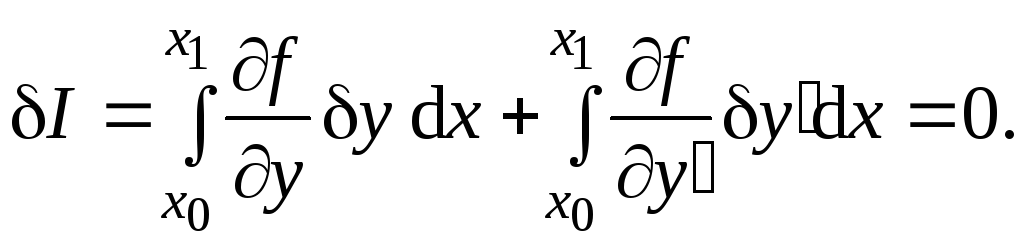 (4.4)
(4.4)
Второй интеграл уравнения (4.4) проинтегрируем по частям:
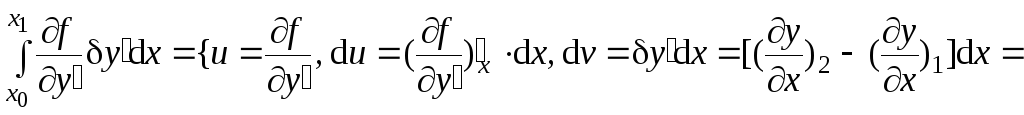
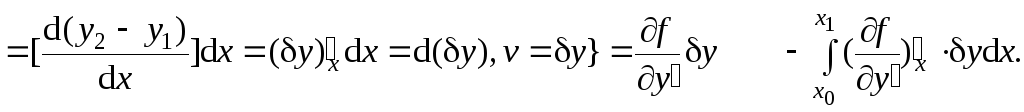

![]()
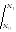 ,
так как y
в точках х1
и х0
равняется нулю. Следовательно,
,
так как y
в точках х1
и х0
равняется нулю. Следовательно,
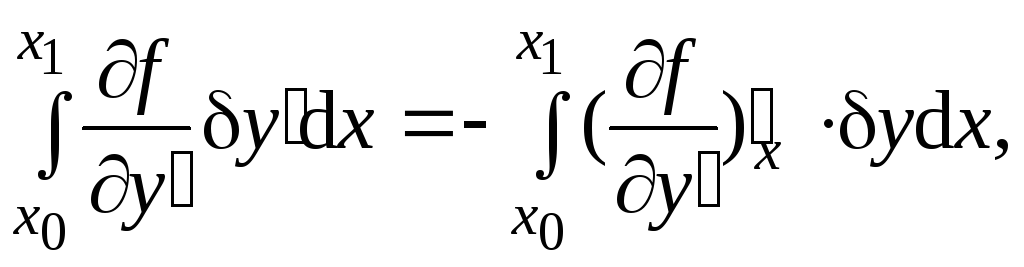 (4.5)
(4.5)
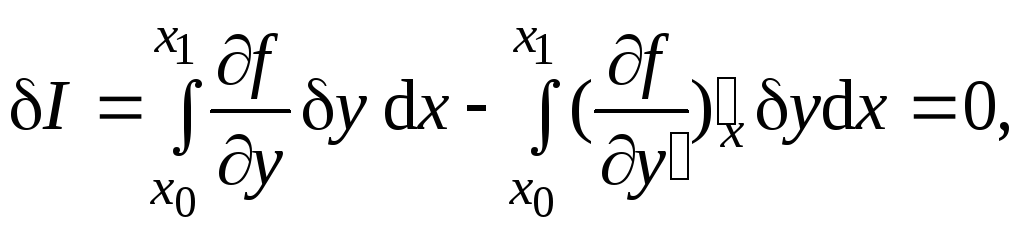 (4.6)
(4.6)
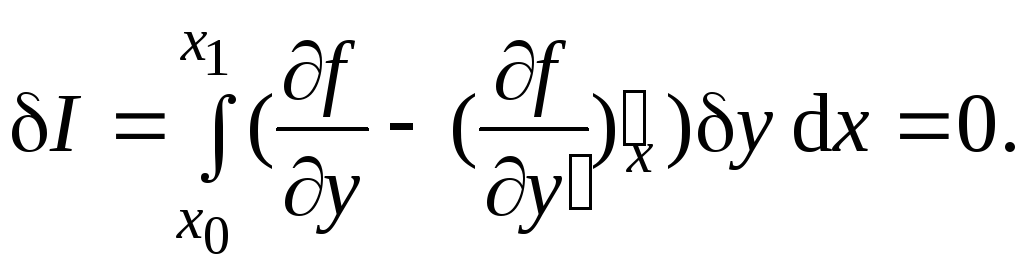 (4.7)
(4.7)
Интеграл (4.7) равен нулю, если равно нулю выражение в скобках:
![]()
или
![]() (4.8)
(4.8)
Выражение (4.8) есть формула Эйлера-Лагранжа или Эйлера.
Чтобы решить задачу вариационного исчисления, нужно решить дифференциальное уравнение Эйлера-Лагранжа (4.7) с граничными условиями: y(x0) = y0, y(x1) = y1.
Тип экстремума определяется условиями Лежандра:
fyy 0, I min, fyy 0, I max. (4.9)
Пример.
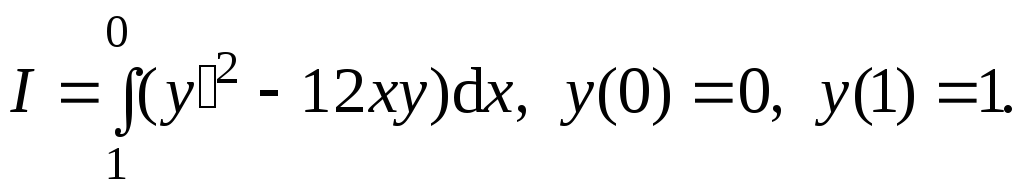
Требуется найти функцию, доставляющую экстремум функционалу и определить вид экстремума.
Решение.
1.
Запишем формулу Эйлера:
![]() ,
,
![]()
![]()
![]()
![]()
2. Решаем полученное дифференциальное уравнение:
– 12x – 2y = 0,
y = – 6x,
y = – 3x2 + c1,
y =– x3 + c1x + c2
Определяем константы: y(0) = c2 = 0
y(1) = – 1 + c1 = 1, c1 = 2,
y(x) = – x3 + 2x.
3. Определение типа экстремума: fyy = (2y)y = 2, следовательно, при найденной функции у(х) функционал достигает максимума.
4.2. Частные случаи формулы Эйлера
Рассмотрим частные случаи формулы Эйлера:
![]()
![]()
1. Подынтегральная функция f не зависит от у: f (x, y).
Формула Эйлера примет вид:
![]()
![]() (4.10)
(4.10)
Пример 1.
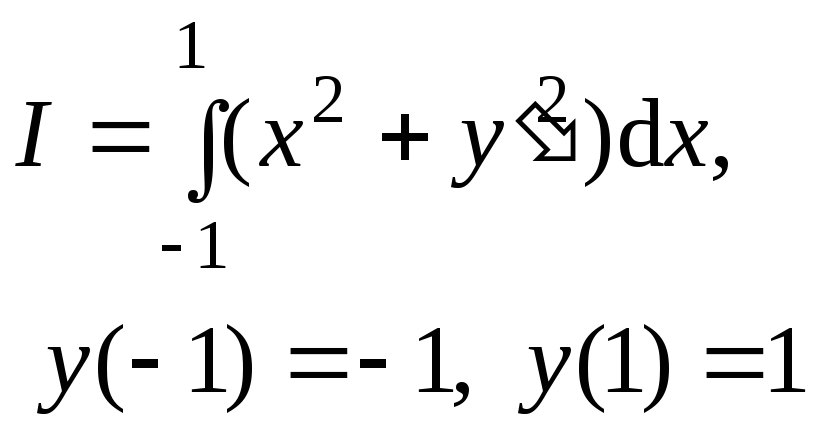
Решение.
![]()
![]()
![]()
Из начальных условий находим константы:
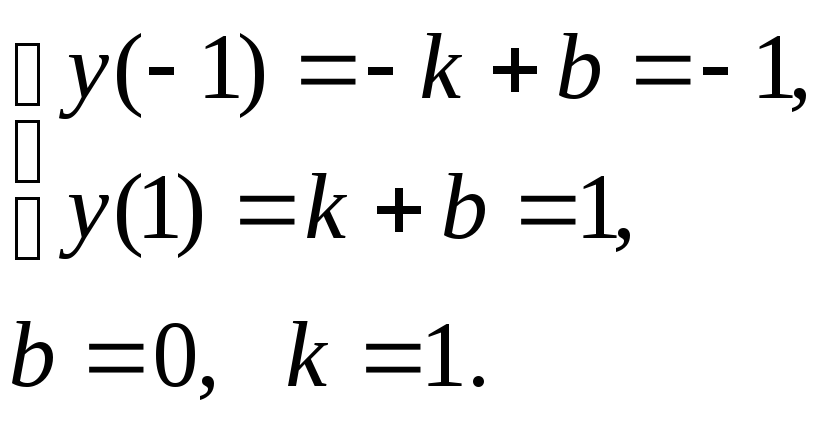
Ответ: у = х.
2. Подынтегральная функция f не зависит явно от х: f (у, y).
Найдем производную по х от выражения (f – y fy):
![]() (f
– y
fy)
= y
fy
+ y
fy
– y
fy
– y
(fy)x
= y
(fy
–
(f
– y
fy)
= y
fy
+ y
fy
– y
fy
– y
(fy)x
= y
(fy
–![]() fy).
fy).
Здесь
y
(fy
–![]() fy)
– формула Эйлера. Тогда
fy)
– формула Эйлера. Тогда
![]() (f
– y
fy
).
(f
– y
fy
).
Т.к. производная от выражения равна нулю, то выражение равно константе, отсюда
f – y fy = C. (4.11)
Пример 2. (См. задачу о кривой на плоскости, по которой скатывается шар).
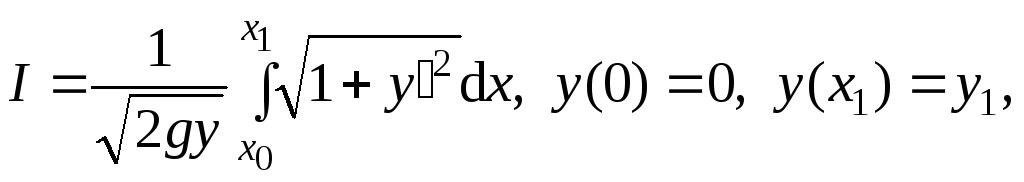
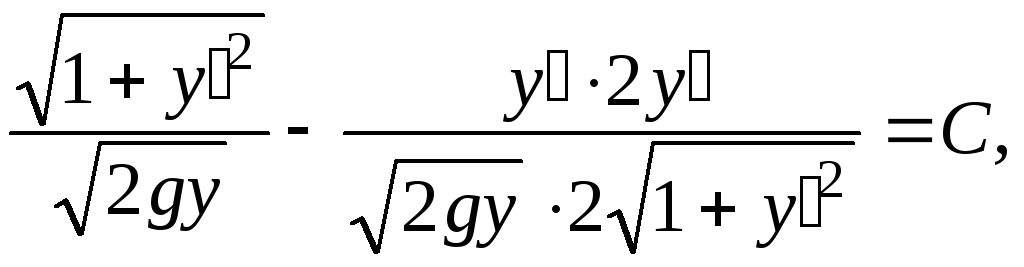
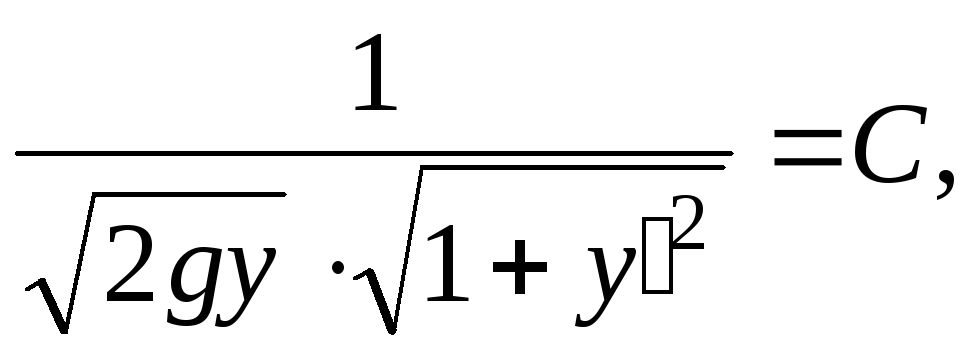

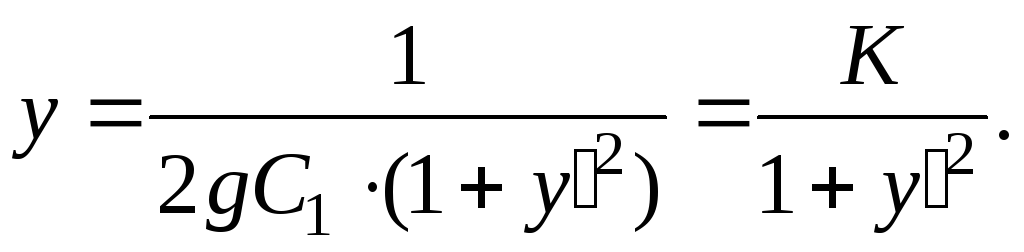
Будем
искать решение этого дифференциального
уравнения в параметрической форме:
х(t),
y(t).
Воспользуемся следующей подстановкой:
![]() .
.
Из тригонометрии:
![]()
![]()
Применим подстановку:
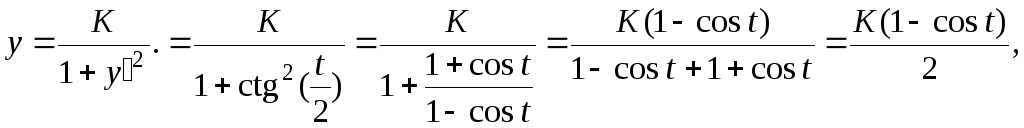
![]()
Найдем зависимость x(t). Продифференцируем полученное выражение для y(t) по х:
![]() {производная
от сложной функции}.
{производная
от сложной функции}.
![]()
![]()
Но
согласно примененной подстановке
![]()
Таким
образом,
![]()
![]()
Проинтегрируем полученное уравнение:
![]()
Решением задачи является уравнение циклоиды:

Рис. 4.1. Циклоида
4.3. Обобщенная задача вариационного исчисления
В обобщенной задаче подынтегральная функция зависит от п функций и их производных по х:
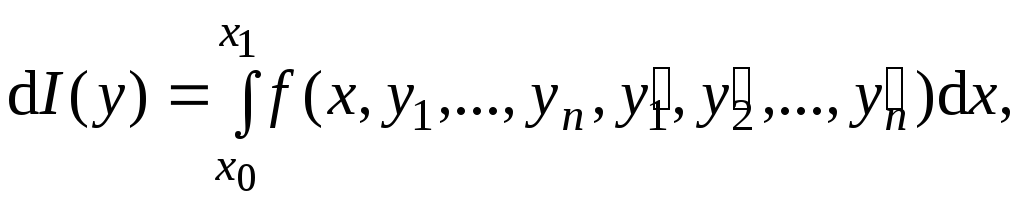
 (4.12)
(4.12)
граничные условия: yi(x0 ) = yi0, yi(x1) = yi1, i = 1,n.
Решение задачи является решением системы дифференциальных уравнений Эйлера:
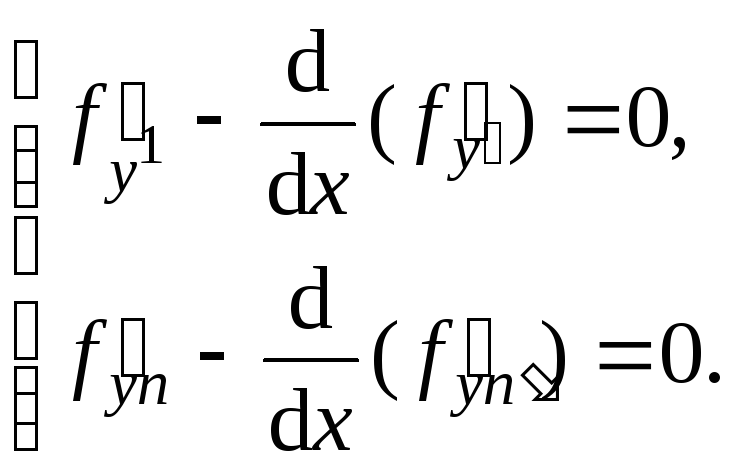 (4.13)
(4.13)
с граничными условиями:yi(x0
) = yi0,
yi(x1)
= yi1,
i
= 1,n.
граничными условиями:yi(x0
) = yi0,
yi(x1)
= yi1,
i
= 1,n.
Пример.
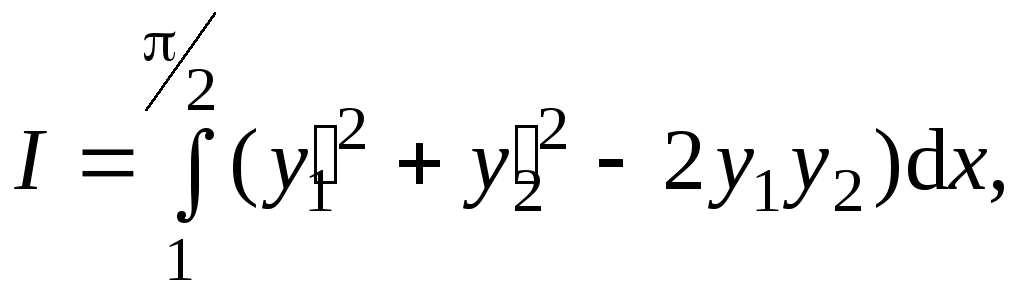
![]()
Найти функции y1 и y2, при которых функционал достигает экстремума и выполняются граничные условия.
Решение.
Составим систему уравнений Эйлера:
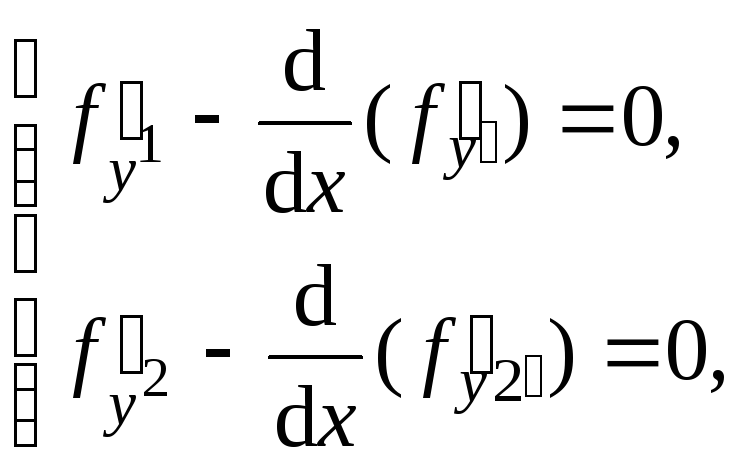
![]()
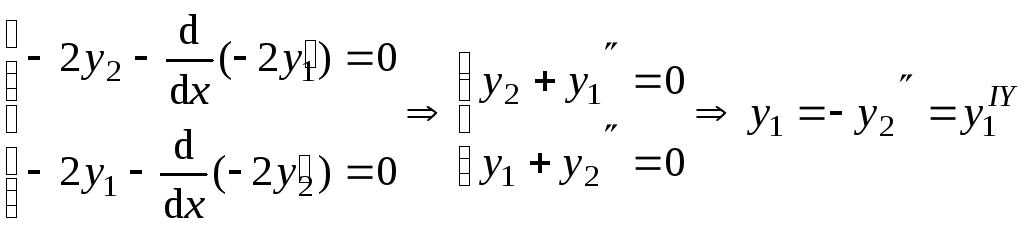
![]()
составим
характеристическое уравнение:
![]()
![]()
![]()
для
![]()
![]()
для
![]()
![]()
![]()
![]()
![]()
![]()
C1, C2, C3, C4 находятся из граничных условий.
