3. Нелинейное программирование

Признаки задач нелинейного программирования:

1. Нелинейная целевая функция.

2. Нелинейные ограничения.

Если в задаче присутствует хотя бы один признак, то она относится к задачам нелинейного программирования.

3.1. Методы поиска безусловного экстремума функции одной переменной

В задачах на поиск безусловного экстремума отсутствуют ограничения.

3.1.1. Аналитический метод

Постановка задачи: f(x) – функция одной переменной, требуется найти точки экстремума и определить вид экстремума.

1. Находится производная заданной функции и приравнивается нулю:

.

2. Находятся корни полученного уравнения х_i, ,n – порядок уравнения.

3. Определение типа экстремума по второй производной:

если , то функция в точкеимеет максимум;

если , то функция в точкеимеет минимум.

Пример.

, ,, тип экстремума – минимум.

3.1.2. Численные методы

В этих методах не требуется находить аналитическое значение производной.

3.1.2.1. Основные понятия и определения

Унимодальная функция – это функция, имеющая один экстремум, причем слева и справа от экстремума либо строго убывающая, либо строго возрастающая.

Интервал неопределенности. Отрезок а,b называется интервалом неопределенности, если внутри него функция имеет экстремум.

Точность нахождения экстремума.

Положим х₀ – точное значение экстремума, – приближенное. Тогда экстремум найден с точностью ε, если выполняется условие

Постановка задачи поиска экстремума численными методами

Дано:

1. Начальный интервал неопределенности а₀, b₀.

2. Функция f(x), унимодальная на отрезке а₀, b₀.

3. Точность нахождения экстремума ().

Требуется с заданной точностью  на отрезке а₀, b₀ найти экстремум функции f(x).

3.1.2.2 Метод ненаправленного поиска

1. Отрезок а₀, b₀ делится на N частей, где .

2. Находятся координаты точек х_i, расположенных внутри интервала неопределенности:

х_i = а₀ + (i – 1) ,

3. Рассчитываются значения функции в точках f(х_i).

4. Из полученных значений выбирается минимальное (максимальное):

F₀ = min {f(x_i)}, i = 1, (N+1),

Точка х_i, соответствующая F₀ – точка экстремума.

Достоинство алгоритма – простота, недостаток – низкая производительность (для  = 1% требуется рассчитать значения функции в 101 точке).

3.1.2.3. Метод дихотомии (деление отрезка пополам)

1. Интервал неопределенности делится пополам.

2. Находятся значения функции в двух точках, отстоящих от центра на .

3. По результату сравнения этих значений отбрасывается та часть интервала неопределенности, в которой экстремума быть не может. При этом интервал неопределенности сокращается приблизительно на половину.

4. На следующем интервале повторяются те же действия.

Рассмотрим более подробно этот метод. Пусть требуется найти минимум функции f(x) на интервале а₀, b₀ (рис. 3.1).

Рис. 3.1. Метод дихотомии

1. Находим координату центра интервала неопределенности:

.

2. Находим точки, равноотстоящие от х₀ на :

,

.

3. Находим значения функции в точках х₀ и х₀, f(х₀) и f(х₀). Пусть f(х₀) > f(х₀).

4. Отбрасываем часть отрезка левее х₀, так как там минимума нет.

Выводы по методу.

1. На каждом шаге приближения к экстремуму функция вычисляется дважды.

2. На начальных шагах интервал неопределенности уменьшается примерно на половину. По мере приближения к экстремуму, когда значение  становится соизмеримым с интервалом неопределенности, уменьшается доля отбрасываемой части, т.е. отбрасываемая часть интервала неопределенности не постоянна, что является недостатком метода.

3. Достоинство метода – производительность выше, чем в методе ненаправленного поиска. (Для нахождения экстремума с  = 1% требуется 20 вычислений функции.)

Пример 1.

Найти максимум унимодальной функции:

, .

1. 

2. , ,

, .

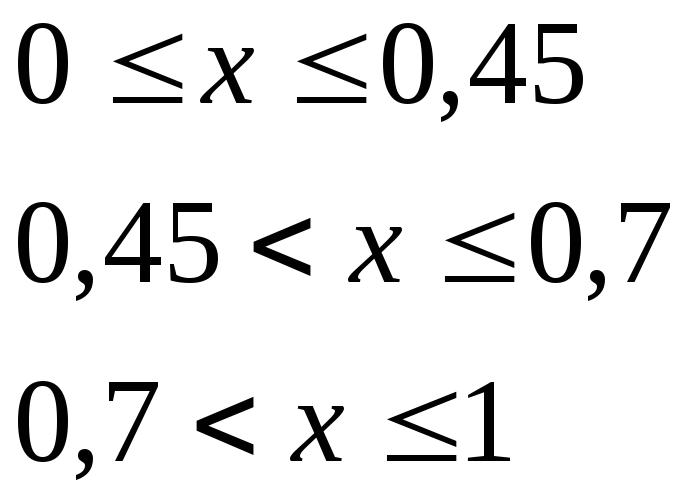
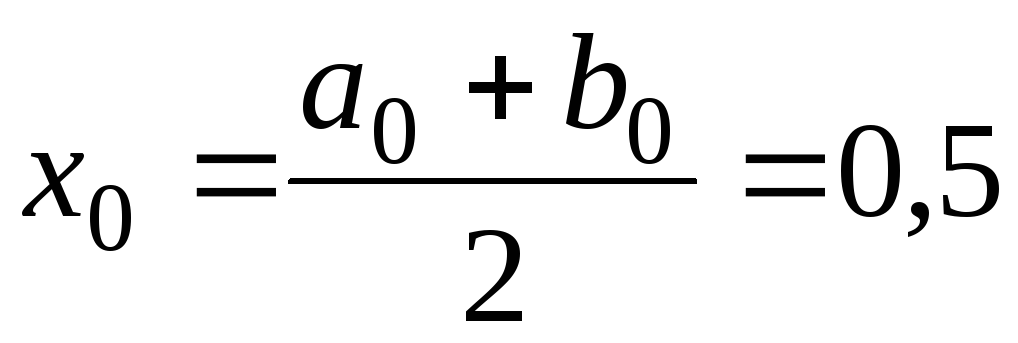
3. ,

4. ,

, следовательно, делаем еще шаг.

Пример 2.

Найти минимум функции, , ,

Решение.

1.

,

,

2.

_3.

4. И т.д.