4. Вариационное исчисление 91
4.1. Формула Эйлера-Лагранжа 91
4.2. Частные случаи формулы Эйлера 93
4.3. Обобщенная задача вариационного исчисления 96
4.4. Решение задач вариационного исчисления с ограничениями 97
4.5. Изопериметрическая задача 100
4.6. Функционалы, зависящие от производных высших порядков 103
5. Оптимальное управление 109
5.1. Постановка задачи 109
5.2. Классификация задач оптимального управления 110
5.3. Принцип максимума Понтрягина 111
5.4. Задача о максимальном быстродействии 114
СПИСОК ЛИТЕРАТУРЫ 123
Введение
Под оптимизацией в общем смысле слова понимается процесс нахождения наилучших решений с учетом имеющихся ограничений, т.е. выбора наилучшего варианта из множества имеющихся. Математические методы оптимизации начали развиваться еще до изобретения ЭВМ, однако в ту пору они применялись на практике только в самых простых случаях. Широкий переход к машинным методам выработки управленческих и проектно-конструкторских решений вызвал бурное развитие теории оптимизации и обеспечил ее широкое практическое использование.
Методы оптимизации нашли широкое применение в проектировании радиоэлектронной аппаратуры. Оптимизация в этой области состоит в определении такой совокупности внутренних параметров схемы (емкостей, сопротивлений, параметров активных элементов), при которой заранее выбранные выходные параметры схемы (например, быстродействие, потребляемая мощность) принимают наилучшие возможные значения. Помимо этого оптимизация позволяет решить ряд попутных задач: определить внутренние параметры, обладающие наибольшими коэффициентами влияния на выходные характеристики, оценить влияние дестабилизирующих факторов, обнаружить невозможность функционирования схемы или получения заданных значений выходных параметров на основе используемой структуры схемы и элементной базы. С помощью оптимизации решаются также задачи статистического характера по увеличению вероятности безотказной работы схем или числа работоспособных схем при их производстве.
Следовательно, современный инженер, в том числе и специалист по проектированию радиоэлектронной аппаратуры, не может обойтись без знания методов оптимизации. Изучению основных методов оптимизации, использующихся при проектировании технических систем, и посвящено данное учебное пособие.
1. Основные понятия и определения
В этом разделе даны определения основных понятий теории оптимизации.
1.1. Оптимизационная задача
Рассмотрим следующую задачу:
Имеется плата, на которой размещены 2 микросхемы и 2 разъема. Первая микросхема имеет 16 выводов, вторая – 24. У первого разъема 12 контактов, у второго – 36. Дано среднее расстояние от каждой микросхемы до каждого разъема. Требуется определить количество связей каждой микросхемы с каждым разъемом при условии, чтобы длина связей была минимальной.
Составим математическое описание задачи.
Введем следующие обозначения:
x1 – количество связей первой микросхемы с первым разъемом;
x2 – количество связей первой микросхемы со вторым разъемом;
x3 – количество связей второй микросхемы с первым разъемом;
x4 – количество связей второй микросхемы со вторым разъемом;
l1 – среднее расстояние от первой микросхемы до первого разъема;
l2 – среднее расстояние от первой микросхемы до второго разъема;
l3 – среднее расстояние от второй микросхемы до первого разъема;
l4 – среднее расстояние от второй микросхемы до второго разъема.
Тогда формула, выражающая среднюю длину связей:
(1.1)
Необходимо выполнить условие Q min, при этом
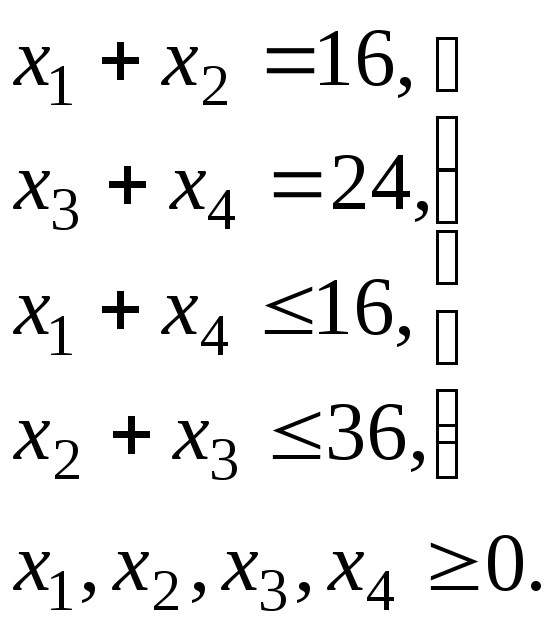(1.2)
Здесь:
(1.1) – целевая функция (ЦФ, критерий оптимальности) – математическое выражение, характеризующее качество объекта;
(1.2) – ограничения – математические выражения, связывающие переменные объекта.
Таким образом, математическое описание оптимизационной задачи представляет собой целевую функцию с ограничениями.
Формулировка оптимизационной задачи:
Найти такие значения параметров объекта, при которых целевая функция достигает минимального или максимального значения и выполняются ограничения.
Целевая функция может быть только одна. Если параметров, по которым производится оптимизация, много, то их сводят в одну функцию.