2.7.1. Метод сечения Гомори

Сущность метода:

1. Решается задача линейного программирования без требования целочисленности. Получаем решение

, .

2. Проверка полученного решения на целочисленность.

Если x_i^ – целые числа, то задача решена, если нет – выполняются следующие действия:

• От допустимого многогранника отсекается часть площади. Точка с координатами x_i^ должна попасть в отсекаемую область (рис. 2.4). Математически это отсечение обозначает введение дополнительного ограничения.

• Решается задача с количеством ограничений, увеличенным на единицу.

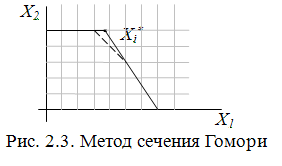
Рис. 2.4. Метод сечения Гомори

Получение дополнительного ограничения

Введем следующие обозначения:

Х – целая часть Х, Х  Х .

Например, 4,2 = 4, –4,2 = –5.

Х – дробная часть Х, Х = Х – Х, Х 0.

Предположим, имеется задача линейного программирования, приведенная к каноническому виду (2.15):

(2.15)

Выразим базисные переменные через свободные:

(2.16)

В этом выражении х_i должны быть целыми. Преобразуем (2.16):

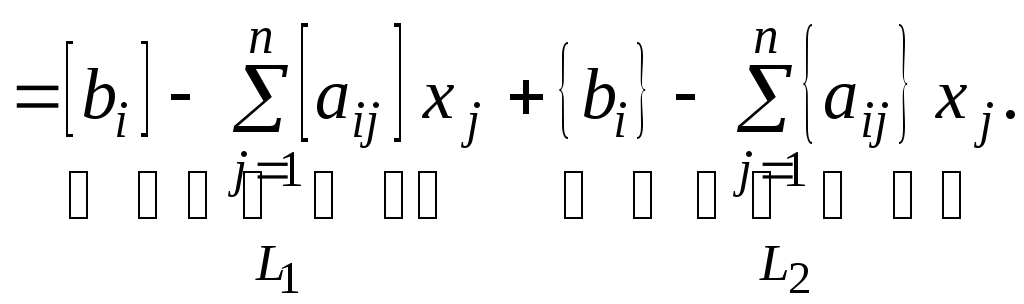(2.17)

Если x_n+i – целочисленные, то L₁ – всегда целочисленное, L₂ – в общем случае может быть не целочисленным, но для данной задачи L₂ должно принимать следующие значения: 0, –1, –2,, т.е.

L₂  0, (2.18)

(2.19)

Преобразуем ограничения-неравенства (2.19) в ограничения-равенства:

(2.20)

Последнее ограничение и является искомым дополнительным ограничением. В качестве l-ой берется та строка симплекс-таблицы, которая имеет максимальную дробную часть коэффициента b_i.

Алгоритм метода сечения Гомори

1. Задача линейного программирования приводится к каноническому виду и составляется симплекс-таблица.

2. Решается задача симплекс-методом без учета целочисленности.

3. Окончание решения в случае целочисленности.

4. Если решение не целочисленно, то в таблицу вводится строка, имеющая коэффициенты –a_ij, –b_i той строки таблицы, которая имеет максимальную дробную часть коэффициента правой части ограничений.

5. Решается задача линейного программирования двойственным симплекс-методом.

Пример 1.

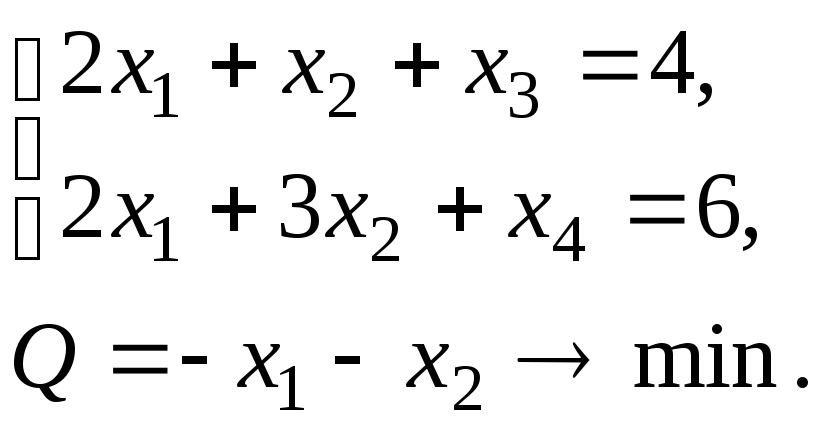
1. Задача уже приведена к каноническому виду. Составляем симплекс-таблицу и решаем задачу симплекс-методом:

	1	2
3	2	1	4
4	2	3	6
	–1	–1	0

	3	2
1	1/2	1/2	2
4	–1	2	2
	1/2	–1/2	2

	3	4
1	3/4	–1/4	3/2
2	–1/2	1/2	1
	1/4	1/4	5/2

Получено оптимальное решение, но это решение не целочисленно.

2. Вводим дополнительную строку.

Первое ограничение имеет максимальную дробную часть коэффициента b, следовательно, коэффициентами нового ограничения будут являться дробные части элементов первой строки симплекс-таблицы, взятые с обратным знаком.

3/4 = 1/4, –1/4 = 3/4, 3/2 = 1/2:

	3	4
1	3/4	–1/4	3/2
2	–1/2	1/2	1
5	–1/4	–3/4	–1/2
	1/4	1/4	5/2

3. Далее решаем задачу двойственным симплекс-методом.

	3	5
1	1	–1/3	5/3
2	–1	2/3	2/3
4	1	–4/3	2/3
	0	1/3	7/3

4. Снова получено нецелочисленное решение. Вводим новое ограничение. При равенстве дробных частей выбирается любая строка (в данном примере рассмотрена последняя строка)

1 = 0, –4/3 = 2/3, 2/3 = 2/3

	3	5
1	1	–1/3	5/3
2	–1	2/3	2/3
4	1	–4/3	2/3
6	0	–2/3	–2/3
	0	1/3	7/3

Решаем полученную таблицу двойственным симплекс-методом:

	3	6
1	1	–1/2	2
2	–1	1	0
4	1	–2	2
5	0	–3/2	1
	0	1/2	2

Все переменные целочисленные, следовательно, получено искомое решение:

x₁ = 2, x₂ = 0, x₃ = 0, x₄ = 2, Q_min = –2.

Пример 2.

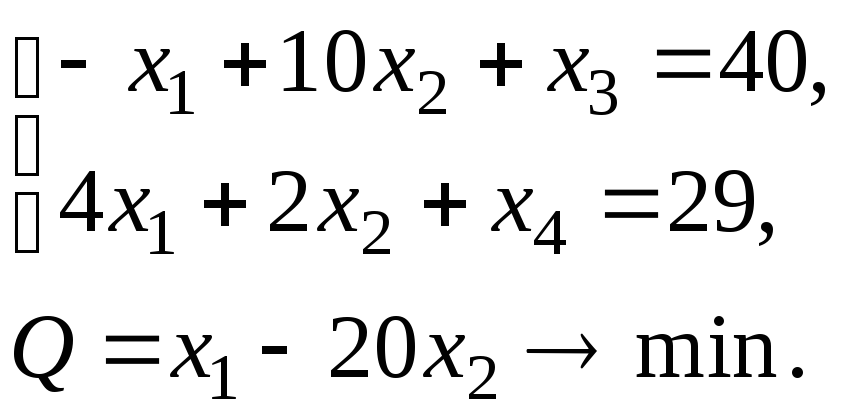
Решение

1. Задача уже приведена к каноническому виду. Составляется симплекс-таблица и решается задача симплекс-методом:

	1	2
3	–1	10	40
4	4	2	29
	1	–20	0

	1	3
2	–1/10	1/10	4
4	42/10	–2/10	21
	–1	2	80

	4	3
2	1/42	4/42	9/2
1	10/42	–2/42	5
	10/42	82/42	85

Получено оптимальное решение, но это решение не целочисленно.

2. Вводится дополнительная строка:

	4	3
2	1/42	4/42	9/2
1	10/42	–2/42	5
5	–1/42	–4/42	–1/2
	10/42	82/42	85

Для перехода к допустимому базисному решению находится разрешающий элемент и преобразуется симплекс-таблица:

	5	3
2	1	0	4
1	10	–1	0
4	–42	4	21
	10	1	80

Все переменные целочисленные, следовательно, получено искомое решение:

x₁ = 0, x₂ = 4, x₃ = 0, x₄ = 21, Q_min = –80.