8.1.Плоские графики

8.1.1.Команда plot

Команда plot создает x-y график в линейных осях; если x и y являются векторами одинаковой длины, то команда plot(x,y) открывает графическое окно и рисует зависимость y(x). Вы можете нарисовать график синуса на интервале от -4 до 4 с помощью команды

x = -4:.01:4; y = sin(x); plot(x,y)

Попробуйте это сделать сами. Вектор x является набором равноотстоящих точек с шагом 0.01, а y - вектор со значениями функции синуса в этих точках (вспомните, что синус - поэлементная функция). Рисунок при создании открывает отдельное окно. Переход между окнами (возврат в окно MATLAB или переход от рисунка к рисунку осуществляется в соответствии с правилами среды, например, с помощью комбинации Alt+Tab или с помощью мыши). В качестве второго примера вы можете нарисовать график e−x2 на интервале от -1.5 до 1.5 следующим образом: x = - 1.5:.01:1.5; y = exp(-x.ˆ2); plot(x,y). Обратите внимание на то, что точка перед ˆ обязательна, поскольку мы хотим, чтобы возведение в степень выполнялось поэлементно (см. п. 3.3 ). Можно, например, рисовать кривые, заданные параметрически. Попробуйте, например, выполнить такой оператор t=0:.001:2*pi; x=cos(3*t); y=sin(2*t); plot(x,y).

Аргументами функции plot могут быть различные комбинации векторов и матриц. Возможны следующие варианты:

•plot(y)

–Если y - вектор, то будет нарисована кривая y как функция номера элемента в y.

–Если y - матрица, то будет сгенерирован набор кривых, каждая из которых представляет собой зависимость столбца матрицы от номера строки.

•plot(x,y)

–Если x и y - вектора одинаковой длины и размерности (оба строки или оба столбцы), то будет нарисована кривая y от x.

–Если x - вектор, а y - матрица, строки или столбцы y будут нарисованы в зависимости от x. Если столбец матрицы y имеет ту же длину, что и вектор x, то будет построен набор кривых, представляющий зависимость каждого из столбцов от x. Если строка матрицы y имеет ту же длину,

135

что и вектор x, то будет построен набор кривых, представляющий зависимость каждой из строк от x. Если число строк и столбцов y одинаково, то строятся столбцы от x.

–Если x - матрица, а y - вектор, то будет построено несколько кривых представляющих зависимость y от строк или столбцов матрицы x по правилу, описанному в предыдущем пункте.

–Если x и y - матрицы одинаковой размерности, то будет построен набор кривых, представляющих столбцы y от столбцов x.

Если у вас цветной монитор, то вы уже обратили внимание, что при описанном способе вызова функции plot различные кривые на одном и том же графике отрисовываются разным цветом. Перебор цветов выполняется автоматически, а при использовании соответствующих аргументов у команды plot эти цвета можно выбирать (см. далее).

Число аргументов у команды plot не ограничивается двумя. Можно использовать эту команду в формате plot(x1,y1,x2,y2,...), причем правила, описанные выше, относятся к каждой паре аргументов.

Иногда для отрисовки кривой используется функция line с теми же аргументами, что и функция plot. Различие станет ясно после знакомства с дескрипторной графикой низкого уровня (см. п. 8.4).

Представляет интерес познакомиться с функцией comet(x,y), которая строит движущуюся двумерную кривую с головой другого цвета. И хотя такое отображение не является анимацией в полном смысле слова, поскольку выполняется отрисовка уже насчитанных точек, тем не менее при построении сложных параметрических кривых полезно использовать эту функцию (например, в задаче исследования кривых Лиссажу).

8.1.2.Разметка графика и надписи

Команда grid поместит сетку на график. График может быть снабжен заголовком, именами осей, и на сам график может быть помещен дополнительный текст с помощью команд вывода текста. Аргументами всех этих команд является текстовая строка. Например, команда title(’График наилучшего приближения’)

добавит к вашему графику заголовок. Команда gtext(’Пятно’) позволяет с помощью мыши или клавишного курсора разместить на рисунке индикаторный крест, в месте размещения которого и будет помещен текст после нажатия произвольной клавиши. При необходимости сделать подписи осей используются команды

Xlabel(’ПодписьX’), Ylabel(’ПодписьY’). При необходимости вывести в каче-

136

стве надписи какую-либо комбинацию символов, которые отсутствуют в стандартном текстовом процессоре (например, верхние и нижние индексы, формулы и т.д.), вы можете использовать стандартную нотацию LaTeXа (подробнее о LaTeX вы можете узнать, например в [10]). Если выведена неправильная надпись, то можно ее стереть или заменить на другую, повторив такую же команду вывода текста, но с пустой или новой строкой в качестве аргумента.

Для изображения нескольких кривых на одном рисунке существуют два способа, которые иллюстрируются следующими примерами.

1.x=0:.01:2*pi;

y1=sin(x);

y2=sin(2*x);

y3=sin(4*x);

plot(x,y1,x,y2,x,y3)

или, что полностью эквивалентно, формируется матрица Y, содержащая значения изображаемых функций в виде столбцов, и после этого рисунок создается последовательностью команд

x=0:.01:2*pi;

Y=[sin(x)’, sin(2*x)’, sin(4*x)’]; plot(x,Y)

2.Другим способом такого рисования является использование команды hold on, которая замораживает текущий график, так что последующие кривые помещаются на этот же график. При этом масштаб и разметка осей изменяются, если новая кривая не вписывается в нарисованные оси. Команда hold off приводит к тому, что любой последующий вызов команды plot создает новый рисунок на этом же листе, т.е. предыдущий график стирается.

При выводе графика можно сменить принятый по умолчанию тип точек, с помощью которых рисуется данный график. Например, последовательность команд

x=0:.01:2*pi;

y1=sin(x);

y2=sin(2*x);

y3=sin(4*x); plot(x,y1,’--’,x,y2,’:’,x,y3,’+’)

приведет к тому, что первый график будет нарисован пунктиром, второй – точками, а третий – символами + (рис. 4). В общем случае каждая линия на графике определяется триплетом x,y,s, где x и y - это вектора с координатами, а s - строковая

137

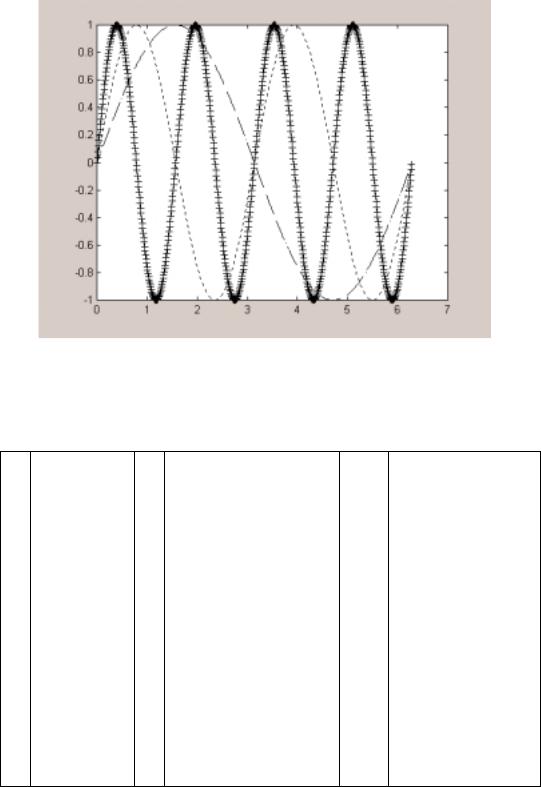
Рис. 4. Пример графика Sin(x), Sin(2x) и Sin(3x)

переменная, образованная любыми комбинациями из каких-нибудь приведенных ниже столбцов.

hвосьмиугольник

8.1.3.Управление осями при выводе графиков

По умолчанию масштаб осей выбирается автоматически так чтобы график целиком поместился в окне, причем с разумным запасом. Кроме того, оси автоматически

138

размечаются и по умолчанию выбирается декартова система координат с началом координат 5, в левом нижнем углу. Эта автоматическая установка может быть изменена с помощью команды axis. Использование этой функции применительно к плоским графикам описано в следующей далее таблице.

5 Началом координат считается точка с координатами xmin, ymin.

139