63. Вариациялық есептеу. Әлді минимум. Әлсіз минимум. Қарапайым есеп.
ВАРИАЦИЯЛЫҚ ҚИСАП
Алдыңғы
дәрістерде
-де
берілген U
жиынында
функциясының
ең кіші мәнін анықтаудың негізгі
теориялары мен сандық әдістерін
баяндағанбыз. Мұндағы
-
n
векторлар
кеңістігі
еді. Енді
орнына
кесіндісінде үзіліссіз дифференциалданатын
функцияларының кеңістігін алып, оны
арқылы белгілейік.
жиыны
ретінде
кеңісгінде қандай да бір жиынды аламыз.
Әрбір
элементіне
Ε1-ден
қандай да бір санды сәйкестендіру үшін
орнына
келесі анықталған интегралды қарастыру
қажет.
.
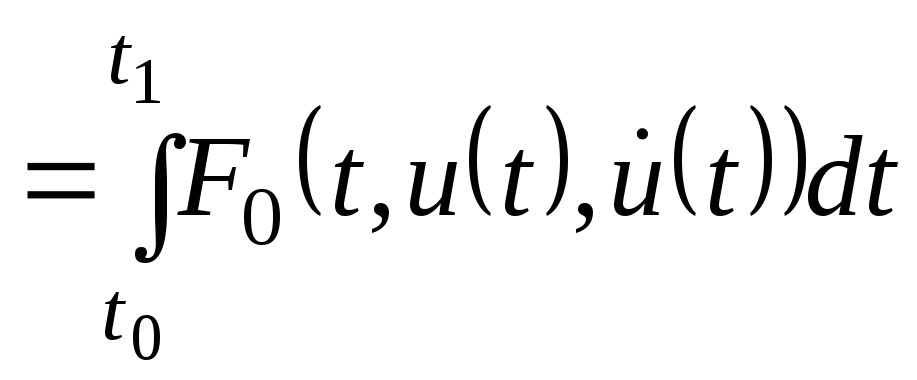Нәтижесінде қайтадан тиімділік есебін аламыз:
Вариациялық қисап осындай тиімділік есебін шешу теориясының негіздерін зерттейді.
Брахистохрон есебі. 1696 жылы И.Бернулли әлем математиктеріне мынадай есеп қойыпты: Тік жазықтықта әр түрлі деңгейде орналасқан, бір түзу бойында жатпайтын екі нүкте А мен В берілген. Осы нүктелерді қандай қисықпен қосқанда сол қисық бойымен өз салмағының әсерінен қозғалатын материалдық нүкте А -дан В-ға ең қысқа уақытта жетеді?
Осы есептің шешімін тапқан И.Бернуллидің өзі, Лейбниц, Я.Бернулли және қолы қойылмаған тағы бір автор болыпты. Кейіннен қол қоймаған автор И.Ньютон екендігі анықталыпты деген сөз бар.
Аталмыш
есепке тоқталайық:
кординат басы А(0,
0)
нүктесіндегі
және x
өсі горизонтәл, ал у
өсі вертикәл төмен бағытталған
координат
жүйесін таңдап
аламыз. А
нүктесі
нүктесінен
жоғары
орналассын
делік. Мәселен
А
мен В
арқылы
өтетін
ізделінді у
= у(х)
қисығындағы
нүкте болсын. Үйкеліс жоқ деп
есептесек
кинетикалық энергия Т
мен потенциалық энергия П
қосындысы
қисығының
кез келген нүктесінде
тұрақты. А
нүктесінде дене тыныштықта
тұрады, ендеше
,
ал М
нүктесінде
.
Осыдан М
нүктесіндегі
жылдамдықты анықтаймыз
Лездік жылдамдық
онда
.
Демек
Осыдан
(1)
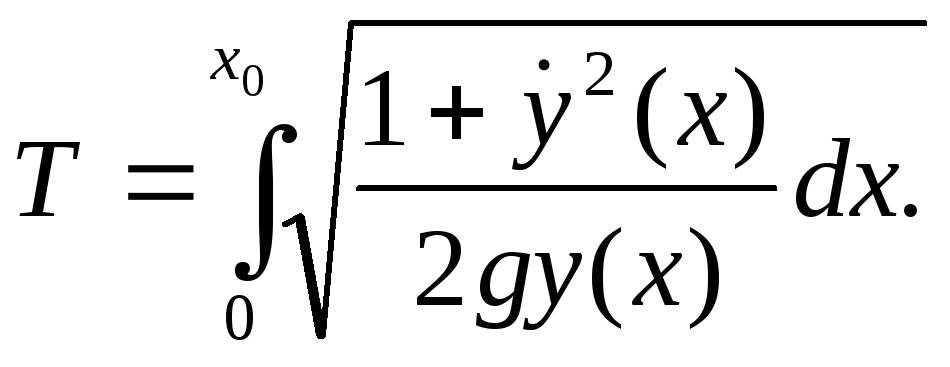
Бұл
(1) - формула А
мен В
нүктесі арқылы өтетін кез келген
,
қисығы
бойымен дененің қозғалу уақытын
білдіреді.
Байқайтынымыз:
,
,ал
есептің өзінің жазылуы:
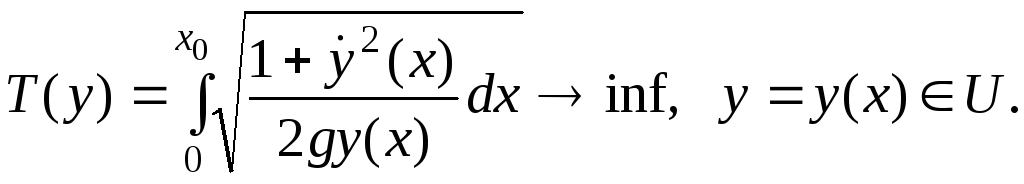(2)
Жай есеп. Жоғарыдағы (2) есебін келесі түрде жалпылайық.
(3)
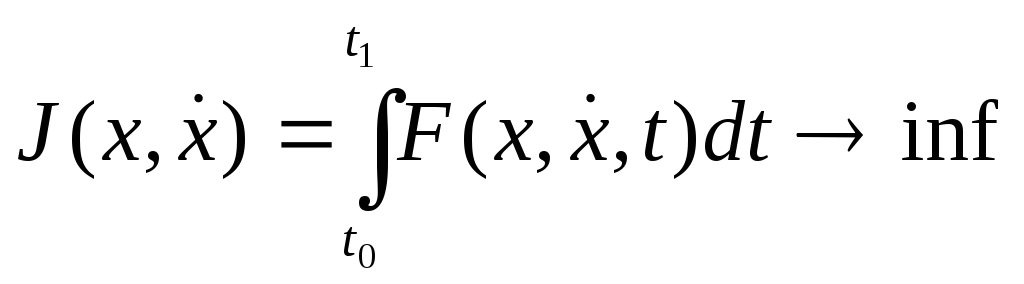
Функционалын
(4)
жиынында минимумдау керек.
Егер
х,
t
айнымалыларын
тиісінше
у,
x айнымалыларына
алмастырсақ
онда
(3) пен
(4)-тен
(2) есебі
шығатынын
көреміз.
(мұндағы
-
үзіліссіз
функция)
белгілеулерін
енгізсек
(3), (4) есебі
(5)
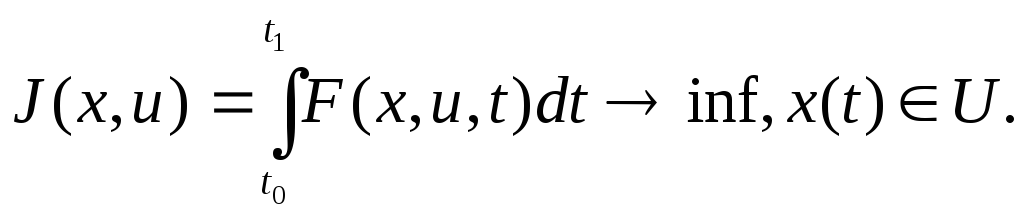
түрінде жазылады.
1-анықтама.
Егер
орындалатын
кез
келген
ұйғарымды
функциясы
үшін
теңсіздігі
(мұндағы
)
орындалатын
саны
табылса,
онда
(5) (немесе
(3), (4)) есебіндегі
функционалын
функциясы
әлді
локәлдік
минимумге
жеткізеді
дейміз.
2-анықтама. Егер
(6)
орындалатын
кез
келген
ұйғарымды
функциясы
үшін
теңсіздігі
орындалатын
ε
>
0
саны
табылса
онда
(5)-(немесе
(3), (4)) есептегі
функционалын
функциясы
әлсіз
локәлдік
минимумге
жеткізеді
дейміз.
Ескерту:
1 - анықтамадағы
функционалының
мәні
әрбір
үшін
нүктесінің
ε
аймағында
орналасқан
ұйғарымды
функциялар
жиынындағы
J(x0,
u0)
мәнімен
салыстырылады,
ал
2-анықтамада
салыстыру
әрбір
үшін
тиісінше
x(t)
және
нүктелерінің
ε
аймақтарында
орналасқан
ұйғарымды
x0(t)
және
функцияларының
жиынында
жүргізіледі.
Сондықтан
нүктесіндегі
әлсіз
локәлдік
минимум
шарты
әлді
локәлдік
микимум
шарты
болып
табылады.
Екінші
жағынан
нүктесінде
әлді
локәлдік
минимумге
жетеміз,
ендеше
бұл
нүктеде
әлсіз
локәлдік
минимум
да
жүзеге
асады,
өйткені
,
шарты,
дербес
жағдайда
болатын
үшін
де
орындалады.
Кері
тұжырым
дұрыс
емес.
Әлсіз
локәлдік
минимумның
қажетті
шарттары.
Мына
x(t)U,
тиістіліктерден
шығатыны
.
Демек
x(t)U
ұйғарымды
функциясын
түрінде
таңдаған
жөн,
мұндағы
- қай
бір
сан.
Сонымен
,
h(t)U0
болғандықтан
γ
санын
тандау
арқылы
(1), (2) анықтамалардағы
теңсіздіктерді
қамтамасыз
етуге
болады.
Мәселен
F(x,
и,
t)
функциясы
аргументтері
бойынша
екі
рет
үзіліссіз
дифференциалданатын
функция
делік.
Онда
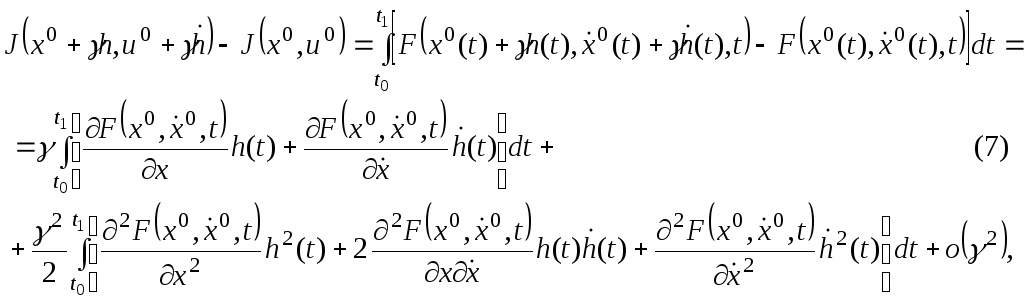мұндағы
x0
=x0(t)U.
Белгілеу
енгізейік:
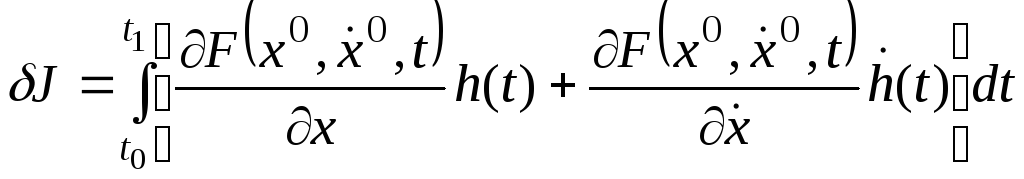(8)
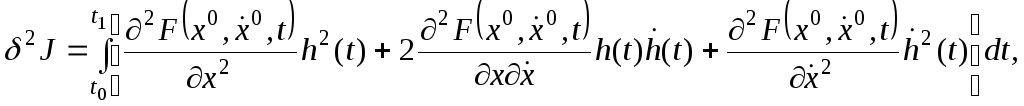(9)
Бұдан соң (7) өрнекті келесі түрде жазамыз:
(10)
Жоғарыдағы
(8) - формуламен
анықталатын
J
шамасы
функционалының
нүктесіндегі
бірінші
вариациясы
деп,
ал
(9)-дағы
2J
шамасы
функционалының
нүктесіндегі
екінші
вариациясы
деп
аталады.
1-теорема.
Мәселен
функциясы
функционалын
U
жиынында
әлсіз
локәлдік
минимумге
жеткізсін
дейік.
Онда
келесі
шарт
орындалуы
қажет
J=0, 2J0. (11)
Дәлелі.
Кейбір
γ
саны
мен
функциясы
үшін
(6) -теңсіздік
орындалсын
делік.
Мұндағы
және
.
(11) өрнектің ақиқаттығын
көрсетейік. Жоғарыдағы
(10) өрнектен
мұндағы
|
|
>
0
- жеткілікті
аз сан,
,
||
0, Осыдан,
егер
J0,
онда таңбасы J
-ге қарама қарсы
γ
санын әрқашан таңдап алуға болады.
Бұл
шақта
.
Бұл
шартына қайшы. Демек J=0.
Бұдан соң
J=0
болғандықтан
Осыдан
шығатыны:
егер 2J<0
онда жеткілікті аз ||>0
үшін
,
бұл
шартына
қайшы. Теорема дәлелденді.
J=0 шартын әлсіз локәлдік минимумның бірінші ретті қажетті шарты деп ал (11) шартын локәлдік минимумның екінпгі ретті қажетті шарты деп атаймыз. (11) - шарт сонымен қатар әлді локәлдік минимум шарты да болады.
Лагранж
леммасы.
Егер
-
үзіліссіз функция және
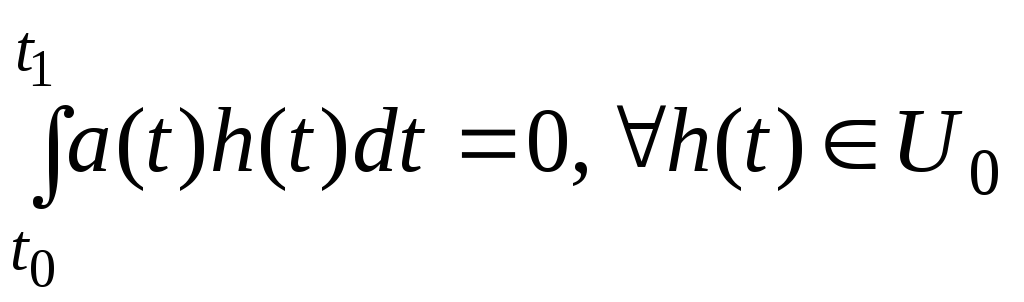(12)
онда
Дәлелі.
Қарсы жориық
яғни кейбір
нүктеде
.
Мәселен,
анықтық үшін
сан
делік. Онда
функциясының
үзіліссіздігінен
кезінде
болатын
ε0>0
саны
табылады.
функциясын
келесі түрде таңдаймыз:
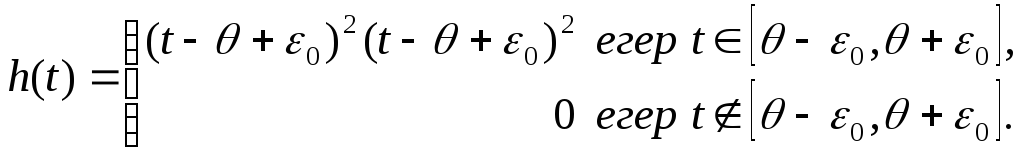
Онда интеграл
Бұл (12) шартына қайшы. Лемма дәлелденді.
Эйлер
теңдеуі.
Ізделінді
функциясы Эйлер тендеуі деп
аталатын дифференциаддық теңдеулердің
шешімі болатынын көрсетейік. Эйлер
теңдеуінің
алғашқы
қорытылуын Лагранж леммасының
негізінде аламыз.
2-теорема.
функциясы
(5)
– есептегі
J(x,
и)
функционалын
әлсіз локәлдік минимумге жеткізуі үшін
осы функция Эйлер тендеуін:
(13)
қанағаттандыруы қажет.
Дәлелі.
Жоғарыдағы (6) - теңсіздігін
қанағаттандыратын барлық
үшін
J(x,
и)
J(x0,
и0)
орындалсын дейік.
Сонда
көрсетілген функциялар
(13) тендеудің шешімі екендігін көрсетейік.
Шынында да, бірінші ретті қажеттілік
шартына сай
нүктесіндегі
бірінші вариация:
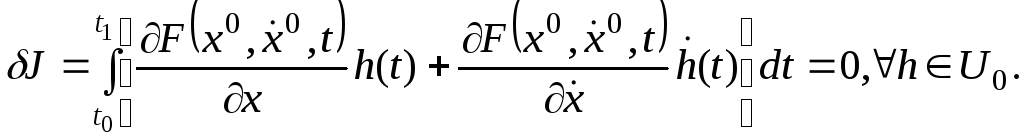(14)
Бөліктеп интегралдағаннан кейін екінші қосылғыш
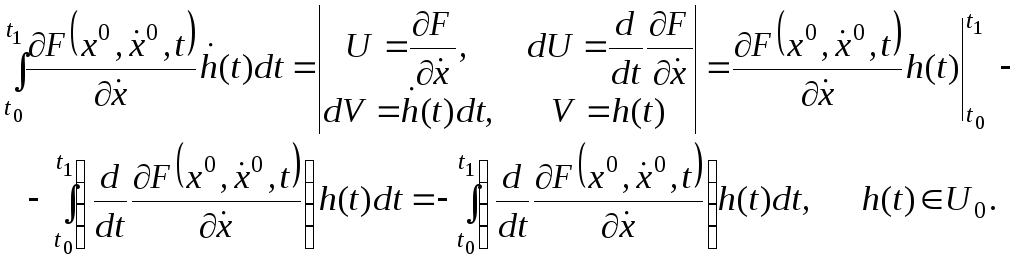
түрінде жазылады. Енді (14) өрнегін мына түрде өрнектейміз
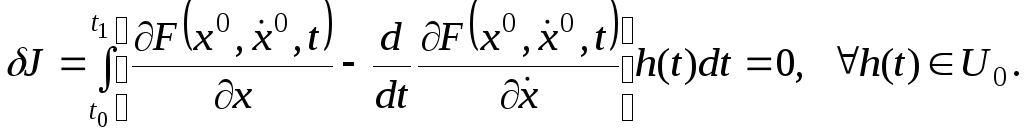
Осыдан, Лагранж леммасына орай
десек
(13) теңдеу алынады. Теорема дәлелденді.
Бойында Эйлер тендеуі орындалатын
функциялары экстремәлдар деп аталады.
ДЮБУА-РЕЙМОН ЛЕММАСЫ. БОЛЬЦ ЕСЕБІ.
ВЕЙЕРШТРАСТЫҢ ҚАЖЕТТІ ШАРТЫ
Бұл дәрісте Эйлер тендеуін Дюбуа-Реймон леммасы негізінде қорыту және Эйлер теңдеуінің анализі келтірілген. Больц есебі үшін локәлдік әлсіз минимумның қажетті шарты алынған. Жай есеп үшін әлді локәлдік минимумның қажетті шарттары анықталған.
Дюбуа-Реймон
леммасы.
Егер
үзіліссіз
болса және
,
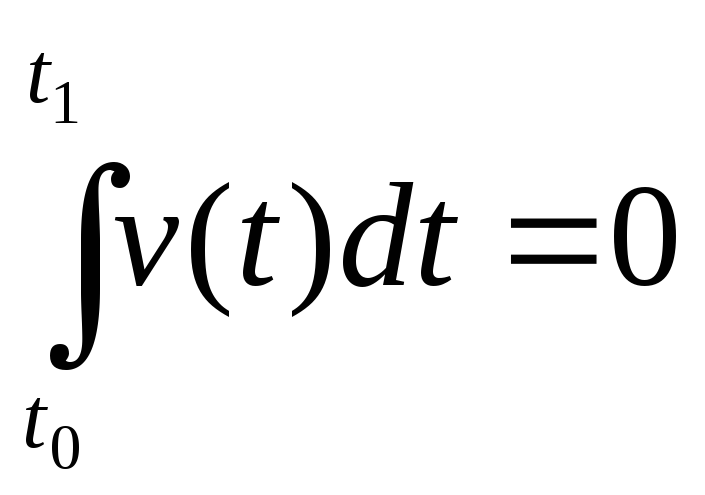(1)
шартты
қанағаттандыратын
кез келген
функциясы үшін анықталған интеграл
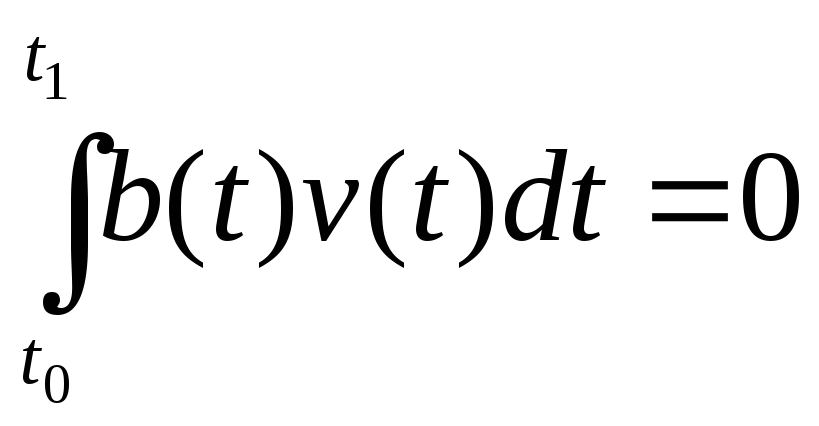(2)
болса
онда
Дәлелі.
Қарсы жориық,
яғни
болатын
кесіндісінің
және
нүктелері табылады дейік. Анықтық үшін
.
Мына
кесінділері
бір бірімен
қиылыспайтын
әрі
,
болатын
жеткілікті аз ε0
санын таңдап алайық. Функция
үзіліссіз,
онда соңғы теңсіздік орындалады.
(1) шартын қанағаттандыратын
функциясын
төмендегіше құрамыз:
Онда интеграл
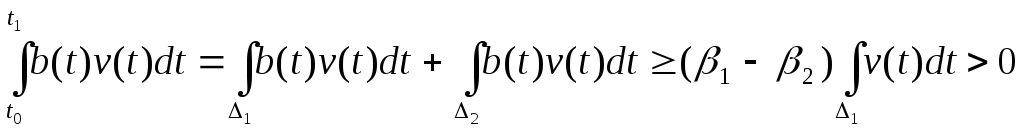
Бұл 2-тендікке қайшы. Лемма дәлелденді.
Дюбуа-Реймон леммасы негізінде Эйлер тендеуін екінші рет қорытып шығаруға болады. Шынында да, бірінші ретті қажеттілік шартынан
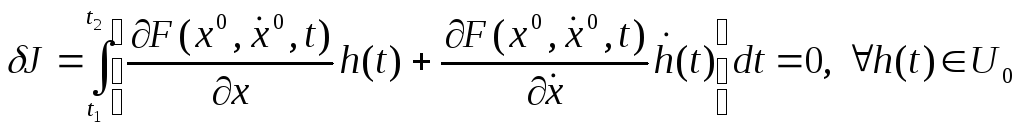
бірінші қосылғышты бөліктеп интегралдаған соң
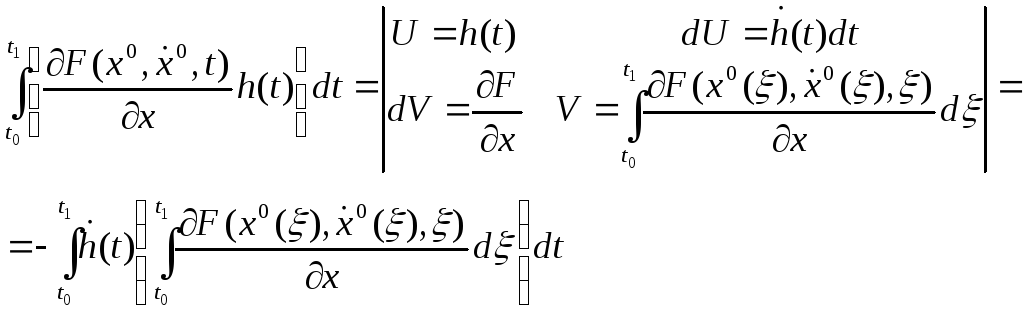
алатынымыз
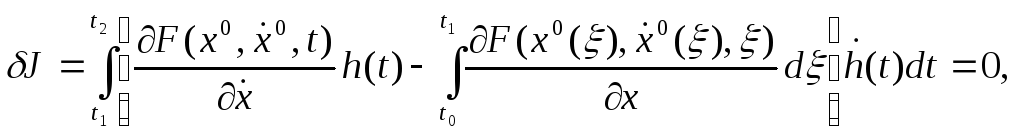
Осыдан
мыналарды ескеріп
,
яғни
және
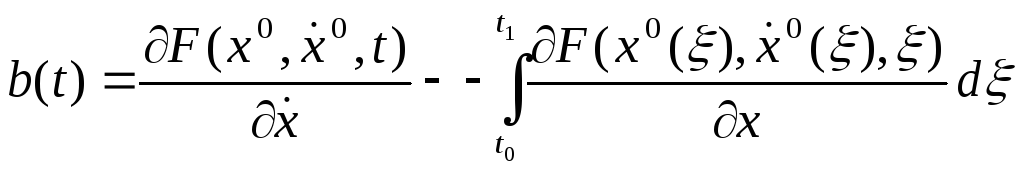
белгілеуін енгізіп, Дюбуа-Реймон леммасына орай Эйлер тендеуін Дюбуа-Реймон формасында, келесі түрде аламыз:
.
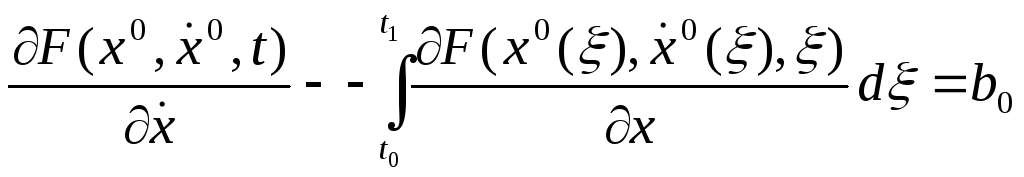(3)
|(3)-тегі екінші қосылғыш t бойынша дифференциалданады және оң жақта дифференциалданады, демек бірінші қосылғышта t бойынша дифференциалданады. Ендеше (3) - тен белгілі Эйлер теңдеуін аламыз.
. (4)
Қолданбалы есептерді шешуге қолайлылық үшін (4)-тендеу келесі түрде жазылуы мүмкін:
.
(5)
функциясы
айнымалылары
бойынша
екі рет дифференциадданатын функция.
Екінші ретті дифференциаддық тендеу
(5)
түріндегі шешімге ие, мұндағы
тұрақтылыры
шарттарынан
анықталады.
1-мысал.
Брахистохрон есебіндегі функция
.
Демек
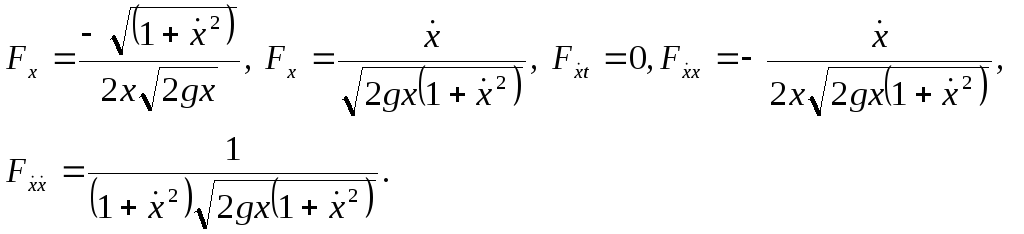
(5)-теңдеу
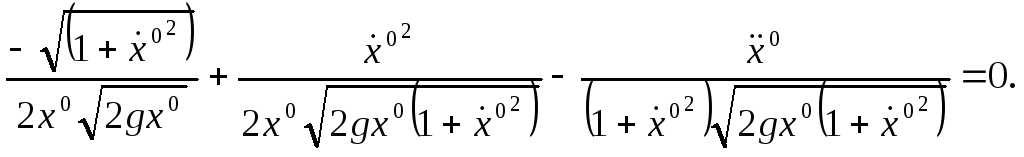
түрінде
жазылады. Осыдан
мұндағы
.
Бұл
дифференциалдық тендеудің шешімі -
циклоида доғасы.
2-мысал.
(Гильберт мысалы).
шарттарында
функционалын
минимумдайық. Бұл
кездегі
Эйлер
тендеуі
,
түрінде
жазылады.
Дифференциалдық
теңдеу шешімін жазайық:
.
Мына
шарттарынан
.
Ендеше
Дегенмен,
функциясы
[0,
1] кесіндісінде
үзіліссіз дифференциалданатын функция
емес.
3 - мысал. (Вейерштрасс мысалы). Айталық
болсын.
Эйлер тендеуінің түрі:
Осы
теңдеу
шешімі:
.
Дегенмен
,
нүктесі
арқылы бұл үйірдің бірде бір қисығы
өтпейді.
Байқайтынымыз: Эйлер тендеуі әлсіз локәлдік минимумның бірінші ретті қажеттілік шартынан алынғандықтан, бірқатар есептер үшін, ол шешім болып табылады. Бірақ келесі жағдайларда кездеседі:
Эйлер тендеуінің жалғыз шешімі бар, бірақ ол әлсіз локәлдік минимумға да, әлді локәлдік миинмумға да жеткізбейді;
шешімдер сансыз көп, және олардың бәрі U -дағы
глобәлдік
минимумын береді; шешімдер сансыз көп, бірақ олардың еш бірі әлді немесе әлсіз локәлдік минимумге жеткізбейді;
Эйлер тендеуінің берілген нүктелер арқылы өтетін бірде бір шешімі жоқ. (3 - мысалды караңыз).
Больц есебі. Мына функционалды минимумдайық:
,
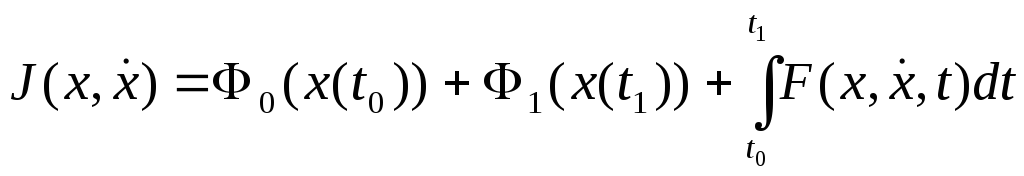(6)
мұндағы
-
бекітілген сандар, ал қарапайым есептен
айырмашылық:
шамалары
бекітілмеген.
1-теорема.
Мәселен
делік
және
айнымалылары
бойынша
екі рет дифференциалданатын болсын.
Онда
функциясы
(6) функционалын әлсіз локәлдік
минимумге жеткізуі үшін ол Эйлер теңдеуін
(7)
мына
(8)
шарттарында қанағаттандыратын шешім болуы қажет.
Дәлелі.
Кейбір
саны үшін
функциясы
шартын
қанағаттандырсын.
Онда (6) - функционал өсімшесінің жазылуы:
мұндағы
,
,
ал
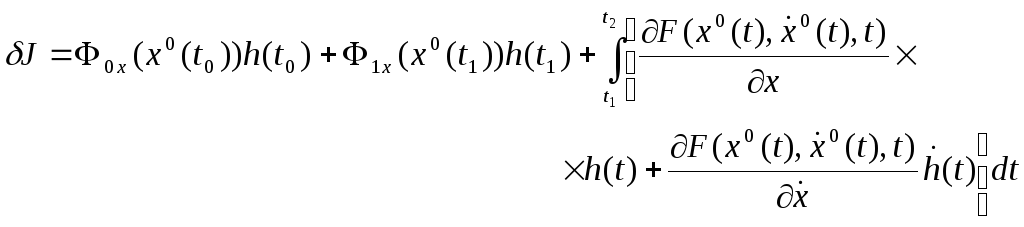
Бөліктеп интегралдау арқылы алатынымыз:
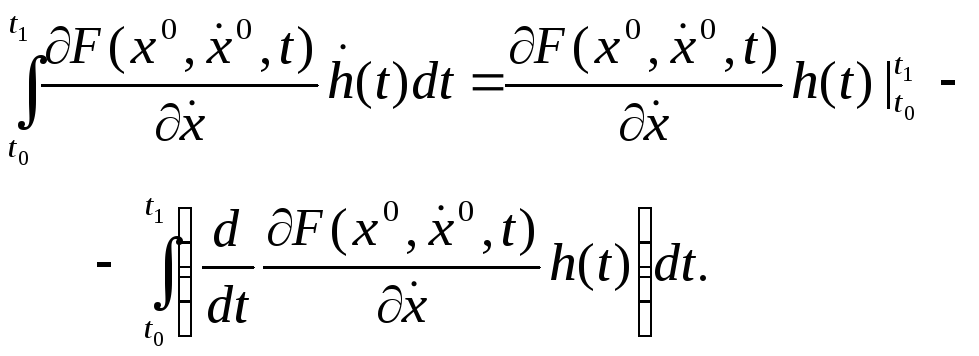
Сонда
вариациясының түрі:
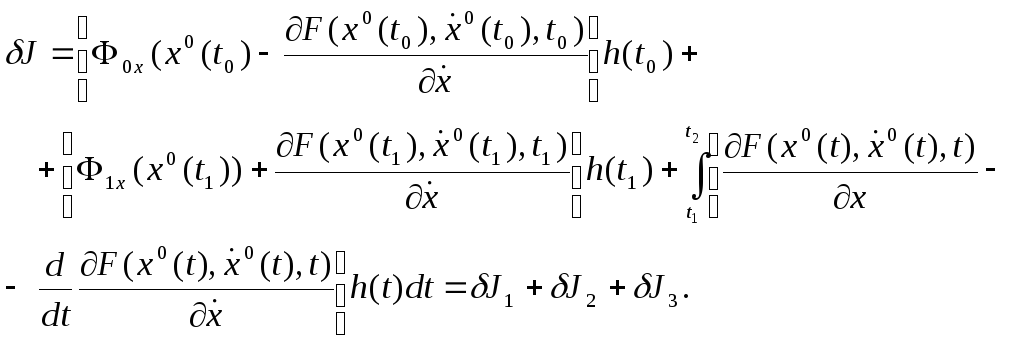
Егер
- (6) - есептің ізделінді шешімі болса,
онда
орындалуы
қажет. Дербес өсімшелер
өзара тәуелсіз болғандықтан
=
0
шартынан шығатыны:
Осыдан
(7), (8) формулалары алынады. Теорема
дәлелденді.
Ескерту:
(7) - тендеу шешімі
функциясы,
тұрақтылары (8) - шарттан анықталады.
Вейерштрастың
қажетті шарты.
Жай есепке оралайық. Әлсіз локәлдік
минимумның қажетгі
шарттары әлді локәлдік минимумның да
қажетті шарттары болатындықтан
функционалды әлді минимумге жеткізетін
функциясы
Эйлер теңдеуінің шешімі болып табылады.
Дегенмен, мұнымен қатар
әлді локәлдік минимумның тікелей
анықтамасынан шығатын қосымша
қажетті шарттар да орындалуы тиіс.
Мұндай
шарт - Вейерштрастың
қажеттілік шарты.
1-анықтама.
Жай есептің Вейерштрасс
фунциясы
деп төрт
айнымалыдан
тәуелді
формуласынан
анықталатын
функциясын
айтамыз.
Ескерту:
егер
функциясы,
бекітілген
кезінде,
айнымалылары бойынша дөңес болса, онда
1-теоремаға орай барлық
үшін
функция
мұндағы
.
2-теорема.
Қарапайым
есепте
функциясы функционалды әлді локәлдік
минимумге жеткізуі үшін Эйлер теңдеуінің
шешімі бойында кез келген
нүктесінде
.
(9)
теңсіздігі орындалуы қажет.
Дәлелі.
Мәселен
функциялары
үшін
,
.
орындалсын дейік. Сонда (9) - өрнек жүзеге асатынын көрсетейік.
Ескерту:
Эйлер тендеуін қорытқан кезде
функциясынын
дербес
жағдайы болып табылатын
функциясын
алғанбыз.