GOS / Krivaya_vtorogo_poryadka

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов отличен от нуля.

Классификация кривых второго порядка

Невырожденные кривые

Кривая второго порядка называется невырожденной, если Могут возникать следующие варианты:

• Невырожденная кривая второго порядка называется центральной, если

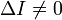
  • эллипс — при услови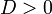и и ;

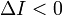    • частный случай эллипса — окружность — при услови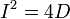и или

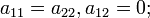
  • мнимый эллипс (ни одной вещественной точки) — при условии

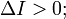
  • гипербола — при условии

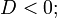
• Невырожденная кривая второго порядка называется нецентральной, если

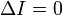
  • парабола — при условии

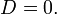
Вырожденные кривые

Кривая второго порядка называется вырожденной, если . Могут возникать следующие варианты:

• вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии

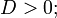
• пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии

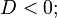
• вырожденная парабола — при условии

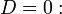
  • пара вещественных параллельных прямых — при условии

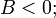
  • одна вещественная прямая (две слившиеся параллельные прямые) — при условии

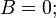
  • пара мнимых параллельных прямых (ни одной вещественной точки) — при условии

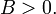
Диаметры и центр кривой второго порядка

Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол с положительным направлением оси Ox, определяется уравнением:

Если выполняется условие то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае () все диаметры кривой либо параллельны, либо совпадают.

Координаты центра определяются системой уравнений:

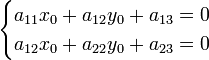
Решая эту систему относительно и получим:

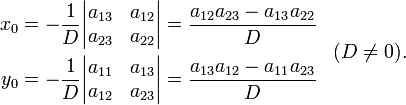
Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду

где  — координаты относительно новой системы.