Симплекс кесте

Базис	C			…		…		…
		b		…		…		…
				…		…		…
…	…	…	…	…	…	…	…	…	…	…
				…		…		…
…	…	…	…	…	…	…	…	…	…	…
				…		…		…
…	…	…	…	…	…	…	…	…	…	…
				…		…		…
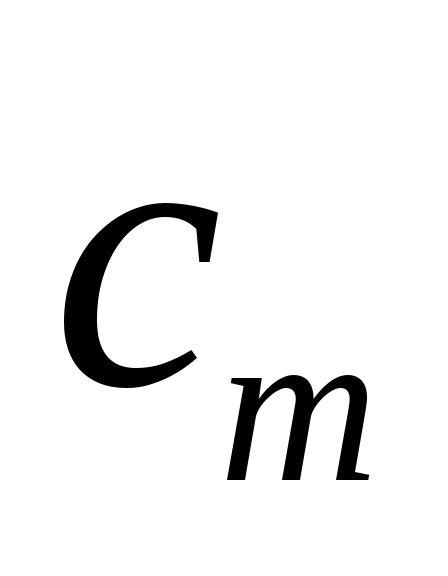
	z			…		…		…
			0	…		…		…

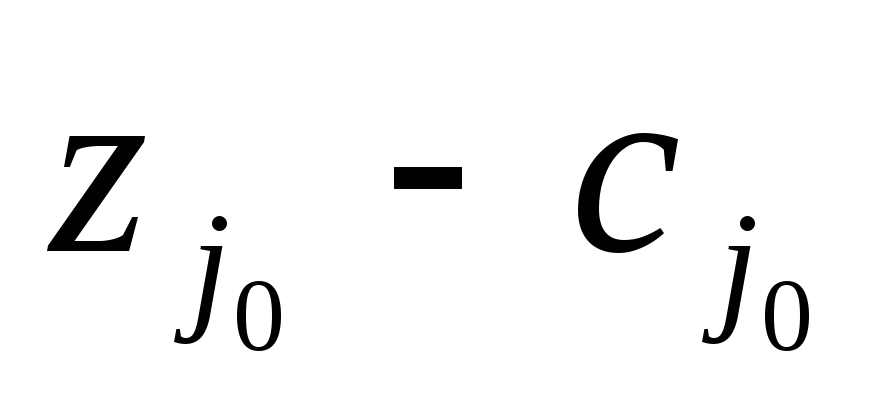
Демек,

Осыдан . Белгілеу енгізейік:. Аңғаратынымыз:өйткені. Онда, мұндағы

Ал болғандықтан . Демек, .

Осы өрнекті тиімділік баламасымен (2) салыстырсақ шеткі нүктесі есептің шешімі болуы үшін мына болуы қажетті және жеткілікті.

Сонымен симплекс кестенің соңғы жолының таңбасына қарап нүктесінің (1),(2) есебінің шешімі болатынын немесе болмайтынын анықтаймыз.

62. Градиенттік әдіс

Градиенттік әдіс. Айталық . Тиімділік есебін қарастырайық

(4*)

Функция , ендеше кез келген векторы үшін

(5)

әрі егер . Скалярлық көбейтінді қасиетінен (Коши-Буняковский теңсіздігінен):

әрі сол жақтағы теңсіздік тек кезінде, ал оң жақтағы кезінде орындалады. Мәселен . Онда (5)-тен шығатыны

мұндағы , егер . Сонымен кезінде функциясының нүктесіндегі ең жылдам кему бағыты (антиградиент) векторының бағытымен беттеседі екен. Дифференциалданатын функцияларды минимумдаудың градиентті әдістерінің бірқатары осы қасиетке негізделген.

Әдіс алгоритмі.

1. Бастапқы нүктесі таңдалады. Бастапқы нүктені таңдаудың жалпы ережесі жоқ.

2. тізбегі

(6)

формула бойынша құрылады.

3. саны градиентті әдіс қадамы деп аталып, шартынан таңдалады:

а) шұғыл түсу әдісінде саны өрнегінен анықталады (мұндағы . функциясы жалғыз айнымалысына тәуелді. Оның минимум жоғарыда баяндалған бір айнымалының функциясын минимумдау әдістерін пайдаланып табамыз;

б) егер Липшиц шартын қанағаттандырса, яғни , онда , саны шартынан (мұндағы - әдіс параметрлері) таңдалады. Дербес жағдайда егер , онда үшін ;

в) тізбегі алдын ала

шарттарымен берілуі мүмкін. Мысалы, . Бұл шақта екендігіне көз жеткізу керек.

г) деп те алуға болады. Егер теңтеңсіздігі орындалмаса (қандай да бір үшін), онда осы теңсіздік орындалғанша санын майдалаймыз (мыс. т.т. дейміз).

Осы санын таңдаумызға сай (4) - есепті шешуді жақсырақ жүзеге асыратын градиентті әдістердің түрлі нұсқаларын аламыз.

ГРАДИЕНТТІК ӘДІС. ГРАДИЕНТ ПРОЕКЦИЯСЫ ӘДІСІ

Градиентті әдіс жалпы жағдайда функциясының -дегі стационар нүктелерін, ал дөңес және әлді дөңес функциялар үшін -дегі глобәлдік минимум нүктелерін табуға мүмкіндік береді.

Градиент проекциясы әдісімен -дегі дөңес жиынындағы функциясының мәндерінің кемімелі тізбегін құруға, ал функциясы дөңес немесе өте дөңес кезінде -дағы -дың глобәлдік минимум нүктесін анықтауға болады.

Градиенттік әдіс. Тиімділік есебін қарастырайық:

, (1)

мұндағы .

1 теорема. Егер , және тізбегі

(2)

ережесімен құрылса, градиент J'(и) Липшиц шартын қанағаттандырса:

(3)

онда

Егер, мұның сыртында, - дөңес, жиыны шектелген болса, онда тізбегі (1) - есеп үшін минимумдаушы болады, яғни

(4)

және кез келген тізбегінің шеткі нүктесі жиынында жатады. Төмендегі бағалау ақиқат:

(5)

Мұндағы . -де әлді дөңес болса

(6)

мұндағы -дегі функциясының әлді дөңестігін білдіретін тұрақты.

Дәлелі. Мәселен , және (2), (3) – шарттары орындалсын. екендігін көрсетейік. Егер қандайда бір ақырғы үшін градиент, онда (2) формуладан , ендеше . Айталық градиент Осы (2) теңдігінің екіншісінен . Онда келесі теңсіздік орындалады

(7)

және градиент (3) шартты қанағаттандырады, онда 1-леммадан (18-дәріс) :

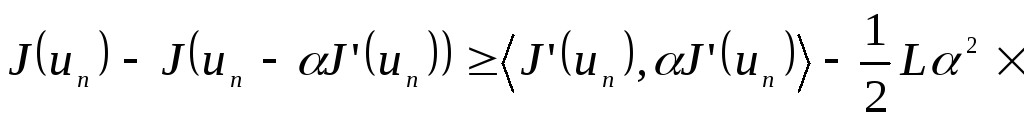
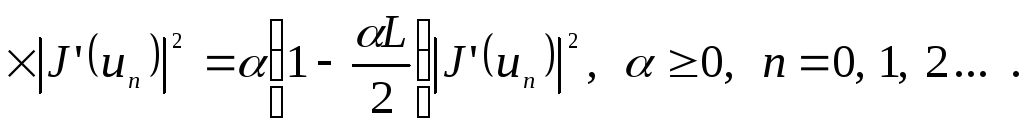(8)

Енді (7) теңсіздігін (8) өрнегін ескере отырып келесі түрде жазамыз

Осыдан

(9)

өйткені кезіндегі , кезінде жетеді. ендеше (9)-дан сандық тізбегінің қатаң кемитінін көреміз .

, онда сан тізбегі төменнен шектелген, демек шегі бар болып, кезінде . Шекке кезде көшіп (9)-дан алатынымыз . Теореманың бірінші бөлімі дәлелденді.

Мәселен, көрсетілген шарттардың сыртында, - дөңес функция және жиыны шектелген болсын. Сонда (2) -дегі тізбегі минимумдаушы болатынын көрсетейік. -дегі үзіліссіз болғандықтан жиыны тұйық. Шындығында да егер – жиынының шекті нүктесі болса, онда кезінде тізбегі табылады. тиістілігінен . Осыдан шекке көшіп, үзіліссіздігін ескеріп алатынымыз: . Демек .

Сонымен, - шектелген тұйық жиын, демек ол - компакт Ескерту: сан тізбегі қатаң кемігендіктен демек . Екінші жағынан, үзіліссіз функция компакт жиынында өзінің төменгі мәніне жетеді. Сондықтан , яғни . Атап өтетініміз: компакт 2-теоремаға орай дөңес жиын.

Дөңес функция , - дөңес жиын, онда келесі теңсіздіктің (4-дәріс 1-теорема) орындалуы қажетті және жеткілікті

Осыдан

(10)

(10) - нан дербес жағдайда кезінде алатынымыз

(11)

мұндағы - жиынының диаметрі. , онда (10)-нан . Бұл тізбегі минимумдаушы екенін, онымен қоса оның кез келген нүктесі жиынында жататындығын білдіреді, - компакт жиын, - -де үзіліссіз. (4)-өрнектің әділдігі дәлелденді. Енді (5) бағасының дұрыстығын дәлелдейік. Белгілеу: . Енді (9), (11) теңсіздіктері былай жазылады:

(12)

Осы (12) өрнегінен көретініміз: , себебі . Әрі қарай 2-лемманы қолдансақ (5)- бағаны аламыз, мұндағы .

Ақырында, (6) өрнекті дәлелдейміз. - әлді дөңес функция. Бұл жағдайда 4-дәрістегі (7), (8) теңсіздіктері орындалады (4, 5 - теоремалар). минимум нүктесінде теңсіздігі орындалуы қажетті және жеткілікті болғандықтан 4-дәрістегі (8)-өрнектен кезінде

. Осыдан

(13)

Мына мәні үшін (13) теңсіздігінен . Осымен (11) теңсіздігінен . онда , өйткені . Бұдан (мұндағы ). Әрі қарай мыналарды , ескеріп (6) бағасын аламыз. Теорема дәлелденді.

Градиенттер проекциясы әдісі. Тиімділік есебін қарастырайық

(14)

мұндағы , - дөңес тұйық жиын.

Әдістің алгоритмі.

1. Бастапқы нүкгесі таңдалады.

2. нүктесі анықталады;

3. нүктесінің жиынындағы проекциясын тауып, нәтижесінде

нүктесін анықтаймыз. Жалпы жағдайда тізбегі мына ереже бойынша құрылады:

(15)

мұндағы саны шартынан таңдалады. Бұл санын таңдаудың түрлі тәсілдері бар, оның кейбіріне жоғарыда тоқталғанбыз.

2 - теорема. Егер функция - дөңес тұйық жиын, градиент Липшиц шартын қанағаттандырады және тізбегі (15) - формуладан анықталса (мұндағы - берілген сандар ), онда - да .

Егер, мұның сыртында, , - да дөңес, жиыны шектелсе, онда тізбегі (14) есебінің минимумдаушы тізбегі және оның кез келген шеткі нүктесі жиынында жатады. Мына бағалау ақиқат

(16)

мұндағы - жиынының диаметрі.

Дәлелі. нүктесі нүктесінің проекциясы, онда

5-теоремадан алатынымыз , (6)- формуланы қараңыз ):

Осыдан

(17)

1-леммаға сай (2 - формула)

(18)

Осы (17), (18) өрнектерінен теңсіздіктерін ескеріп

(19)

екенін аламыз.

Бұл (19) өрнегінен сан тізбегі қатаң кемитінін, ал болғандықтан оның жинақталатынын демек -да

көреміз. Ендеше (19) - дан , . Теореманың бірінші бөлімі дәлелденді.

Енді, аталған шарттар сыртында, функциясы - да

дөңес делік, онда шектелген және тұйық жиын, яғни ықшам. Мұнымен қоса , , функциясы төменгі қырға жиынына жетеді (1- теореманың дәлелдеуін қараңыз) делік. тізбегінің минимумдаушы екендігін көрсетейік. (11) –формуладан

(20)

(17)-өрнектен мына теңсіздік орындалатынын көреміз

(21)

Сонда (20) мен (21)-ден:

.

Осыдан

екендігін ескерсек . Дәлелдеуіміз бойынша , демек . Бұл тізбегі минимумдаушы екендігін және жиынының компакттығы мен функциясының үзіліссіздігінен барлық шеткі нүктелері жиынында жататындығын білдіреді.

теңсіздіктерінен шығатыны . Осыдан 2-лемма негізінде (16) бағасын аламыз. Теорема дәлеленді.

Ескерту: градиент проекциясы әдісі U жиынында v= нүктесінің проекциясын анықтауды талап етеді. Жалпы жағдайда оны шешу - өте күрделі мәселе. Сондықтан бұл әдісті нүктесініңU жиынындағы проекциясы оңай анықталатын жағдайларда қолданған жөн.

ШАРТТЫ ГРАДИЕНТ ӘДІСІ. ТҮЙІНДЕС ГРАДИЕНТТЕР ӘДІСІ.

Шартты градиент әдісімен дөңес функциясының -дегі дөңес тұйық U жиынындағы минимумын табуға болады. Түйіндес градиенттер әдісін квадратты функцияларды минимумдау үшін пайдаланған жөн. Егер квадратты функция дөңес болса түйіндес градиенттер әдісі минимумының нүктесінеn - нен аспайтын қадамда жинақталады.

1. Шартты градиент әдісі. Тиімділік есебін қарастырайық:

(1)

мұндағы ,U - -дегі шектелген тұйық дөңес жиын.

Әдіс алгоритмі.

1. Бастапқы нүктесі таңдалады. Байқаймыз:

2. Мына тиімділік есебінің

шешімі ретіндегі көмекші нүктесі анықталады. Сонымен

3. Келесі жуықтау .U -дөңес жиын , ендеше . Жалпы жағдайда

(2)

мұндағы . U -компакт, -сызықты функция, онда нүктесі табылады.

1-теорема. Егер функция ,U - тұйық шектелген дөңес жиын, градиент Липшиц шартын қанағаттандырып және тізбегі (2) - формуладан анықталып, саны

(3) шартынан анықталса, онда

,. (4)

Егер, мұның сыртында, U -да дөңес болса, онда тізбегі (1) - есеп үшін минимумдаушы болады және оның кез келген шекті нүктесі жиынында жатады. Келесі баға ақиқат:

(5)

мұндағы .

Дәлелі. U - компакт, , онда.U шектелгендіктен оның диаметрі . (3) шарттан . Онда, 1-леммаға орай

(6)

мұндағы ,өйткені .

Егер , онда теореманың бірінші бөлімі дәлелденді. (6) өрнектен:

(7)

Ескерту: , онда. Себебі, ендешетеңсіздігі орындалады. Демек болғандықтантізбегі өспейді. Осыданжинақталады, яғни, . Енді - да шекке көшіп, (7)-ден алатынымыз

Осыдан да, .

(4) -өрнектің дұрыстығы дәлелденді. Теореманың бірінші бөлімі дәлелденді.

Мәселен, аталған шарттар сыртында, функциясыU –да дөңес делік. Бұл жағдайда да алдыңғы теоремалардын дәлелдеуіндегідей келесі теңсіздік орындалары хақ:

(8)

Осыдан, дәлелдегеніміз бойынша : . Бұл тізбегінің минимумдаушы екенін білдіреді.

(5)-баға дұрыстығын көрсетейік. (6) мен (8) бағаларынан

(9)

Ескерту: функциясыныңбойынша максимумыкезінде болады,әрі , өйткені-да.мәнін қойып, (9)-дан алатынымыз

(10)

Сонғы (10) -нан көретініміз: . Онда 2-леммаға сай барлықүшін. Осыдан барлықкезінде (5) бағасы ақиқат болатын тұрақтысы табылады. Теорема дәлелденді.

Түйіндес градиенттер әдісі. Квадратты функцияның -дегі минимум іздегенде градиентті әдіске қарағанда түйіндес градиенттер әдісі неғұрлым ұтымды әдіс болып табылады. Түйіндес градиенттер әдісін тегіс функциялар минимум нүктесінің аймағында қолданған жөн, себебі минимум нүктесінің аймағында бастапқы функцияны жеткілікті дәлдік дәрежесінде квадратты функцияға жуықтатуға болады.Келесі есепті қарасгырайық:

(11)

мұндағы .

Әдіс алгоритмі.

1. Бастапқы нүктесі таңдалады.

2. тізбегі

(12)

(13)

ережесіне сай құрылады.

Сандық тізбектер былай таңдалады:

(14)

(15)

мұндағы индекстер жиындары , шартынан таңдалады. Дербес жағдайда егер, онда барлықn, u кезінде шұғыл түсу әдісін аламыз. Индекстер жиынынтаңдауға байланысты түйіндес градиенттер әдісінің түрлі нұсқаларын аламыз.

Бұдан былай түйіндес градиенттер әдісін

(16)

функциясы үшін қарастырамыз, мұндағы - ретті оң анықталған симметриялы матрица, - берілген вектор. (16) функцияеы үшін (12)-(15) өрнектерінен анықталатын тізбектері былай жазылады:

1)

онда саны ( мұндағы)

(17)

формуласынан анықталады. Шынында да үшін скалярлық көбейтінді. Байқайтынымыз: . Дәлелдеуі төменде келтіріледі (лемманы қараймыз)

2) , онда

. Демек

(18)

Лемма. Егер индекстер жиыны , онда (12) - (14) формулаларынан анықталатын тізбегі (16) -дағы функциясы үшін

(19)

шарттарын қанағаттандырады.

Дәлелі. екенін көрсетейік. Математикалық индукция әдісін қолданамыз. үшін алатынымыз

(20)

мұндағы . (17) - өрнектегі бірінші теңдіктен .

мәнін (20) - өрнектің оң жағына қойсақ . Айталықтендігі қандай да бірүшін орындалсын. Бұл үшін де ақиқат екендігін көрсетейік. Байқайтынымыз әрі . Онда

өйткені

.

Егер , онда ,

демек . Сонымен

(21)

теңсіздігінің ақиқаттығы дәлелденді.

(21) - формуладан шығатыны

(22)

Осы (21), (22) теңдіктерінің негізінде

(23)

екенін анықтаудың қиындығы жоқ.

(19)-теңсіздігін дәлелдейік. Математикалық индукция әдісін қолданамыз. кезінде теңдігін жоғарыда дәлелдегенбіз, ал өрнегі (18)-ден шығады. Мәселен (19) теңдігі барлық үшін орындалсын делік. Сонда олар үшін де дұрыстығын көрсетейік, (21) - (22)-ден тікелей кезінде. онда кезінде

(24) (индукция ұйғарымы бойынша). Ендеше (24) негізінде

Скалярлық көбейтінді

себебі ( жағдайы). Ақырында, (18) негізінде . Сонымен

Лемма дәлелденді.

2-теорема. Егер индекстер жиыны онда тізбегі (16) - дағы функциясы бар (11) есебі үшін минимум нүктесіне n -нен аспайтын қадамда жинақталады.

Дәлелі. Леммаға сай векторлар ортогонәлді.-дегі мұндай нөлден ерекше векторлар саны n-нен аспайды. Демек, болатын нөмірі табылады. Бұл екенін білдіреді, өйткені дөңес функция. Теорема дәлелденді.