Функционал мәнін есептейік
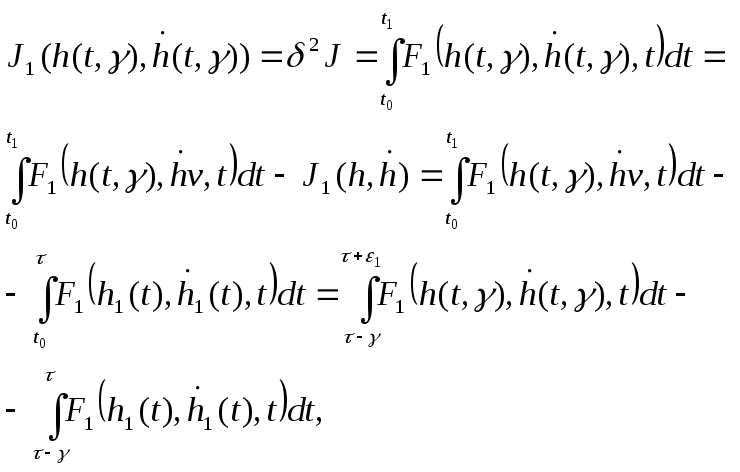(7)
мұндағы
((6)-формулаға орай) және
.
Ескерту:
туынды
ортасы
туралы теоремадан
.
Онда
(7) - формуладан, интеграл ортасы
туралы теоремадан
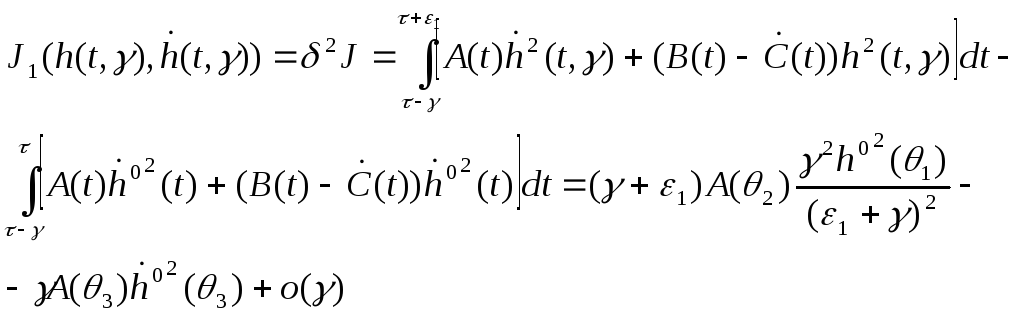
мұндағы
.
Байқаймыз:
әрі
,
ал туынды
.
Демек
кезінде
болатын
сандары
табылады. Бұл
шартына
қайшы. Есептеу ретінің түзіктігі үшін
Лежандр теоремасын дәлелдегендегідей
функциясын
нүктелерінде тегістеу қалды.
Теорема дәлелденді.
n БЕЛГІСІЗ ФУНКЦИЯЛАРДАН ТӘУЕЛДІ ФУНКЦИОНАЛДАР.
Жай
есепті
вектор
функция жағдайында қарастырайық. Сонымен
келесі функционалды
минимумдайық.
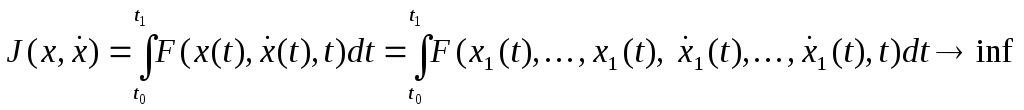(8)
.
(9)
Біз
белгілеуін
енгізіп, (8),(9) есебін
түрінде жазамыз.
3-теорема.
функциясы
U
-да
функционалын әлсіз локәлдік минимумге
жеткізуі үшін ол Эйлер теқдеуінің
.
(10)
шешімі болуы қажет.
Дәлелі.
Ұйғарымды
вектор функция таңцап алайық
.
бұл
кезде
.
Онда
функционалдың
бірінші вариациясы
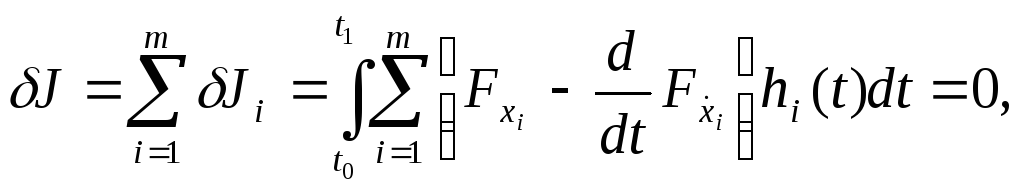
мұндағы
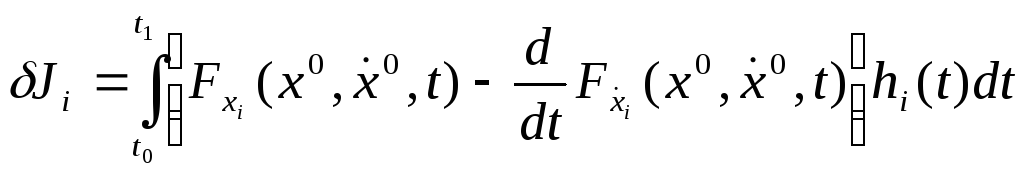. (11)
Жоғарыдағы
өсімшелері өзара тәуелсіз, ендеше
шартынан
.
Онда (11)-ден
Лагранж леммасынан Эйлер тендеуін (10)
аламыз. Теорема дәлелденді.
Ескерту:
(11)-
ретті
дифференциалдық тендеу оның шешімі
;
тұрақтылары
шарттарынан
анықталады.
ЖОҒАРҒЫ РЕТТІ ТУЫНДЫЛАРДАН ТӘУЕЛДІ ФУНКЦИОНАЛДАР.
Келесі есепті қарастырайық:
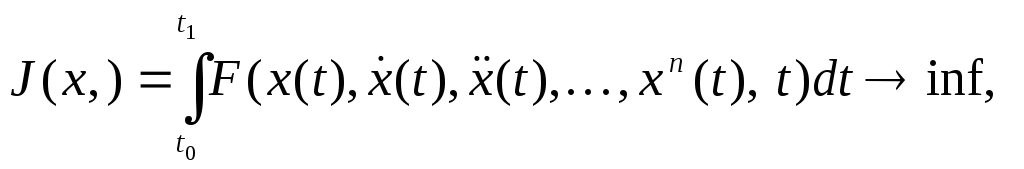(12)
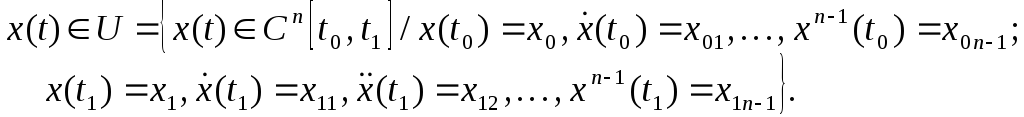(13)
4-теорема.
функциясы (12) функционалын (13) шартында
әлсіз локәлдік минимумге жеткізуі үшін
оның Эйлер-Пуассон
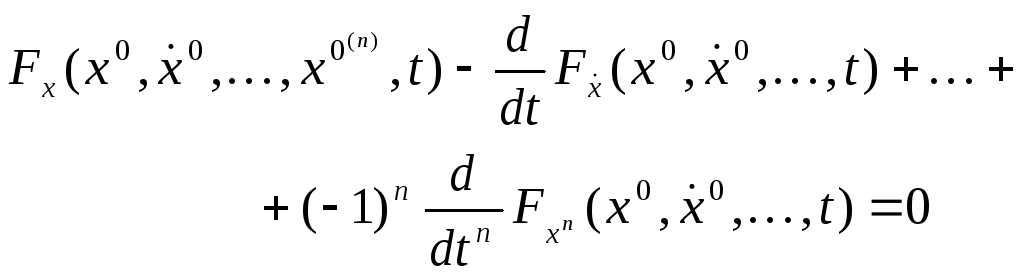(14)
тендеуінің шешімі болуы қажет.
Дәлелі.
,
яғни
функциялары
үшін бөліктеп интегралдаған соң
функционалдың бірінші вариациясы
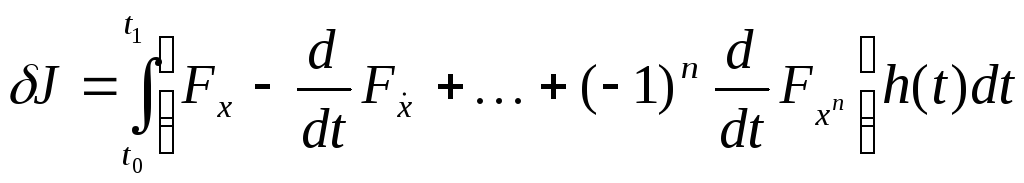
түрінде
жазылады. Сонда
шартынан
Лагранж леммасына орай (14)-тендеу
алынады. Теорема дәлелденді.
Ескерту:
(14)-
ретті дифференциалдық тендеу, ал оның
шешімі
;
тұрақтылары
шарттарынан
анықталады.
65. Изопериметрлік есеп. Шартты экстремум
Бұл дәрісте изопериметрлік есепті және шартты экстремум есептерін шешудің әдістері келтірілген. Лагранждың жалпы есебі үшін бірінші ретті қажеттілік шарты қисындалған. Жалпы ескертпелерде қысқаша Гильберт шарты мен экстремәлдардың сыну нүктелеріндегі Вейерштрасс-Эрдман қажетті шарттары баяндалған.
Изопериметрлік есеп. Келесі есепті изопериметрлік есеп дейміз:
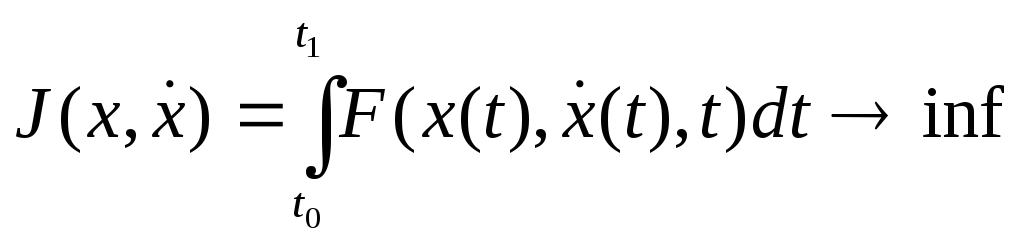(1)
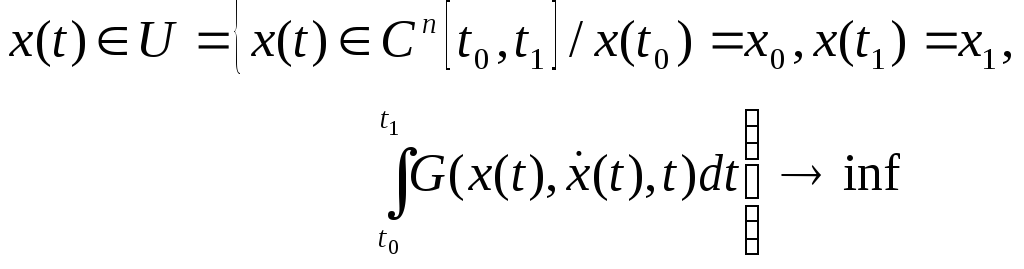(2)
мұндағы
аймағында
екі рет
дифференциадданатын
функциялар, l
- берілген сан.
1-теорема.
Егер
функциясы
(1) функционалды (2) шарттарда әлсіз
локәлдік экстремумге жеткізсе және ол
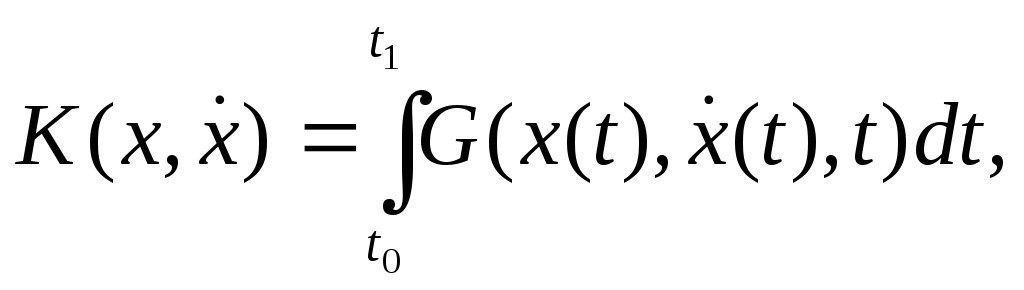(3)
функционалының
экстремәлі болмаса, онда
функциясы
(4)
дифференциалдық
тендеуінің шешімі болатын
саны табылады.
Дәлелі.
нүктелерін
таңдап
алайық.
Мәселен
,
мұндағы
–
U
-дағы функционалдың
әлсіз локәлдік минимум нүктесі, ал
Сондағы (1) - функционалдың өсімшесі
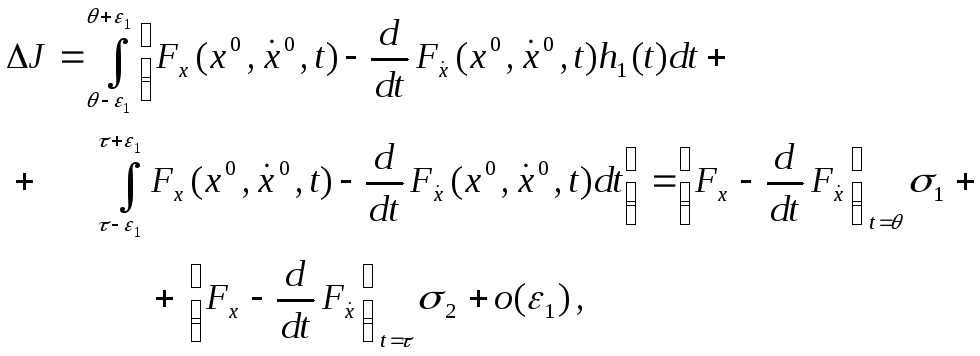(5)
мұндағы
.
Байқаймыз:
реттері
,
яғни
.
ендеше
демек
(6)
Теорема
шартынан
функциясы
(3) функционалының
экстремәлі
емес, демек
нүктесін
болатындай
етіп
тандауға болады. Сонда (6)-дан:
(7)
(7)-дегі
мәнін (6) өрнектің оң жағына қойсақ:
(8)
мұндағы
сан.
Сонымен (8) түріндегі
функционал
өсімшесін қорытқанда
шарты
ескерілген, яғни ол қарапайым жағдайдағыдай
функция өсімшесі, демек
Осыдан (4) - өрнек алынды. Теорема дәлелденді.
Байқайтынымыз:
(4) шарты екінші ретті дифференциалдық
тендеу және оның шешімі
,
түрақтылары
шарттарынан анықталады. Жалпы жағдайда
изопериметрлік есеп былай қисындалады:
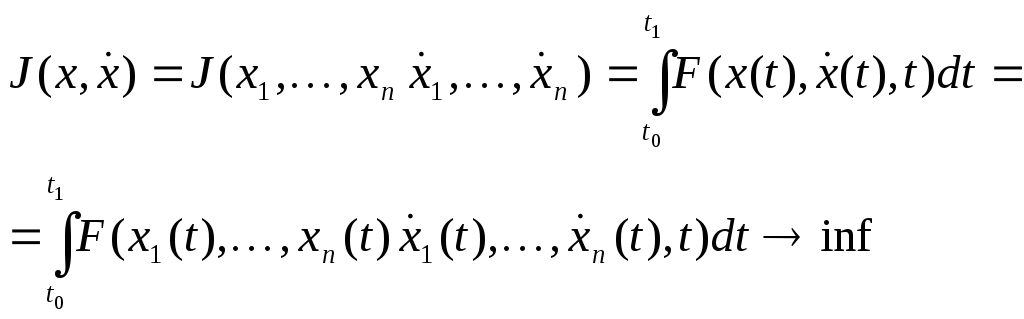(9)
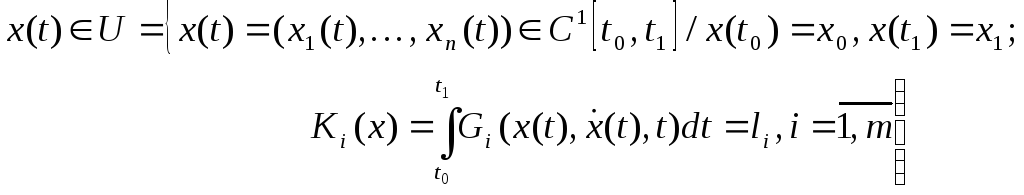(10)
2-теорема.
Егер
вектор функциясы (9) функционалын (10)
шарттарда әлсіз локәлдік минимумге
жеткізсе, онда вектор функция
келесі
тендеулердің
, (11)
шешімі
болатын, барлығы бірдей нөлге тең емес
сандары
табылады. Мұндағы
функциясы лагранжиан деп аталып,
формуласымен анықталады.
Теорема
жағдайы
үшін жоғарыда дәлелденген. Жалпы жағдай
үшін ұқсас
тәсілдермен дәлелденеді.
Ескерту:
(11) -тендеу шешімі
вектор
функциясы, ал
тұрақтылары
шарттарынан
анықталады.
Шартты экстремум. Келесі Лагранж есебін қарастырайық:
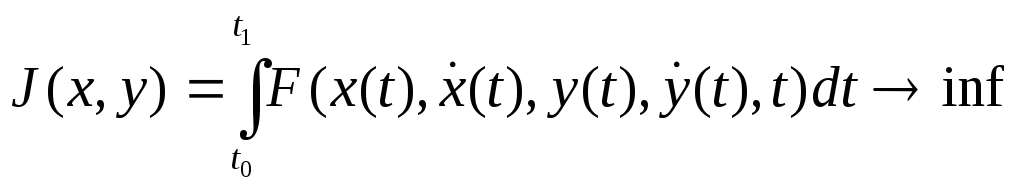(12)
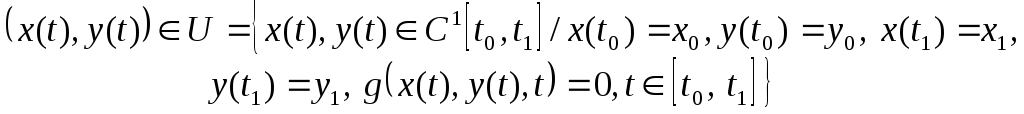(13)
Басқаша
айтқанда
функционалын
берілген
бетіндегі
үзіліссіз
дифференциалданатын функциялар жиынында
минимумдау керек.
3-теорема.
Егер
функциясы (12) функционалын (13) шарттарда
әлсіз локәлдік минимумге жеткізсе және
мен
туындылары бір мезгілде нөлге айналмаса,
онда
функциясы
(14)
(15)
дифференциалдық
тендеулерінің шешімі болатын
функциясы
табылады.
Дәлелі.
Мәселен
,делік
(мұндағы
).
Сондағы
(12) - функционал өсімшесі
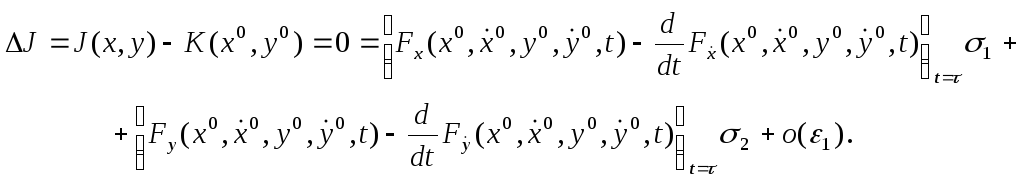(16)
мұндағы
- жеткілікті
аз сан,
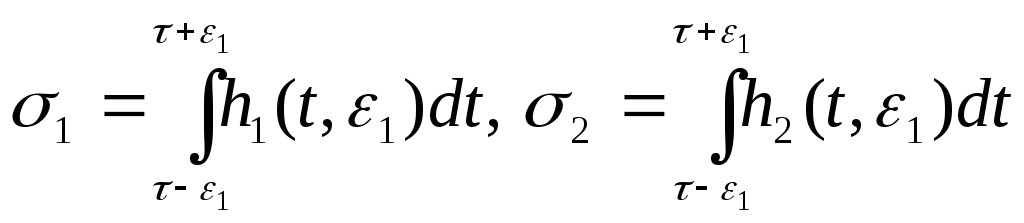әрі
сандары оң да теріс те болуы мүмкін,
екеуі де
ретті,
яғни
.
,ендеше
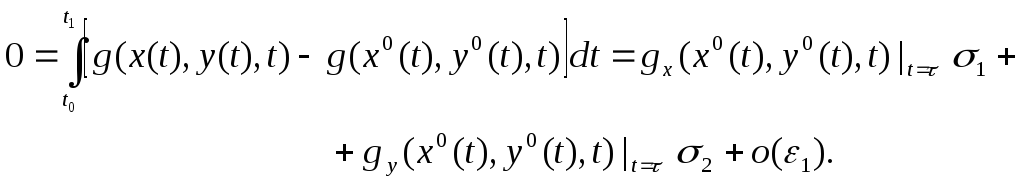
Осыдан
(16) - өрнектің оң жағына мәнін
қойсақ: қарапайым есептегі сияқты (12)-(шектеуін ескере отырып) функционалының өсімшесін аламыз:
Осыдан
және әлсіз локәлдік минимумның қажетті
шартынан
:
(17)
Белгілеу
енгізсек:
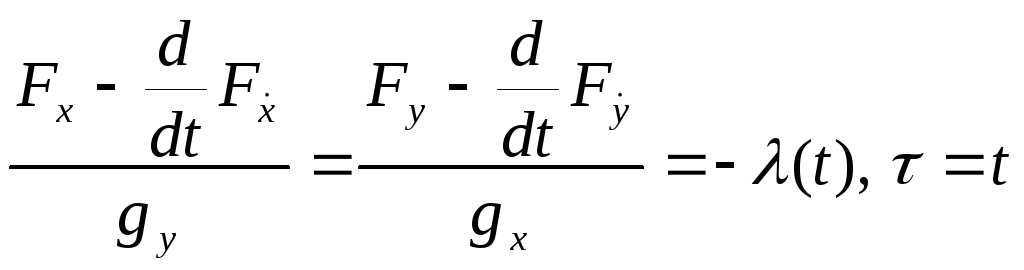
(17)-ден (14), (15) дифференциалдық теңдеулерін аламыз, Теорема дәлелденді.
Лагранж есебі шартты экстремум есебінің жалпылануы болып табылады:
(18)
(19)
(20)
мұндағы
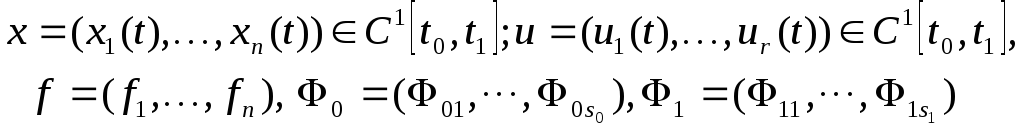
кезіндегі айнымалылар бойынша үзіліссіз дифференциалданатын функциялар.
Жоғарыда қарастырылған барлық есептер (18)-(20) есептерінің дербес жағдайлары. Шындығында да қарапайым есепті
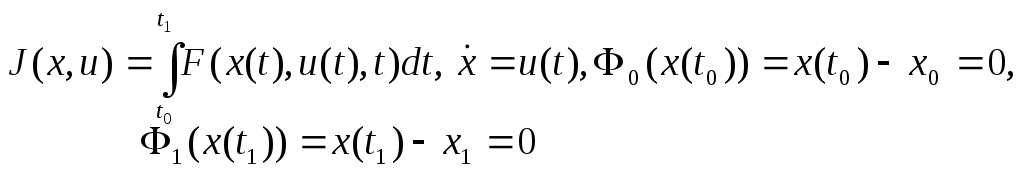
түрінде жазуға болады.
Изопериметрлік есептің жазылуы:
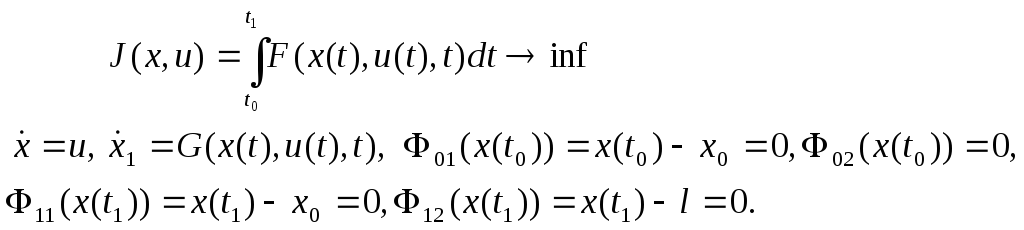
(18)-(20) есебі үшін функция
лагранжан деп, ал функционал
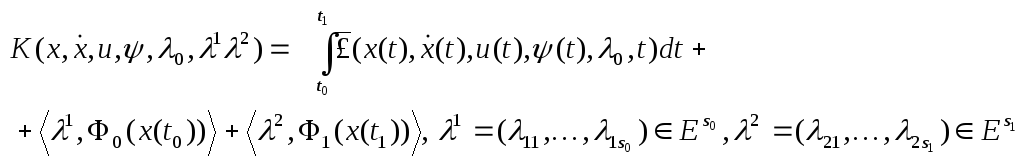
Лагранж функционалы деп аталады.
4-теорема.
Мына жұп
(18) – (20)
есебін локәлдік минимумге жеткізуі
үшін
келесі
шарттарды қанағаттандыратын
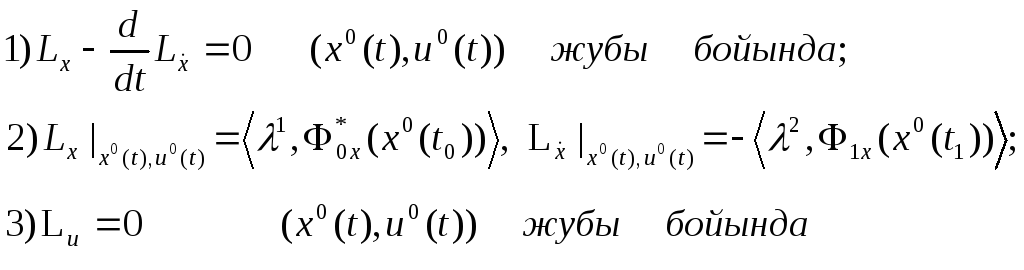
барлығы
бірдей нөл
емес
Лагранж көбейткіштері
табылуы
қажет.
4-теореманың дербес жағдайлары жоғарыда дәлелденген, ал теореманың неғұрлым жалпы жағдайлары келесі тарауда дәлелденеді.
Жай есептің жалпы ескертпелері.
Жоғарыда көрсетілгендейжай есеп үшін Эйлер теңдеуі
Осы тендеуді
(21)
түрінде жазуға болады.
Бұдан
аңғаратынымыз:
функциясының
класында
ізделінетініне қарамастан Эйлер тендеуі
функциясын
анықтауға келтіріледі. Онда ізделінді
функция қашан
болады
деген сұрақ туады. Алғашқы үш қосылғыш
бойында
бойынша үзіліссіз, ендеше
табылуы
үшін
орындалуы
қажет. Бұл шартты
Гильберт
шарты дейді.
2)
Кейде
функцияларының
туындылары оқшауланған
нүктелерде
(
кесіндісіндегі)
бірінші ретті үзілісті болуы мүмкін.
Бұл жағдайларда
нүктелерінің арасында
функциясы
Эйлер теңдеуін
қанағаттандырады және сыну
нүктелерінде
(22)
шарттары
орындалады.
-
ден алынатын (22) шарты Вейерштрасс-Эрдман
шарты деп аталады.
функциясының
бойындағы
үзіліссіздігі Эйлер теңдеуінің
шешімдерін
нүктелерінде
түйістіру үшін, яғни (7)-Эйлер тендеуінің
жалпы шешімдегі
тұрақтыларын
анықтау үшін қолданылады.