Енді конусы (22) - формуладан анықталғандықтан

Осыдан (7) өрнектің ақиқаттығын көреміз. Барлық нөлге тең еместігінен тікелей (6) шарт шығады. Байқайтынымыз: егер қандай да бір i, үшін онда конус демек . Бұдан . Ендеше . Сонымен , яғни (8) шарт орындалып тұр. Теорема дәлелденді.

СЫЗЫҚСЫЗ ПРОГРАММАЛАУЬЕСЕБІН ШЕШУ АЛГОРИТМІ

Сызықсыз программалаудың келесі есебін шешудің тәртібін көрсетейік:

, (1)

, (2)

мұндағы ал - ашық, дегі дөңес жиынын қамтитын жиын, дербес жағдайда алдыңғы лекциядағы (6)-(8) өрнектерінің негізінде . Ескерту: (6)-(8) шарттары тек нүктесі ғана емес сонымен қатар жиынындағы функциясының локәлдік минимум нүктелері үшін де орындалады. Қандай шарттар орындалғанда (1) - (2) есебі ерекшеленбеген болады және U - дағы - дің локәлдік минимум нүктесі деген сұраққа жауап берейік.

1 . Әуелі екендігіне көз жеткіземіз. Ол үшін Вейерштрасстың теоремаларына сүйенеміз.

2. (1) - (2) есебі үшін жалпыланған Лагранж функциясын құрамыз

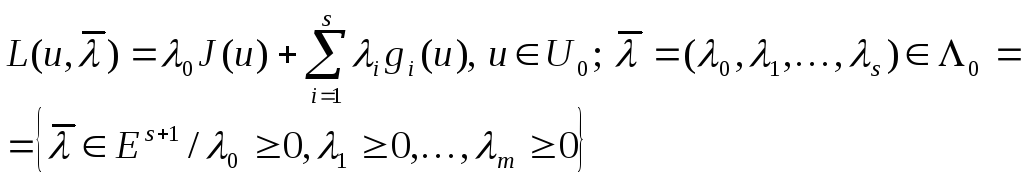
_3.

, (3)

(4)

(5)

шарттарынан нүктелерін табамыз, мұндағы - берілген сан, дербес жагдайда .

а) Егер немесе , онда (4) шартын алмастырамыз:

. (6)

Бұл жағдайда түріндегі белгісіздерді анықтау үшін ((3), (6), (5)) алгебралық теңдеулердің жүйесін аламыз.

б) Егер алгебралық теңдеулерді ((3), (5), (6)) немесе (3) - (5) жүйелерін шешкен соң болса, онда (1) - (2) есебі ерекшеленбеген деп аталады. Ерекшеленбеген есептегі (3) шартты неғұрлым қарапайым шартымен алмастыруға болады. Егер ерекшеленбеген есептегі жұбы

Лагранж функциясының қайқы нүктесі болса, онда глобәлдік минимум нүктесі.

4. Сызықсыз программалаудың келесі есебін қарастырайық

(7)

(8)

Бұл (7), (8) есебі (1)-(2) есебінің дербес жағдайы. .Егер векторлары сызықты тәуелсіз болса, онда (7) - (8) есебіндегі нүктесі қалыпты минимум нүктесі делінеді. Ескерту: егер қалыпты нүкте болса, онда (7) - (8) есебі ерекшеленбеген есеп болғаны. Шынында да (7) - (8) есебі үшін

(9)

тендігі орындалады. Егер мұндағы , онда векторларының сызықты тәуелсіздігінен алатынымыз: .Сонда . Бұл (З)-ке қайшы.

(7)- (8) есебінің қалыпты нүктесі делік. Онда деуге болады да Лагранж функциясы түрінде өрнектеледі.

ТЕОРЕМА. Мәселен функциялары нүктесінің аймағында анықталған, және екі рет дифференциалданатын болсын.

нүктесі жиынындағы функциясының локәлдік минимум нүктесі болуы үшін, яғни орындалуы үшін

квадраттық формасы

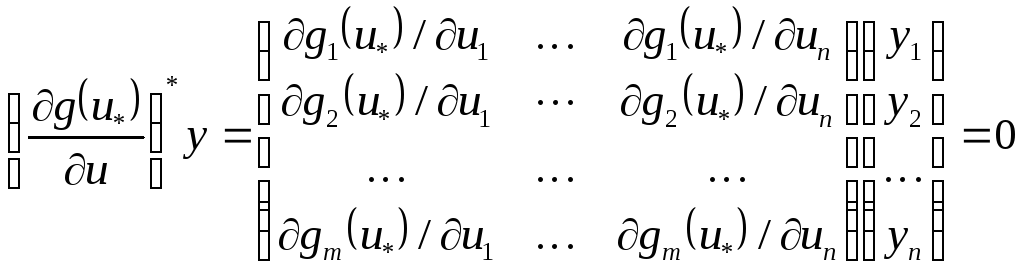(10) гипержазықтығында оң анықталуы қажет.

Дәлелі. Айталық квадраттық форма (10)-гипержазықтығында оң анықталсын

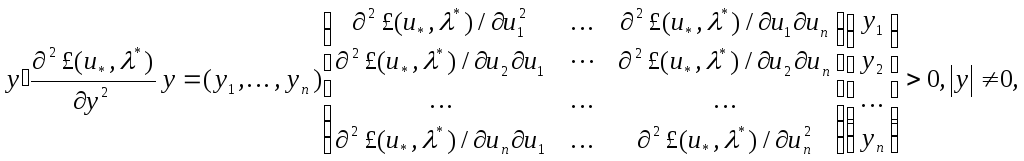
нүктесі функциясының U жиынындағы локәлдік минимум нүктесі екендігін көрсетейік. Байқайтынымыз: - қалыпты нүкте және ол , яғни шартынан анықталады. Сонымен жұбы - белгісіз. шарттары белгілі, ендеше үзіліссіз функциясы у айнымалысына қатысты компакт жиынында төменгі мәнге жетеді. саны делік. Мына жиынды енгізейік

, (11)

мұндағы * - транспозициялау белгісі. - жеткілікті аз сан. Егер , онда квадраттық форма

(12)

мұндағы ((11) шартты еске алыңыз) нүктелері үшін

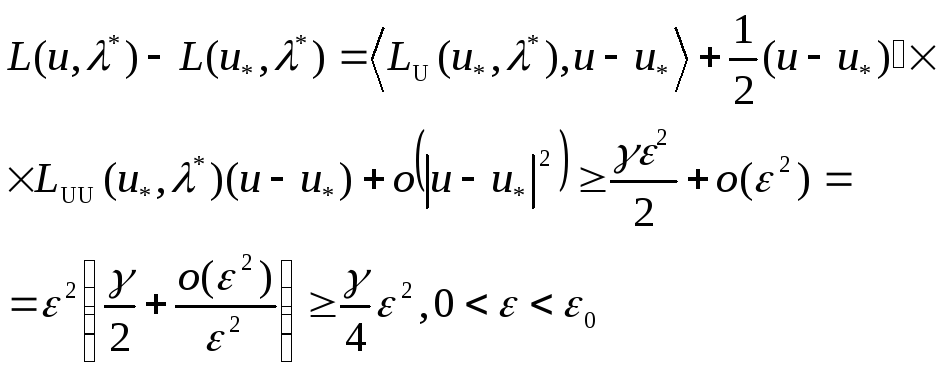(13)

болғандықтан (12) теңсіздік пен кезінде орындалады. Мына жиынды енгізейік:

. (14)

(10) гипержазықтығы бернесіне нүктесіне жанама болғандықтан, әрбір нүктесі үшін норма болатын нүкте табылады. Шынында да, егер

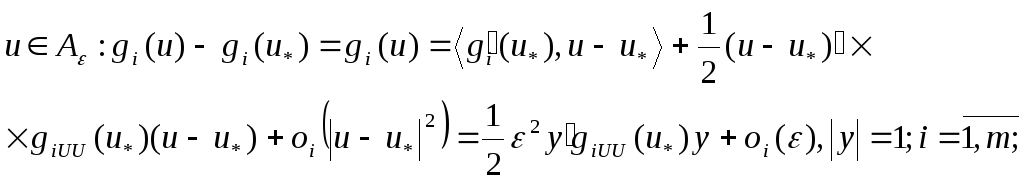(15)

(16)

(11), (14), (15), (16) өрнектерінен шығатыны

функциясы нүктесінің аймағында бойынша үзіліссіз -дифференциалданатындықтан және туынды , ендеше нүктесінің аймағындағы айырма

Осыдан дербес жағдайда егер - жеткілікгі аз сан

, нүктелері үшін

демек норма ( жеткілікті аз кезінде):

Онда мына айырма (13) өрнегіне сай:

'(17)

, себебі , ендеше (17) - ден алатынымыз . Демек, жиынындағы функциясының локәлдік минимум нүктесі. Теорема дәлелденді.

Мысал. Айталық ,. U жиынылдағы функциясының минимум табу керек. Осы мысалдағы , . компакт жиын болғандықтан . Тиімділіктің қажетті шарттары:

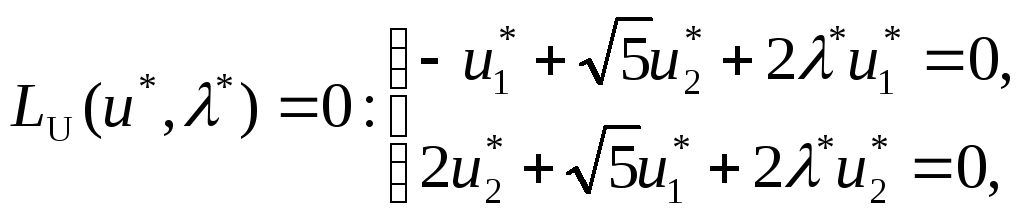
мұндағы .

Осыдан нүктелерін табамыз:

Осы 1) - 4) арасындағы қандай нүктесінде функциясыжиынындағы минимуміне жетеді?

Оны анықтау үшін әуелі - дағы минимуміне функциясының локәлдік минимумге жететін нүктелерін екшеп аламыз. Байқайтынымыз: есеп ерекшеленбеген және матрицасы мен векторы мынаған тең:

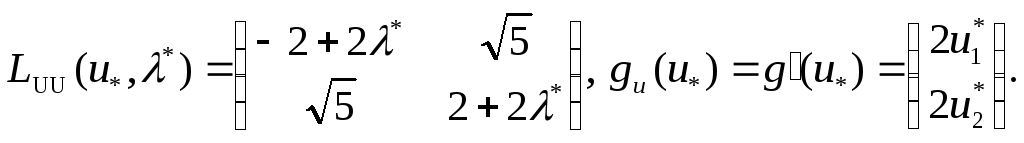
Бірінші нүкте үшін квадраттық форма

гипержазықтығының теңдеуі. Осыдан алатынымыз . Мына мәнін квадраттық формаға қойсақ . Демек, .- дағы функциясының локәлдік минимум нүктесі. Дәл осылайша локәлдік минимум нүктесі, ал , нүктелері локәлді минимум нүктесі емес екендігіне көз жеткізуге болады. - дағы минимум табу үшін 1) мен 2) нүктелеріндегі функциясының мәндерін есептейміз. екенін көрсетуге болады.

Демек, 1), 2) нүктелерінде -дағы функциясының глобәлдік минимумы табылады екен.

5. Енді (1) - (2) есебін

жағдайында қарастырайық.Мәселен (1) - (2) есебі ерекшеленбеген және 1 - 3 алгоритмі бойынша нүктелері анықталған делік.

шектеулерінің ішіндегі болатындарын екшеп алайық, мұндағы индекстер жиыны

. Егер (1) - (2) есебі ерекшеленбеген болса, онда векторлары сызықты тәуелсіз. Жоғарыда келтірілген

теорема бойынша 4 баптан көретініміз: егер квадраттық форма гипержазықтықта оң анықталса, яғни ; онда нүктесі функциясының U -дағы локәлдік минимум нүктесі болады.

ТҮЙІНДЕСТІК ТЕОРИЯСЫ

Бұл лекцияда Лагранж функциясының негізінде негізгі және түйіндес есеп қисындалып, олардың шешімдерінің арасындағы байланыс тағайындалған. Сызықты программалау есебінің негізгі, жалпы және канондық түрлері үшін түйіндес есептер анықталған. Түйіндес есеп дөнес программалау есебі болғандықтан, негізгі есептің дөңес программалау есебі болу-болмауына қарамастан, көпшілік жағдайда түйіндес есепті зерттеп, олардың шешімдері арасындағы байланысты пайдаланып бастапқы есепке оралған жөн. Мұндай тәсіл сызықты программалау есебін шығару кезінде жиі қолданылады. Сызықсыз программалаудың келесі ерекшеленбеген есебін қарастырайық

, (1)

, (2)

Осы (1) - (2) есебі үшін Лагранж функциясын жазамыз:

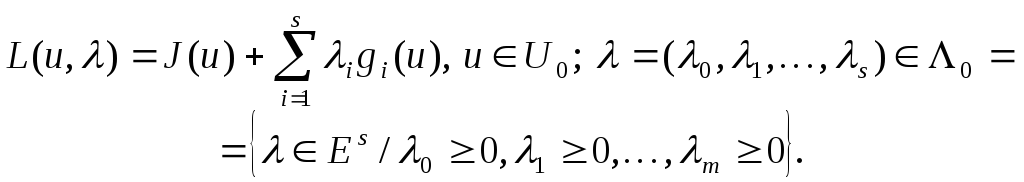(3)

Негізгі есеп. Мына

(4)

функциясын енгізейік. Осы функцияның

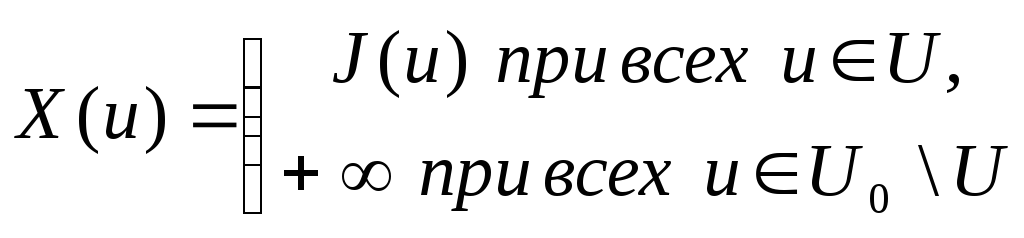(5)

екенін көрсетейік. Шынында да, егер ,онда

;

демек,

себебі барлық кезінде , әрі .

Егер , онда қандай да бір , нөмірі үшін болуы және қандай да бір үшін болуы мүмкін. Екі жағдайда да жеткілікті үлкен немесе тандау арқылы (жеткілікті үлкен сан) мәнін мейлінше үлкен санға жеткізуге болады.

Енді (1) - (2) бастапқы есебін (4) - (5) шартына орай

(6)

түрінде жазуға болады. Байқайтынымыз: демек, егер , онда

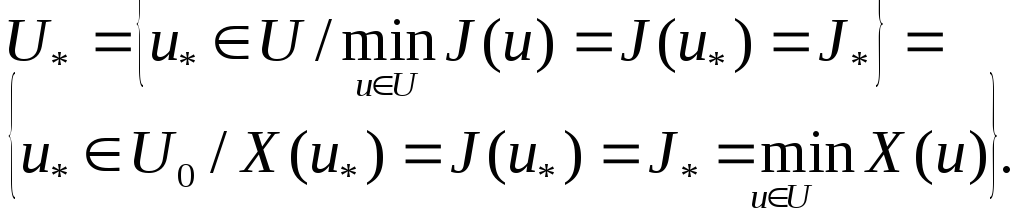
Бастапқы (1) - (2) есебін немесе оған тендес (6) есебін негізгі есеп дейді.

Түйіндес есеп. Лагранж функциясы (3) негізінде

. (7)

функциясын енгіземіз. Мына түрдегі

, (8)

тиімділік есебін (1) - (2) есебіне немесе оған теңдес (6) есебіне түйіндес есеп дейміз, ал Лагранж көбейткіштері - айнымалыларына қарағанда түйіндес айнымалылар деп аталады. Белгілеу:

. Егер , онда .

Лемма. Негізгі (6) және түйіндес (8) есептері үшін шамалары тиісінше келесі шарттарды қанағаттандырады:

(9)

Дәлелі. (7) формуладан көретініміз. Осыдан (4) өрнекке орай

. (10)

Соңғы (10) өрнектен бойынша төменгі мәнге көшсек: .Бұдан және төменгі мән анықтамасынан (9)-теңсіздік алынады. Лемма дәлелденді.

1-ТЕОРЕМА. Мына

, (11)

өрнектері орындалуы үшін Лагранж функциясы (3) жиынында қайқы нүктеге ие болуы қажетті және жеткілікті. функциясының жиынындағы қайқы нүктелерінің жиыны жиынымен беттеседі.

Дәлелі. Қажеттілігі. Мәселен нүктелері үшін (11) өрнегі орындалсын делік. жұбы (3) - Лагранж функциясының жиынындағы қайқы нүктесі екенін көрсетейік.

Болғандықтан (11) өрнегінен алатынымыз

(12)

Осы (12) теңсіздігінен шығатыны

. (13)

Бұл жұбының қайқы нүкте екендігін білдіреді.

Мұның сыртында жиыны Лагранж функциясының нүктелерінің жиынында жатады, өйткені -тиісінше жиынынан алынған нүктелер. Қажеттілік дәлелденді.

Жеткіліктілігі. - жұбы Лагранж функциясының қайқы нүктесі делік. Сонда (11) - өрнек орындалатынын көрсетейік.

Қайқы нүкте анықтамасынан ((13) түріндегі) :

Демек

. (14)

Дәл осылайша, (13) теңсіздігінің сол жағынан:

(15)

Алынған (14), (15) теңсіздіктерінен (9) өрнегін ескере отырып алатынымыз .

Осыдан .Демек, , және мұның сыртында (3) функциясының қайкзы нүктелерінің жиыны жиынында жатады. Теорема дәлелденді.

Лемма мен 1-теоремадан мынадай қорытынды шығаруға болады:

1. Келесі төрт тұжырым өзара мағыналас:

а) - (3) - Лагранж функциясының жиынындағы қайқы нүктесі;

б) (11) өрнектері орындалады;

в) болатын , нүктелері табылады;

г) мына теңсіздік орындалады .

2. Егер нүктелері (3) Лагранж функциясының

-дағы қайқы нүктелері болса, онда нүктелері де (3) функциясының -дағы қайқы нүктелері болып,

Дегенмен, жалпы жағдайда кері тұжырым дұрыс емес, яғни өрнегінен қайқы нүкте екендігі шықпайды.

3. Енді (8) түйіндес есебін

(16)

түрінде жазуға болады. функциясы дөңес жиынында бойынша сызықты болғандықтан, тшмділік есебі (16) дөңес программалау есебіне жатады, негізгі (1) - (2) есебі дөңес пе жоқ па оған қарамастан де дөңес болады. Жалпы жағдайда түйіндес есепке түйіндес есеп бастапқы есеппен беттеспейтінін, яғни, негізгі есепке сай келмейтіндігін байқаймыз. Мұндай сәйкестік тек қана сызықты программалау есебі үшін ғана орын алады.

Түйіндестік теориясының қолданымы ретінде сызықты программалау есебін қарастрайық:

(17)

мұндағы - берілген векторлар, А – берілген ретті матрица,