60. Сызықты емес программалау есебін шешу алгоритмі

Сызықсыз программалау есебі үшін дөңес программалаудағы сияқты Лагранж функциясының қайқы нүктесінің болатындығына кепілдік беретін теоремалар жоқ. Егер қандай да бір жолмен жұбының Лагранж функциясының қайқы нүктесі екендігі тағайындалса, онда нүктесі сызықсыз программалау есебінде де глобәлдік минимум нүктесі екендігі негізгі теоремадан шығады. Төменде сызықсыз программалау есебі үшін Лагранждың жалпыланған функциясының көмегімен тиімділіктің қажетті шарты тұжырымдалған. Ескерту: тиімділік шартынан анықталған , нүктесі жалпы жағдайда есептің шешімі емес, тек "сезікті" нүкте ғана. Шешім алу үшін қосымша зерттеулер қажет. Ең болмаса нүктесі -дағы функциясының локәлдік минимум нүктесі бола ма деген сұраққа жауап беруіміз керек.

ЕСЕПТІҢ ҚОЙЫЛУЫ. ТИІМДІЛІКТІҢ ҚАЖЕТТІ ШАРТЫ

Есептің қойылуы. Практикада келесі есеп жиі кездеседі:

, (1)

, (2)

мұндағы -дегі дөңес жиынында анықталған

дөңес функциялар. Белгілеу енгізейік

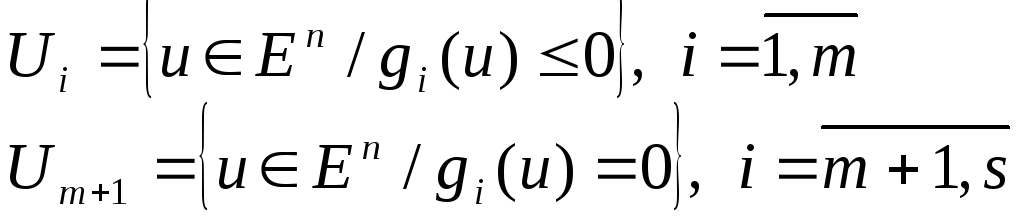(3)

Енді U жиынын мына түрде жаза аламыз

(4)

Сонда (1)-(2) есеп төмендегіше жазылады: .Мәселен

,

делік. Егер , онда екенін байқаймыз. Енді нүктесін және шамасын табу керек.

Лагранждың жалпыланған функциясы (1) - (2) есебі үшін

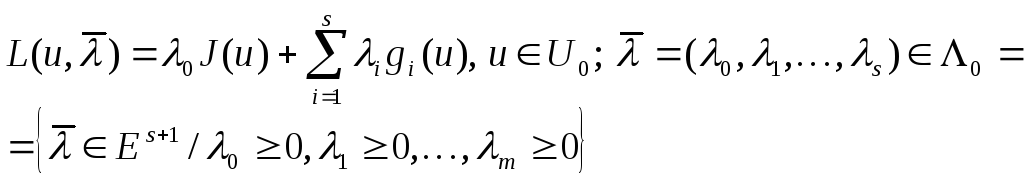(5)

түрінде өрнектеледі.

Айталық дегеніміз жиынын қамтитын ашық жиын болсын.

1-теорема. (Тиімділіктің қажетгі шарты). Егер -дөңес жиын, ал , ондаәрбір нүктесі үшін

, (6)

(7)

(8)

шарттары орындалатын Лагранж көбейткіштері табылуы қажетті.

Дәлелдеуді кейінірек келтіреміз, әуелі 1-теорема шарттарына қысқаша түсінік бере кетейік:

а) дөңес программалау есептеріндегі теоремалардан мұндағы айырмашылық жұбы Лагранж функциясының қайқы нүктесі деп кесіп айтылмайды, яғни негізгі теорема шарты орындалып тұрған жоқ

б) жалпы жағдайда жұбы қайқы нүкте болғандықтан (6)-(8) шарттарынан нүктесі (1) - (2) есебінің шешімі дегеи тұжырым шықпайды.

в) егер , онда (1) - (2) есебі ерекшеленбеген деп аталады, бұл жағдайда деп қабылдауға болады, себебі Лагранж функциясь: -ға қатысты сызықты функция.

г) егер , онда (1) - (2) есебі ерекшеленген деп аталады. Нормалау шартын енгізу арқылы (1) - (2) есебі ерекшеоенген немесе ерекшеленбеген екендігіне байланыссыз, Лагранж көбейткіштерінің, белгісіз санын бірге кемітуге болады яғни (6), шартты мынаған алмастырамыз:

, (9)

мұндағы кез келген сан, дербес жағдайда .

1 мысал. .Берілген есеп үшін жалпыланған Лагранж функциясы:

;

Ал ,Әрі. Онда (7) шарт түрінде жазылады. Осыдан алатынымыз немесе Ал кезінде болғандықтан берілген теңсіздік орындалуы үшін болуы қажет, себебі (6) шарт бойынша . Сонымен бастапқы есеп ерекшеленген есеп екен. Кез келген үшін (8) шарт орындалады. Яғни нүктесінде 1-теореманың барлық шарттары орындалады. Ескерту: берілген есеп үшін әдеттегі Лагранж функциясы қайқы нүктеге ие болмайды.

2 мысал. Мәселен . Сонда . Лагранждың жалпыланған функциясы . болғандықтан (7) шарт түрінде жазылады. Осыдан шығатыны . Демек, Ал (9) шарты деп алуымызға болатыңдығын көрсетеді, мұндағы .Ендеше (8) шарттан . Сонымен тиімділіктің қажетті шарттары (6)-(8) мына нүктелерінде орындалады. Мына тізбегіндегі қандай нүктелерде функциясыжиынындағы минимумына жететіндігін анықтау үшін қосымша зерттеулер жүргізу қажет. нүктелерінде (мұндағы ,)дағы минимуміне жететіндігін аңғару қиын емес.

1-теореманың дәлелдеу үшін мына конустарды құру керек: - функциясының нүктесіндегі кему бағыты, жиындарының нүктесіндегі ішкі бағыттары, нуктесіндегі жиындарының жанама бағыттары.

Конустар құру. нүктесіндегі , конустарын анықтайық.

1 анықтама. Егер барлық үшін

(10)

теңсіздігі орындалатын сандары табылса, онда векторы нүктесіндегі функциясының кему бағыты делінеді . нүктесіндегі функциясының барлық кему бағыттарының жиынын арқылы белгілейміз. Сонымен

. (11)

Осы өрнектегі жиыны е нүктесін және оның аймағын бірге қамтиды, демек - ашық жиын. . , ендеше (қараңыз (10), ).

.

Ашық жиыны нүктесінің аймағын қамтитынын көреміз. Осыдан -ға бөліп және ұмтылдырып, алатынымыз .

Демек:

(12)

жиыны ашық дөңес конус. Фаркаш теоремасы бойынша (12) конусына түйіндес конус

. (13)

формуласынан анықталады.

2 анықтама. Егер барлық үшін тиістіліп орындалатын сандары табылса векторынүктесіндегі жиындарының ішкі бағыттары деп аталады. нүктесіндегі жиыныныц барлық ішкі бағыттарының жиынын арқылы белгілейміз Сонымен

. (14)

- ашық жиын екенін, болатындығын байқаймыз. (1) - (2) есебі үшін жиыны (3)- формуладан анықталады, яғни

.

Онда (4) формуладан анықталатын - жиыны

. (15)

түрінде жазылады.

, ендеше екі жағдай кездеседі: 1) ; 2) . Бірінші жағдайды қарастырайық Бұл кезде функциясы жиынында үзіліссіз болғандықтан барлық мен кез келген векторы үшін болатын саны табылады Ендеше - жиыны ашық конус, ал оған түйіндес конус .

Екінші жағдайда алатынымыз (қараңыз (15)).

Осыдан екенін ескеріп, алатынымыз

. Соңғы өрнекті -ға бөліп,ұмтылдырамыз да нәтижесін жазамыз. Онда ашық, жиыны

(16)

формуласы анықталады. Фаркаш теоремасы бойынша (16) конусына түйіндес конус былай жазылады:

(17)

, ашық дөңес конустар екенін байқаймыз.

3 анықтама. Егер үшін кезде және үшінұмтылатынсаны менфункциясы табылса, ондавекторынүктесіндегіжиынына жанама бағыт деп аталады.нүктесіндегіжиынының барлық жанама бағыттарының жиынынарқылы белгілейміз. Осы анықтамадан шығатыны

демек

, (18)

мұндағы вектор функциясының қасиеті:кезде

. ;ендеше

Осыдан, ға бөліп жәнеұмтылдырған соңкезіндеескеріп, алатынымыз.

Демек, (18) жиыны

. (19)

тұйық дөңес конус. (19) конусына түйіндес конус Фаркаш теоремасы бойынша

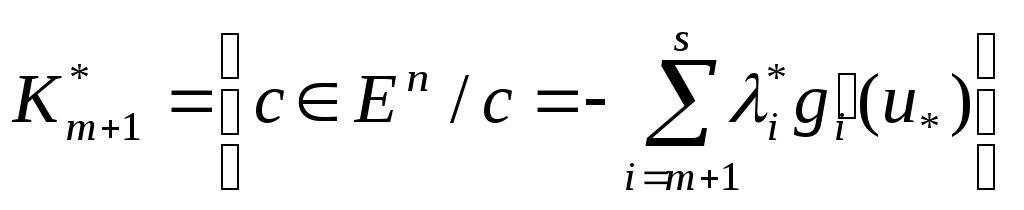. (20)

формуласынан анықталады.

Ақырында, нүктесіндегі дөңесжиынының ішкі бағыттарының жиынынанықтайық. Егер, онда, демекекенін ұғу қиын емес. Егер, онда

(21)

ашық дөңес конус, ал оған түйіндес конус

барлық үшін (22)

Уақыттың тарлығынан конустарды құру қатаң дәлелдеусіз баяндалды.

Бұл айғақтардың дәлелдеулерімен толық баяндалуын оқырман Ф.П.Васильевтің "Численные методы решения экстремальных задач" (М,: Наука, 1980) кітабынан табады.

Бұдан әрі конустарын былай белгілейміз:

Лемма. Егер функциясыныңU жиынындағы минимум нүктесі болса, онда дөңес конустардың қиылысы

. (23)

болуы қажетті.

Дәлелі. делік те (23) өрнек орындалатынын көрсетейік. Қарсы жоримыз: . Онда тиістілігінен шығатыны барлық кезінде. . Алөрнектерінен алатынымыз барлықорындалған шақтарда. Мәселенсандар делік. Ондатеңсіздігі орындалады да, барлық,кезінде. Және, ендеше барлықжәнекезіндегіүшін. Ендівекторын таңдайық:.

Егер және жеткілікті аз сан болса, онда норма .Ендеше

Сонымен, , . Бұл мүмкін емес, себебі нүктесі (1)-(2) есебінің шешімі. Қайшылық лемманы дәлелдейді.

Теореманың дәлелдеуіне көшпес бұрын мыналарды ескерте кетейік:

1) Егер онда кезінде 1-теореманын барлық шарты орындалады. Шынында да норма . скалярлық көбейтінді

2) Егер қандай да бір , үшін , мәндері үшін де онда 1-теорема шарттары орындалады. Шынында да

3) Ақырында, егер векторлары сызықты тәуелді болса, онда да 1-теореманың (6)-(8) шарттары орындалады. Шынында да бұл жағдайда болатын барлығы бірдей нөлге тең емес сандары табылады. десек, норма

себебі .

Осы (1)-(3) баптардан шығатын қорытынды: 1-теореманы, барлық кезінде ,жәневекторлары сызықты тәуелсіз болған жағдайлар үшін дәлелдеген жөн.

1-теореманың дәлелі. Теорема шарты бойынша Онда дәлелденген лемма бойынша нүктесіндегі дөңес конустардың қиылысуы бос жиын:

(24)

әрі конусынан басқа барлық конустар ашық. Байқайтынымыз: ,; -сызықты тәуелсіз жагдайында барлық конустар бос емес (қараңыз (12), (16), (19), (21)). Ендеше (24) өрнегі орындалуы үшін Дубовицкий-Милютин теоремасына сай

. (25)

орындалатын барлығы бірдей нелге тең емес векторларының табылуы қажетті және жеткілікті. (13), (17), (20) формулаларынан:

.

(25)-теңдіктен алатыныныз .