
- •57. Тегіс функциялардың дөңестігінің критерийлері
- •58. Лагранж функциясы. Қайқы нүкте. Негізгі теорема
- •59. Кун-таккер теоремасы.
- •60. Сызықты емес программалау есебін шешу алгоритмі
- •Енді конусы (22) - формуладан анықталғандықтан
- •Лагранж функциясының (17) -есеп үшін жазылған түрі
- •61.Сызықты программалау есебін шешу. Симплекс әдісі
- •2 Мысал. Мәселен
- •Симплекс кесте
- •62. Градиенттік әдіс
- •63. Вариациялық есептеу. Әлді минимум. Әлсіз минимум. Қарапайым есеп.
- •Жалпы жағдайда функционал өсімшесі
- •64. Әлді минимумның қажетті шарттары. Лагранж шарты, якоби шарты, вейерштрасс шарты
- •Функционал мәнін есептейік
- •65. Изопериметрлік есеп. Шартты экстремум
59. Кун-таккер теоремасы.
------------------------------------------------------------------------------------------
Қандай шарттар орындалғанда Лагранж функциясы қайқы нүктеге ие болатындығын тағайындайтын теоремалар Кун-Таккер теоремалары деп аталады (Кун мен Таккер – америкалық математиктер).
Кейде бастапқы
есептің шешімі бар болып (яғни
![]() ,
,![]()
![]()
![]() ),
ал осы есеп үшін Лагранж функциясының
қайқы нүктесі жоқ болуы мүмкін.
),
ал осы есеп үшін Лагранж функциясының
қайқы нүктесі жоқ болуы мүмкін.
Мысал.
![]() ,
ал
,
ал![]() .
.![]() дейік. Әрі
дейік. Әрі![]() және
және![]() функциялары
функциялары![]() жиынындағы дөңес функциялар болсын.U
жиыны жалғыз
элементтен тұрғандықтан, яғни U
={l},
онда
жиынындағы дөңес функциялар болсын.U
жиыны жалғыз
элементтен тұрғандықтан, яғни U
={l},
онда
![]() ={1}.
Демек
={1}.
Демек![]() ,
Лагранж функциясыL
,
Лагранж функциясыL![]() берілген есеп үшін қайқы нүктеге ие
болмайды. Шынында да алдыңғы лекциядағы
(4) формуласынанL
берілген есеп үшін қайқы нүктеге ие
болмайды. Шынында да алдыңғы лекциядағы
(4) формуласынанL![]() L
L![]() .
Осыдан алатынымыз
.
Осыдан алатынымыз
![]() ,
мұндағы
,
мұндағы![]() .
Жеткілікті аз
.
Жеткілікті аз![]() кезінде берілген теңсіздік орындалатын
кезінде берілген теңсіздік орындалатын![]() саны табылмайды. Төмендегі жағдайларға
тоқталайық.
саны табылмайды. Төмендегі жағдайларға
тоқталайық.
1-жағдай. Дөңес программалаудың келесі есебін қарастырайық
![]() (1)
(1)
![]() (2)
(2)
мұндағы
![]() -
-![]() жиынында анықталған дөңес функциялар.
жиынында анықталған дөңес функциялар.
1 анықтама.
Егер
![]() болатын
болатын![]() нүктесі табылса, онда
нүктесі табылса, онда![]() шектеуі
шектеуі![]() жиынындарегуляр
делінеді.
Егер барлық (2) шартындағы
жиынындарегуляр
делінеді.
Егер барлық (2) шартындағы
![]() шарттары
шарттары![]() жиынындарегуляр
болса,онда
U
регуляр
жиын
деп аталады.
жиынындарегуляр
болса,онда
U
регуляр
жиын
деп аталады.
Мәселен
![]() (3)
(3)
орындалатын
![]() нүктесі бар болсын. Осы (3) шартыСлейтер
шарты деп
аталады.
нүктесі бар болсын. Осы (3) шартыСлейтер
шарты деп
аталады.
Мәселен
![]() нүктелерінде барлық шектеулер
регуляр,
яғни
нүктелерінде барлық шектеулер
регуляр,
яғни
![]() болсын. Онда
болсын. Онда
![]() нүктесінде
нүктесінде
![]() барлық
барлық![]() шектеулері
регуляр.
Шынында да,
шектеулері
регуляр.
Шынында да,
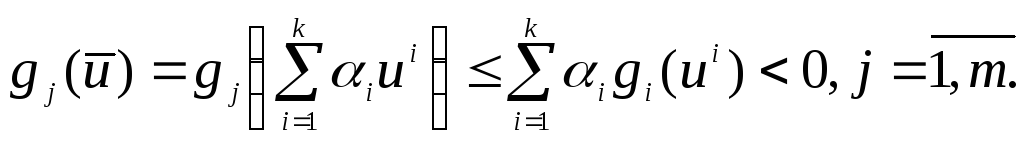
1 теорема.
Егер
![]() - дөңес
- дөңес![]() жиынында анықталған функциялар,U
жиыны
регуляр
және
жиынында анықталған функциялар,U
жиыны
регуляр
және
![]() , онда әрбір
, онда әрбір![]() нүктесі үшін
нүктесі үшін![]() жұбы Лагранж функциясының:L
жұбы Лагранж функциясының:L![]() қайқы нүктесін
құратын Лагранж көбейткіштері
қайқы нүктесін
құратын Лагранж көбейткіштері
![]() табылуы қажетті. Теорема шартынан
байқайтынымыз: дөңес программалау есебі
(1), (2) үшін егерU
жиыны
регуляр
болса (
табылуы қажетті. Теорема шартынан
байқайтынымыз: дөңес программалау есебі
(1), (2) үшін егерU
жиыны
регуляр
болса (![]() шарты орындалғанда) Лагранж функциясы
қайқы нүктеге ие болады екен.
шарты орындалғанда) Лагранж функциясы
қайқы нүктеге ие болады екен.
Ескерту:
Жоғарыда келтірілген мысалда U
жиыны
регуляр
емес, өйткені жалғыз
![]() нүктесінде шектеу
нүктесінде шектеу![]() .
Байқайтынымыз: егер жиынрегуляр
болса, онда Слейтер шарты бойынша
.
Байқайтынымыз: егер жиынрегуляр
болса, онда Слейтер шарты бойынша
![]() .
.
Дөңес программалау
есептері үшін, Лагранж функциясы қайқы
нүктеге ие болатын, U
жиынына
қойылатын қосымша шарттар алынды. Ақырлы
өлшемді кеңістікте тиімділік есебін
Лагранж көбейткіштері әдісімен шешу
үшін
![]() шартының сыртында Лагранж функциясының
қайқы нүктесі табылуы қажеттігін еске
сала кетейік. Тек осы жағдайда ғана
негізгі теореманы қолданған орынды.
шартының сыртында Лагранж функциясының
қайқы нүктесі табылуы қажеттігін еске
сала кетейік. Тек осы жағдайда ғана
негізгі теореманы қолданған орынды.
1 теореманың
дәлелі
![]() кеңістігіндегі А мен В жиындарының
ажырамалылығы туралы теорема негізінде
жүргізіледі. А мен В жиындары келесі
түрде анықталсын
кеңістігіндегі А мен В жиындарының
ажырамалылығы туралы теорема негізінде
жүргізіледі. А мен В жиындары келесі
түрде анықталсын
![]() (4)
(4)
![]() (5)
(5)
мұндағы
![]() ,
себебі
,
себебі![]() .
Енді мыналарды көрсетейік:
.
Енді мыналарды көрсетейік:
а) А мен В
жиындарының ортақ нүктесі жоқ. Шынында
да
![]() ,
тиістілігінен шығатыны
,
тиістілігінен шығатыны![]() .
Егер
.
Егер![]() ,
онда
,
онда![]() теңсіздігі орындалады, демек
теңсіздігі орындалады, демек![]() .
Егер
.
Егер![]() ,
онда қандай да бір
,
онда қандай да бір![]() нөмірі үшін
нөмірі үшін![]() .
Ендеше
.
Ендеше![]() және тағы да
және тағы да![]() .
Сонымен
.
Сонымен![]() .
.
б) А мен В - дөңес
жиындар. Еркін екі
![]() нүктелері мен
нүктелері мен![]() санын алайық.
санын алайық.![]() тиістілігінен
тиістілігінен![]() болатын
болатын![]() нүктесі табылатындығын көреміз. Дәл
осылайша,
нүктесі табылатындығын көреміз. Дәл
осылайша,![]() екендігінен алатынымыз
екендігінен алатынымыз![]() ,
мұндағы
,
мұндағы![]() .
Сонда
.
Сонда![]() ,
әрі
,
әрі![]() да
да![]() дөңес болған соң
дөңес болған соң![]() мұндағы
мұндағы![]() .
Дәл осылай
.
Дәл осылай![]() жиынында
жиынында![]() функциялары дөңес болғандықтан
функциялары дөңес болғандықтан![]() .
Сонымен
.
Сонымен![]() әрі
әрі![]() .
Осыдан
.
Осыдан![]() кезінде
кезінде![]() екендігі шығады. Демек, А жиыны дөңес
екен. В жиынының да дөңестігі осы жолмен
дәлелденеді.
екендігі шығады. Демек, А жиыны дөңес
екен. В жиынының да дөңестігі осы жолмен
дәлелденеді.
в) А мен В
жиындары дөңес және
![]() болған соң, 2-теоремаға (6-дәріс) сай А
мен В жиындарын , сонымен қатар олардың
тұйықтамасын да ажырататын
болған соң, 2-теоремаға (6-дәріс) сай А
мен В жиындарын , сонымен қатар олардың
тұйықтамасын да ажырататын![]() гипержазықтығы
табылады (мұндағы нормәл вектор
гипержазықтығы
табылады (мұндағы нормәл вектор![]() ).
Демек
).
Демек
![]() (6)
(6)
шарты орындалады.
Егер
![]() , онда
, онда![]() ,
демек
,
демек![]() және
және![]() екендігін байқаймыз.
екендігін байқаймыз.
Еңді (6) теңсіздігі
![]() (7)
(7)
түрінде жазылады.
Осыдан, дербес жағдайда
![]() кезіндегі сол жақтағы теңсіздіктен
алатынымыз
кезіндегі сол жақтағы теңсіздіктен
алатынымыз![]() .
Демек,
.
Демек,![]() Дәл осылайша
Дәл осылайша![]() векторын
векторын![]() түрінде таңдап, сол жақтағы теңсіздіктен
алатынымыз
түрінде таңдап, сол жақтағы теңсіздіктен
алатынымыз![]() .Осыдан
.Осыдан![]() .
.
г) Кез келген
![]() нүктесін алайық.
нүктесін алайық.![]() екендігін байқау қиын емес, себебі
екендігін байқау қиын емес, себебі![]() .
Осы нүктені (7) теңсіздігінің оң және
сол жақтарына қойсақ:
.
Осы нүктені (7) теңсіздігінің оң және
сол жақтарына қойсақ:![]() .
Осыдан алатынымыз
.
Осыдан алатынымыз![]() ,
демек
,
демек![]()
д)
![]() .
Жоғарыдағы в) бабында
.
Жоғарыдағы в) бабында![]() екенін көрсеттік. Теорема шарты бойыншаU
жиыны регуляр.
Яғни Слейтер шарты (3) орындалады. Демек,
екенін көрсеттік. Теорема шарты бойыншаU
жиыны регуляр.
Яғни Слейтер шарты (3) орындалады. Демек,
![]() болатын
болатын![]() нүктесі табылады. Байқайтынымыз
нүктесі табылады. Байқайтынымыз![]() .
Ендеше (7) теңсіздігінің оң жағынан
алатынымыз
.
Ендеше (7) теңсіздігінің оң жағынан
алатынымыз![]() .
.
Қарсы жориық:
![]() .
Вектор
.
Вектор![]() ,
онда
,
онда![]() сандарының кемінде біреуі нөлден ерекше.
Ендеше теңсіздіктен
сандарының кемінде біреуі нөлден ерекше.
Ендеше теңсіздіктен![]() .
Бұл мүмкін емес, себебі
.
Бұл мүмкін емес, себебі![]() .
Сонымен,
.
Сонымен,![]() саны нөлге тең емес, демек,
саны нөлге тең емес, демек,![]() .
Жалпы
.
Жалпы![]() деп алуымызға болады.
деп алуымызға болады.
е)
![]() нүкте болсын. Онда вектор
нүкте болсын. Онда вектор![]() (7) теңсіздігінің оң жағынан алатынымыз
(7) теңсіздігінің оң жағынан алатынымыз![]() .
Мына көбейтінді
.
Мына көбейтінді![]() ,
онда
,
онда![]() .
.
Осы теңсіздіктен
және
![]() ,
теңдігінен шығатыны
,
теңдігінен шығатыны![]() жұбы Лагранж функциясының қайқы нүктесі,
мұндағы
жұбы Лагранж функциясының қайқы нүктесі,
мұндағы![]() .
Теорема дәлелденді.
.
Теорема дәлелденді.
2-жағдай. Енді дөңес программалаудың келесі есебін қарастырайық:
![]() (8)
(8)
![]() (9)
(9)
мұндағы
![]() - жиынша,
- жиынша,
![]() жиын,
жиын,
![]() -дөңес
-дөңес
![]()
жиынында анықталған
дөңес функция,
![]() берілген векторлар,
берілген векторлар,![]() берілген сандар. Осы (8), (9) есебі үшін
Лагранж функциясын жазайық
берілген сандар. Осы (8), (9) есебі үшін
Лагранж функциясын жазайық
L![]()
![]() (10)
(10)
Егер функция
![]() сызықты болса, онда (8)-(9) есебі сызықты
программалаудың жалпы есебі деп аталады.
Мәселен
сызықты болса, онда (8)-(9) есебі сызықты
программалаудың жалпы есебі деп аталады.
Мәселен![]() делік. Жоғарыдағы (8)-(9) есебі үшін жазылған
Лагранж функциясы (10) дөңесU
жиынына қосымша ешқандай шарт
қойылмаса да қайқы нүктеге ие болады
екен. Мұны дәлелдеу үшін келесі лемма
қажет.
делік. Жоғарыдағы (8)-(9) есебі үшін жазылған
Лагранж функциясы (10) дөңесU
жиынына қосымша ешқандай шарт
қойылмаса да қайқы нүктеге ие болады
екен. Мұны дәлелдеу үшін келесі лемма
қажет.
Лемма.
Егер
![]() саны ақырлы векторлар және
саны ақырлы векторлар және![]() ,
,
онда
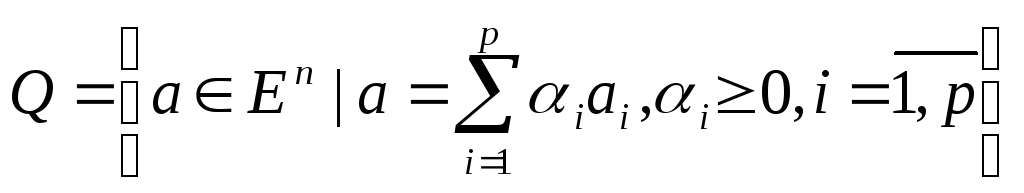 (11)
(11)
жиыны тұйық конус болғаны.
Дәлелдеу.
![]() конус екендігін көрсетейік. Шынында да
, егер
конус екендігін көрсетейік. Шынында да
, егер
![]() және
және
![]() еркін
сан болса, онда
еркін
сан болса, онда
![]() мұндағы
мұндағы
![]()
![]() .
Осыдан шығатыны
.
Осыдан шығатыны
![]() .
Демек жиыны конус. Енді
.
Демек жиыны конус. Енді
![]() дөңес конус екендігін көрсетейік.
Нақтысында,
дөңес конус екендігін көрсетейік.
Нақтысында,
![]() тиістілігінен
шығатыны
тиістілігінен
шығатыны
![]()
![]()
мұндағы
![]() .
Осыдан,
барлық
.
Осыдан,
барлық
![]() кезінде
кезінде
алатынымыз
![]() .
Демек,
.
Демек,
![]() жиыны
дөңес
конус.
жиыны
дөңес
конус.
![]() дөңес
тұйық
конус
екендігін
көрсетейік.
Математикалық
индукция
арқылы
дәлелдейміз.
дөңес
тұйық
конус
екендігін
көрсетейік.
Математикалық
индукция
арқылы
дәлелдейміз.
![]() мәні
үшін
алатынымыз
мәні
үшін
алатынымыз
![]() жарты
түзу.
Яғни
жарты
түзу.
Яғни
![]() -тұйық
жиын.
-тұйық
жиын.
![]()
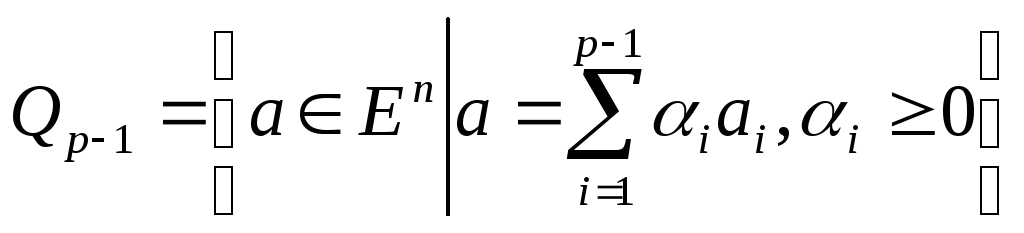 жиыны
тұйық
делік
. Енді
жиыны
тұйық
делік
. Енді
![]() жиынының
тұйықтығын
дәлелдейік.
Мәселен,
жиынының
тұйықтығын
дәлелдейік.
Мәселен,
![]()
![]() жиынының
шекті
нүктесі
болсын.
Демек
жиынының
шекті
нүктесі
болсын.
Демек
![]() тізбегі
табылады,
әрі
тізбегі
табылады,
әрі
![]() .
.
![]() тізбегі
тізбегі
![]() түрінде
өрнектеледі,
мұндағы
түрінде
өрнектеледі,
мұндағы
![]() - сан
тізбегі.
- сан
тізбегі.
![]() жиыны
тұйық
болғандықтан,
жиыны
тұйық
болғандықтан,
![]() әрі
әрі
![]() ,
енді
,
енді
![]() сан
тізбегінің
шектелгендігін
дәлелдесек
болғаны.
Қарсы
жориық
сан
тізбегінің
шектелгендігін
дәлелдесек
болғаны.
Қарсы
жориық
![]() .
.
![]() ,
ал
,
ал
![]() тізбегі
шектелген,
себебі
тізбегі
шектелген,
себебі
![]() , онда
, онда
![]() кезінде
кезінде
![]() .
.
![]() болғандықтан
(
болғандықтан
(![]() жағдайында)
жағдайында)
![]() .
Бұл
мүмкін
емес.
Демек
.
Бұл
мүмкін
емес.
Демек
![]() тізбігі
шектелген.
Яғни
тізбігі
шектелген.
Яғни
![]() ,
мұндағы
,
мұндағы
![]() .
Лемма
дәлелденді.
.
Лемма
дәлелденді.
Енді (8)-(9) есебі үшін жазылған Лагранж функциясының қайқы нүктесі бар болуы туралы теореманы дәлелдемес бұрын дөңестік анализі теориясында маңызды орын алатын Фаркаш теоремасын тұжырымдап, және оны дәлелдейік.
Фаркаш теоремасы. Егер төбесі нөлдегі конусы
![]() (12)
(12)
теңсіздіктерімен анықталса, онда оған түйіндес конус мына түрде жазылады:
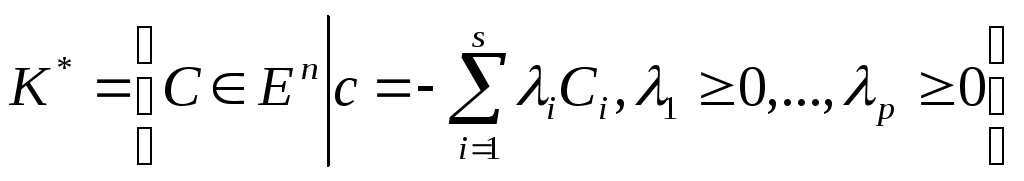 (13)
(13)
Дәлелі.
К
конусы (12) формуласымен анықталсын.
![]() болатын
болатын![]() векторларының жиыны (13) формуласынан
анықталатындығын , яғни
векторларының жиыны (13) формуласынан
анықталатындығын , яғни
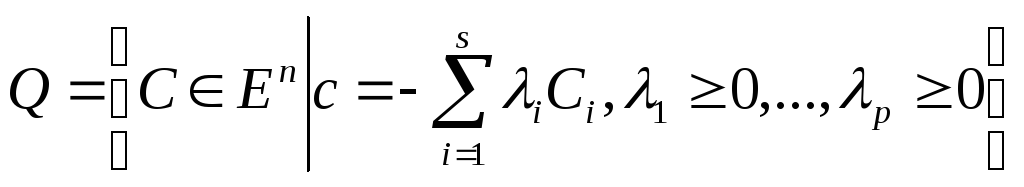 (14)
(14)
жиыны
![]() жиынмен беттесетіндігін көрсетейік.
жиынмен беттесетіндігін көрсетейік.![]() болсын.
Онда (14) - тегі
болсын.
Онда (14) - тегі
![]() жиыны
жиыны
 (15)
(15)
түрінде жазылады.
Осы (15) пен (11) өрнектерінен көретініміз:
![]() векторларынан туындаған
векторларынан туындаған
![]() тұйық конус (лемманы қараңыз).
тұйық конус (лемманы қараңыз).
![]() екенін көрсетейік.
Шындығында да, егер
екенін көрсетейік.
Шындығында да, егер
![]() яғни
яғни![]() ,
онда (12) өрнегінің арқасында
,
онда (12) өрнегінің арқасында![]() .
Демек,
.
Демек,![]() векторы
векторы![]() жиынында жатады. Осыдан шығатыны
жиынында жатады. Осыдан шығатыны![]() .
.
![]() екенін көрсетейік.
Қарсы жоримыз:
екенін көрсетейік.
Қарсы жоримыз:
![]() ,
бірақ
,
бірақ![]() .
.
![]() жиыны тұйық дөңес конус және
жиыны тұйық дөңес конус және
![]() ,
ендеше 1-теоремаға сай (6-лекция)
,
ендеше 1-теоремаға сай (6-лекция)![]() нүктесі
нүктесі
![]() жиынынан әлді ажырайды, яғни
жиынынан әлді ажырайды, яғни
![]() ,
мұндағы
,
мұндағы![]() гипержазықтығына нормәл вектор. Осыдан
алатынымыз
гипержазықтығына нормәл вектор. Осыдан
алатынымыз
![]() (16)
(16)
![]() векторын төмендегіше
таңдаймыз:
векторын төмендегіше
таңдаймыз:
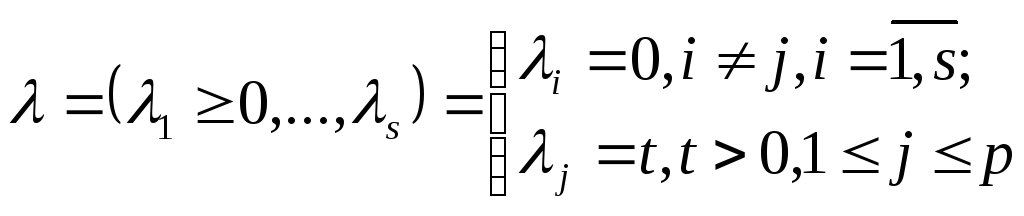
Осы
![]() векторы үшін , (27) теңсіздігі
векторы үшін , (27) теңсіздігі![]() түрінде жазылады. Оны
түрінде жазылады. Оны![]() бөліп және
бөліп және![]() ұмтылдырып, нәтижесінде алатынымыз
ұмтылдырып, нәтижесінде алатынымыз![]() Бұдан әрі
Бұдан әрі
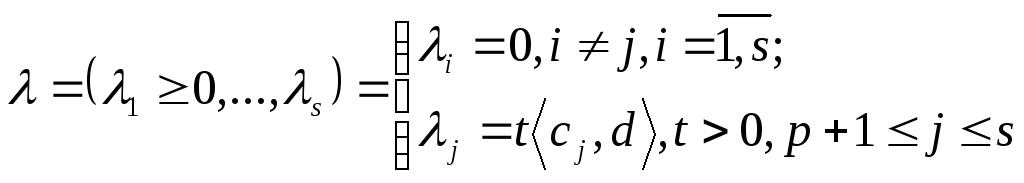
векторын аламыз.
(16) - теңсіздіктен
![]() .Оны
.Оны![]() бөліп және
бөліп және![]() ұмтылдырып алатынымыз
ұмтылдырып алатынымыз![]() .
.
Сонымен
![]() векторы үшін
векторы үшін![]() ;
;![]() .
Онда (12)-ден шығатыны
.
Онда (12)-ден шығатыны![]() ,
,![]() –
–![]() мұндағы жиынының тұйықталуы.
мұндағы жиынының тұйықталуы.
Вектор
![]() болғандықтан
болғандықтан![]() теңсіздігі орындалады Осыдан, дербес
жағдайда,
теңсіздігі орындалады Осыдан, дербес
жағдайда,![]() үшін
үшін![]() .
Дегенмен (16)-да
.
Дегенмен (16)-да![]() кезінде алатынымыз
кезінде алатынымыз![]() .
Қайшылыққа ұшырадық.
.
Қайшылыққа ұшырадық.
Демек,
![]() векторы
векторы![]() жиынында жатады.
жиынында жатады.![]() тиістіліктерінен
тиістіліктерінен![]() .
Теорема дәлелденді.
.
Теорема дәлелденді.
Енді дөңес программалаудың (8)-(9) есебі үшін жазылған Лагранж функциясының қайқы нүктесі бар болатындығы туралы теореманы қарастырайық .
2 теорема. Егер
![]() дөңес
дөңес![]() жиынындағы дөңес функция,
жиынындағы дөңес функция,![]() және (8) - (9) есебі үшін
және (8) - (9) есебі үшін![]() болса, онда әрбір
болса, онда әрбір![]() нүктесі үшін
нүктесі үшін![]() жұбы (10) - Лагранж функциясының
жұбы (10) - Лагранж функциясының![]() жиынындағы қайқы нүктесін құратын
Лагранж көбейткіштері
жиынындағы қайқы нүктесін құратын
Лагранж көбейткіштері![]() табылуы қажет.
табылуы қажет.
Дәлелі.
Теореманың барлық шарттары орындалғанда
![]() жұбы (10) - Лагранж функциясының қайқы
нүктесі болатындығын көрсетейік. Мәселен
жұбы (10) - Лагранж функциясының қайқы
нүктесі болатындығын көрсетейік. Мәселен![]() - еркін нүкте. Дөңес
- еркін нүкте. Дөңес![]() жиыны үшін
жиыны үшін![]() нүктесінен шығатын ұйғарымды бағыттарды
анықтайық.
нүктесінен шығатын ұйғарымды бағыттарды
анықтайық.
Ескерту:
Егер барлық
![]() кезінде
кезінде![]() болатын
болатын![]() саны табылса, онда
саны табылса, онда![]() векторы
векторы![]() нүктесінде ұйғарымды бағыт деп аталады.
нүктесінде ұйғарымды бағыт деп аталады.![]() тиістілігінен (9) өрнекті ескере отырып
алатынымыз
тиістілігінен (9) өрнекті ескере отырып
алатынымыз
![]()
![]() (17)
(17)
Егер индекстер
жиынын
![]() енгізсек, онда (17) шарттың жазылуы:
енгізсек, онда (17) шарттың жазылуы:
![]() (18)
(18)
Сонымен, (18) өрнегінен
көретініміз
![]() нүктесіндегі ұйғарымды бағыттар жиыны
конус екен:
нүктесіндегі ұйғарымды бағыттар жиыны
конус екен:
![]() (19)
(19)
мұндағы
![]() бірлік вектор. Кері тұжырым да дұрыс.
Яғни, егер
бірлік вектор. Кері тұжырым да дұрыс.
Яғни, егер![]() ,
онда
,
онда![]() -
ұйғарымды бағыт.
-
ұйғарымды бағыт.
![]() дөңес
дөңес
![]() жиынындағы дөңес функция және
жиынындағы дөңес функция және![]() болғандықтан 4-теоремаға сай
болғандықтан 4-теоремаға сай![]() нүктесінде
нүктесінде![]() теңсіздігінің орындалуы қажет және
жеткілікті. Осыдан
теңсіздігінің орындалуы қажет және
жеткілікті. Осыдан![]() ескеріп, алатынымыз
ескеріп, алатынымыз![]() .
Демек
.
Демек![]() Фаркаш теоремасы бойынша (19) конусына
түйіндес конус
Фаркаш теоремасы бойынша (19) конусына
түйіндес конус![]() (13) формуладан анықталады, сондықтан
(13) формуладан анықталады, сондықтан
![]() (20)
(20)
теңдігі орындалатын
![]() сандары табылады. Мәселен,
сандары табылады. Мәселен,![]() мәндері үшін
мәндері үшін![]() болсын. Онда (19) өрнек
болсын. Онда (19) өрнек
![]() (21)
(21)
түрінде жазылады.
Ескерту:
![]() себебі
себебі![]() өрнектен (10) көретініміз:
өрнектен (10) көретініміз:
![]() (22)
(22)
![]() дөңес функция ,
ендеше 1-теоремаға сай (4-лекция)
дөңес функция ,
ендеше 1-теоремаға сай (4-лекция)
![]() .
Енді (18) теңдікті (21) өрнегін ескере
отырып -
.
Енді (18) теңдікті (21) өрнегін ескере
отырып -
![]()
![]()
түрінде
жазуға
болады.
![]() .
Осыдан
.
Осыдан
![]() .
Осы
теңсіздік
пен
.
Осы
теңсіздік
пен
![]() теңдігінен
теңдігінен
![]() жұбы
(21) - Лагранж
функциясының
қайқы
нүктесі
екендігін
көреміз.
Теорема
дәлелденді.
жұбы
(21) - Лагранж
функциясының
қайқы
нүктесі
екендігін
көреміз.
Теорема
дәлелденді.
3-жағдай. Дөңес программалаудың неғүрлым жалпы есебін қарастырайық
![]() (23)
(23)
![]()
![]() (24)
(24)
мұндағы
![]() дөңес
дөңес
![]() жиынында
анықталған
дөңес
функциялар,
жиынында
анықталған
дөңес
функциялар,
![]() - берілген
векторлар,
- берілген
векторлар,
![]() берілген
сандар.
Осы
(34)-(35) есебі
үшін
Лагранж
функциясы:
берілген
сандар.
Осы
(34)-(35) есебі
үшін
Лагранж
функциясы:
![]() (25)
(25)
3
теорема.
Егер
![]() дөңес
дөңес
![]() жиынындағы
анықталған
дөңес
функциялар;
(34)-(35) есебі
үшін
жиынындағы
анықталған
дөңес
функциялар;
(34)-(35) есебі
үшін
![]() және
және
![]() орындалатын
орындалатын
![]() нүктесі
табылса,
онда
әрбір
нүктесі
табылса,
онда
әрбір
![]() нүктесі
үшін
нүктесі
үшін
![]() жұбы
жұбы
![]() жиынында
(36)-Лагранж
функциясының
қайқы
нүктесін
құратын
Лагранж
көбейткіштері
жиынында
(36)-Лагранж
функциясының
қайқы
нүктесін
құратын
Лагранж
көбейткіштері
![]() табылуы
қажетті.
табылуы
қажетті.
Теореманың дәлелдеуі 1-6 теоремаларға қарағанда (1.4) дөңес жиындардың ажырамалылығы туралы терең мағыналы теоремаларды қолдануды қажет етеді. Сондықтан, мұндай теоремалармен жете танысу үшін Р. Рокафеллердің кітабын ұсынамыз (Выпуклый анализ.-М.: Мир, 1973.).
Ескерте кететін мәселелер:
1. Жоғарыдағы 1-3 теоремалар дөңес программалау есебі үшін қайқы нүкте болуының жеткілікті шарттарын береді.
1-мысал.
Мәселен
![]() ,
ал
,
ал
![]() делік.
Осы
мысалдағы
делік.
Осы
мысалдағы
![]() функциялары
дөңес
функциялары
дөңес
![]() жиынындағы
дөңес
функциялар.
жиынындағы
дөңес
функциялар.
![]() демек
демек
![]() .
.
![]() нүктесі
мен
нүктесі
мен
![]() шамасы
шамасы
![]() есебінің
шешімі
болып
табылады.
Лагранж
функциясы
есебінің
шешімі
болып
табылады.
Лагранж
функциясы
![]() .
.
![]() ,
демек
,
демек
![]() жұбы
Лагранж
функциясының
қайқы
нүктесі.
Берілген
мысал
үшін
1-теоремадағы
Слейтер
шарты
да,
3-теорема
шарты
да
орындалмағандығын
байқаймыз.
жұбы
Лагранж
функциясының
қайқы
нүктесі.
Берілген
мысал
үшін
1-теоремадағы
Слейтер
шарты
да,
3-теорема
шарты
да
орындалмағандығын
байқаймыз.
2. Жалпы
жағдайда
![]() нүктесі
үшін
Лагранж
көбейткіштері
бір
мәнді
анықталмайды.
Келтірілген
мысал
үшін
нүктесі
үшін
Лагранж
көбейткіштері
бір
мәнді
анықталмайды.
Келтірілген
мысал
үшін
![]() жұбы
кез
келген
жұбы
кез
келген
![]() кезінде
Лагранж
функциясының
қайқы
нүктесі
болады.
кезінде
Лагранж
функциясының
қайқы
нүктесі
болады.
3. 1-3 теоремалардың шарттарының орындалуы - Лагранж функциясының қайқы нүктесінің болатындығының кепілі. Айта кететін мәселе - сызықсыз программалау үшін де, дөңес программалау үшін де Лагранж функциясының қайқы нүктесін табу экстремәлді есептер теориясындағы әзірше аз зерттелген мәселе.
Дөңес программалау есебін шығару алгоритмі. Қолданбалы зеттеулерде (23)-(24) түрінде жазылған дөңес программалау есептері жиі ұшырасады. Жоғарыдағы теория негізінде дөңес программалау есебін шығарудың тәртібін қысқаша баяндайық.
(23)-(24) есебі үшін
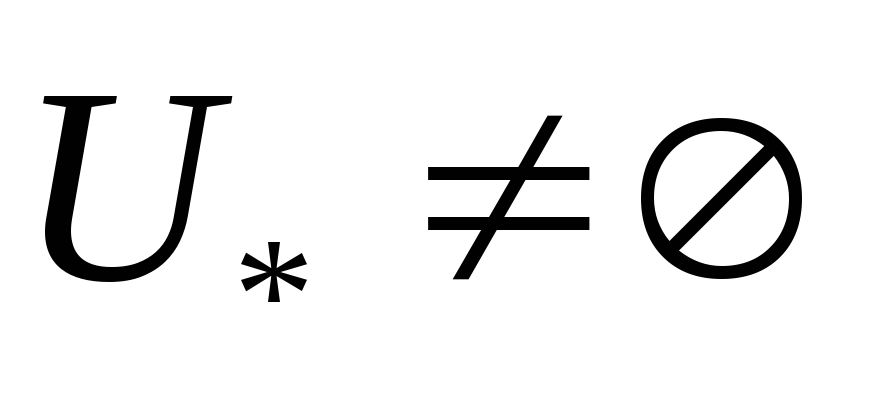 екендігіне көз жеткізу керек. Ол үшін
1-3 теоремаларды (Вейерштрасс теоремаларын)
қолданамыз.
екендігіне көз жеткізу керек. Ол үшін
1-3 теоремаларды (Вейерштрасс теоремаларын)
қолданамыз.Дөңес программалау есебінің түріне байланысты Лагранж функциясының қайқы нүктесінің болатындығына кепілдік беретін шарттардың орындалуын тексереміз (Жоғарыдағы 1-3 теоремалар шарттары). Мысалы, егер есеп (1)-(2 түрінде болса, онда
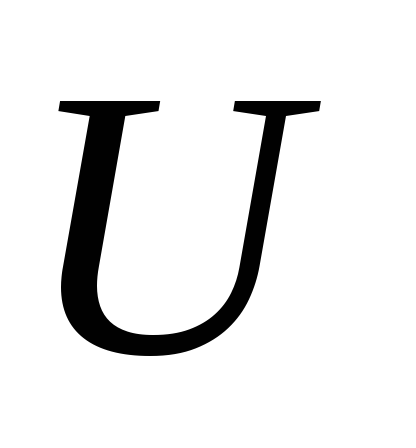 регуляр
екендігін , егер есеп (8)-(9) түрінде болса,
онда
регуляр
екендігін , егер есеп (8)-(9) түрінде болса,
онда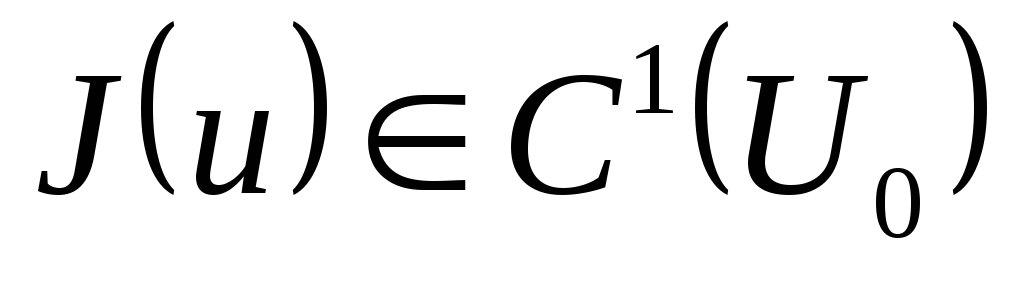 екендігін, ал (23)-(24) есебі үшін
екендігін, ал (23)-(24) есебі үшін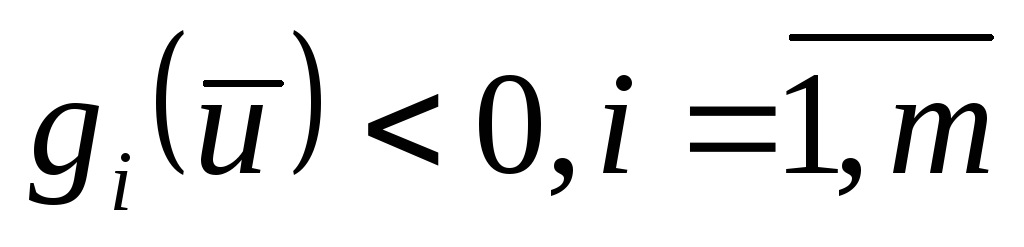 орындалатын
орындалатын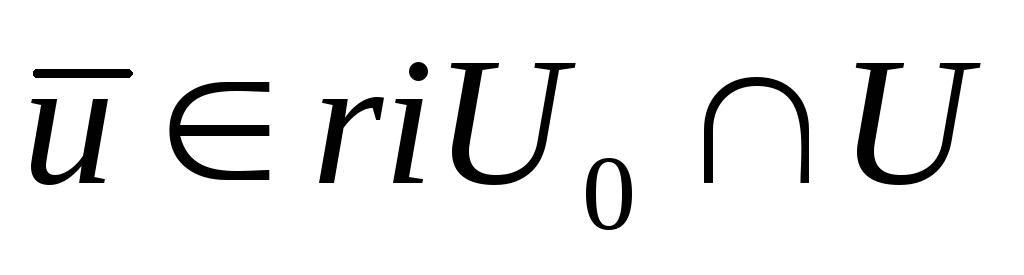 нүктесі табылатындығын көрсетеміз.
нүктесі табылатындығын көрсетеміз.Анықталу аймағы
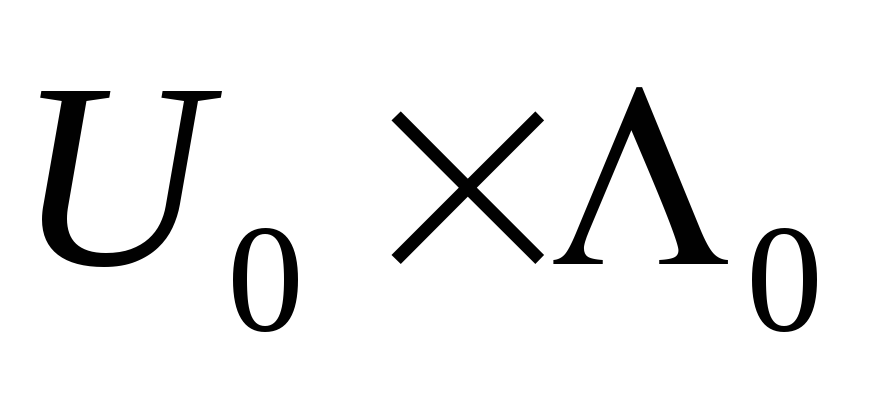 Лагранж
Лагранж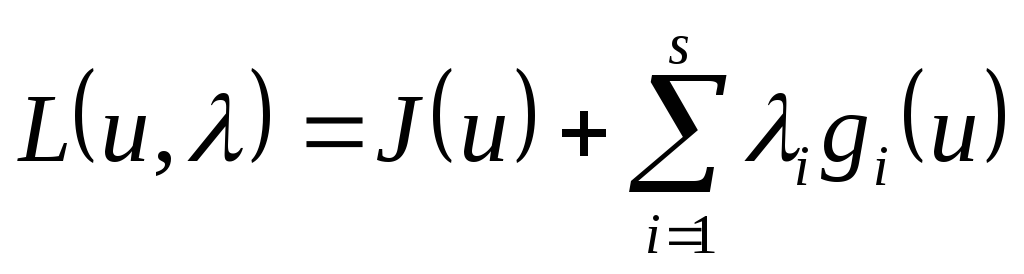 құрамыз, мұндағы
құрамыз, мұндағы .
.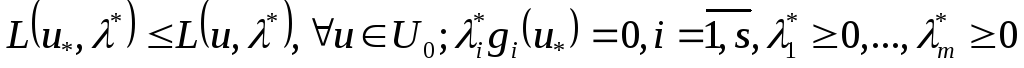 (26)
шартынан (негізгі лемма) Лагранж
функциясының
(26)
шартынан (негізгі лемма) Лагранж
функциясының
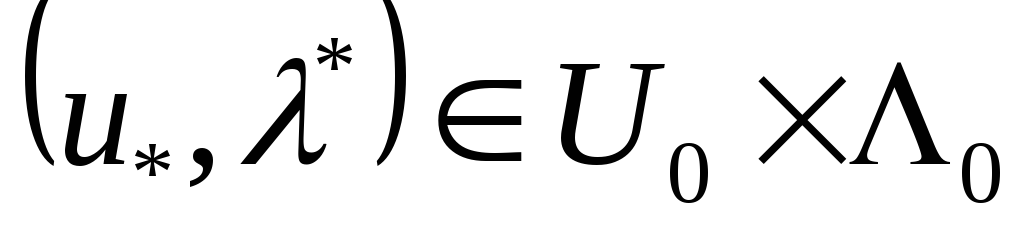 қайқы нүктесін табамыз.
а) Бірінші шарттан
көретініміз
қайқы нүктесін табамыз.
а) Бірінші шарттан
көретініміз функциясы
функциясы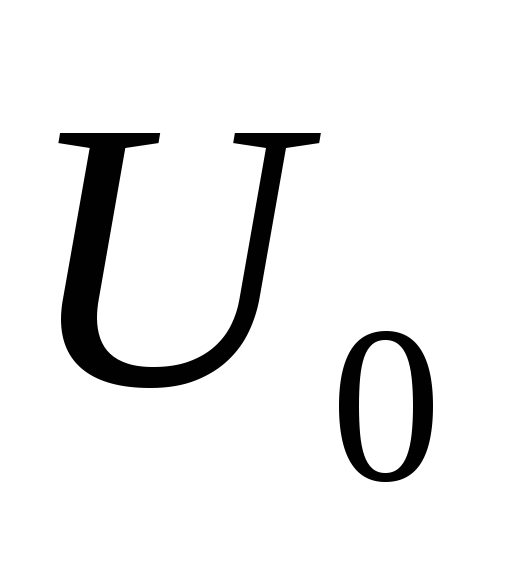 жиынындағы минимумына
жиынындағы минимумына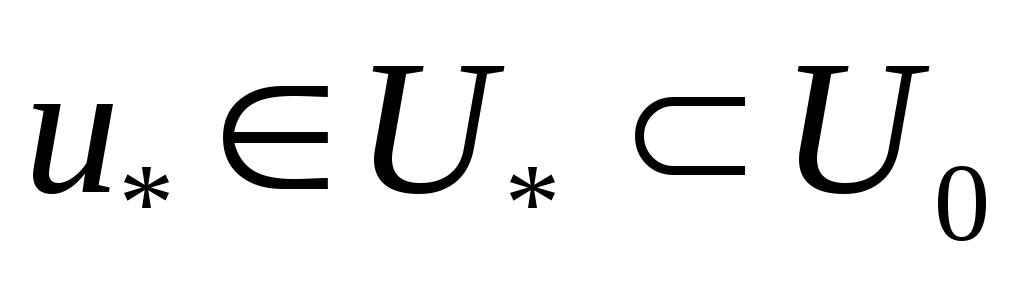 нүктесінде жетеді.
нүктесінде жетеді. функциялары дөңес
функциялары дөңес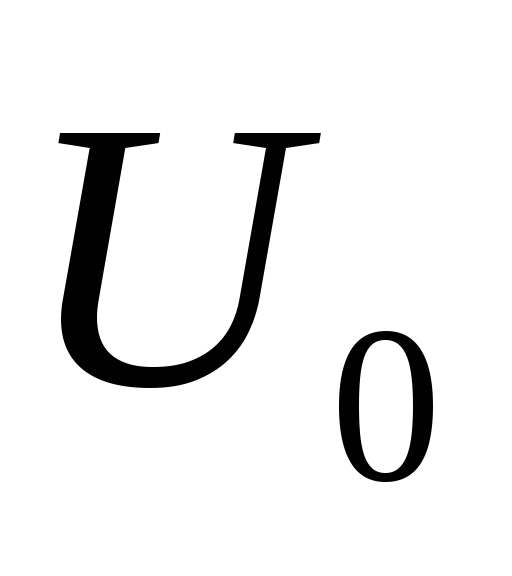 жиынындағы дөңес функциялар, ендеше
жиынындағы дөңес функциялар, ендеше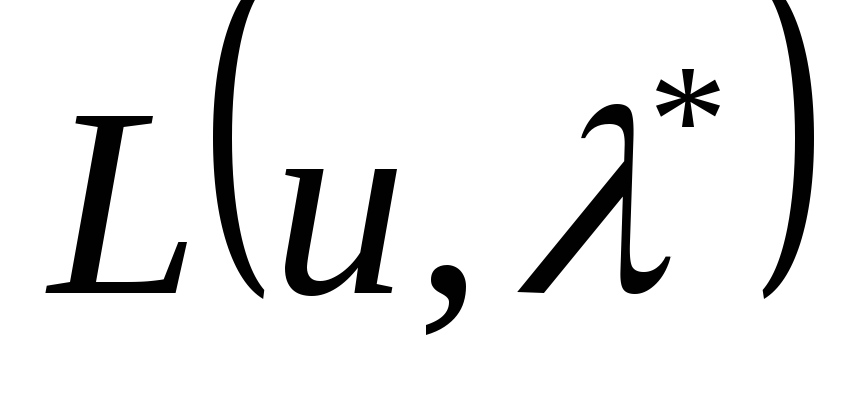
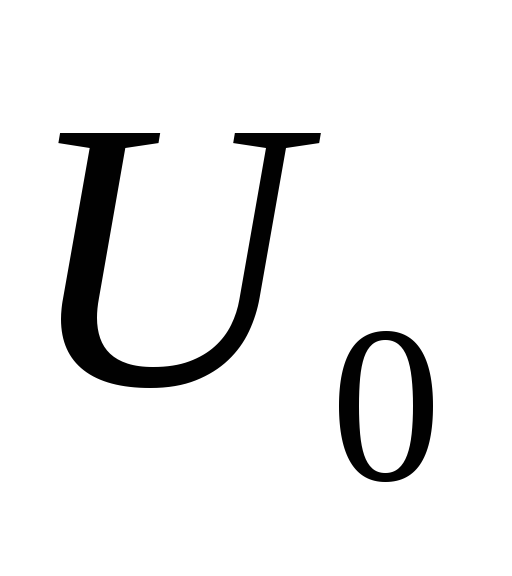 -да
дөңес. Егер
-да
дөңес. Егер
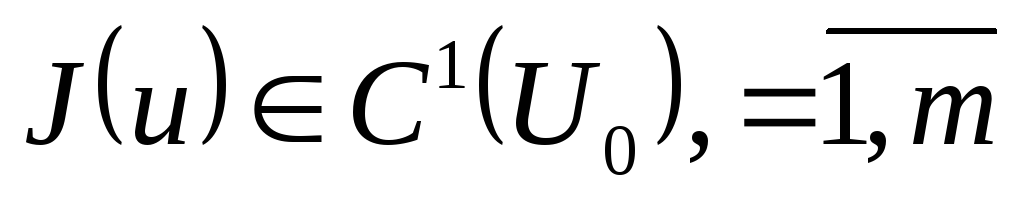 ,
онда тиімділік баламасы бойынша және
глобәлдік минимум туралы теоремадан
(26)-дағы бірінші шартты мынаған
алмастырамыз:
,
онда тиімділік баламасы бойынша және
глобәлдік минимум туралы теоремадан
(26)-дағы бірінші шартты мынаған
алмастырамыз:
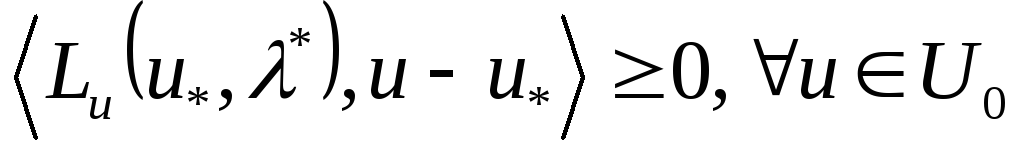 ;
мұндағы
;
мұндағы .
Енді (26)
.
Енді (26) (27) түрінде жазылады.
б)
Егер
(27) түрінде жазылады.
б)
Егер
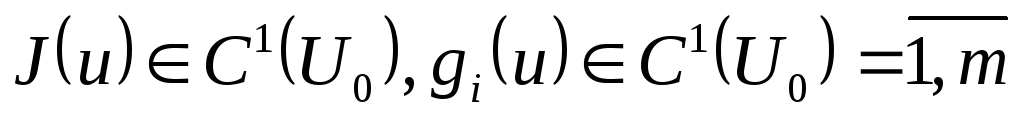 сыртында
сыртында
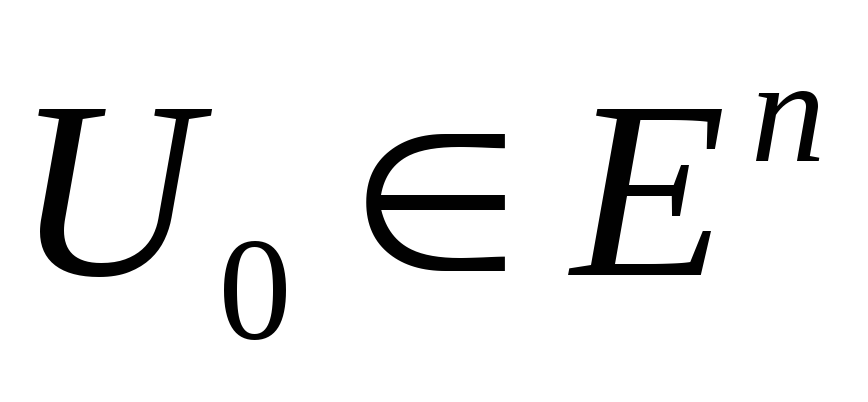 ,
онда тиімділік баламасына сай (27) шартын
келесі түрде өрнектейміз:
,
онда тиімділік баламасына сай (27) шартын
келесі түрде өрнектейміз: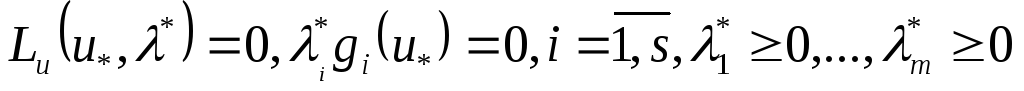 (28) Соңғы (28) шарты
(28) Соңғы (28) шарты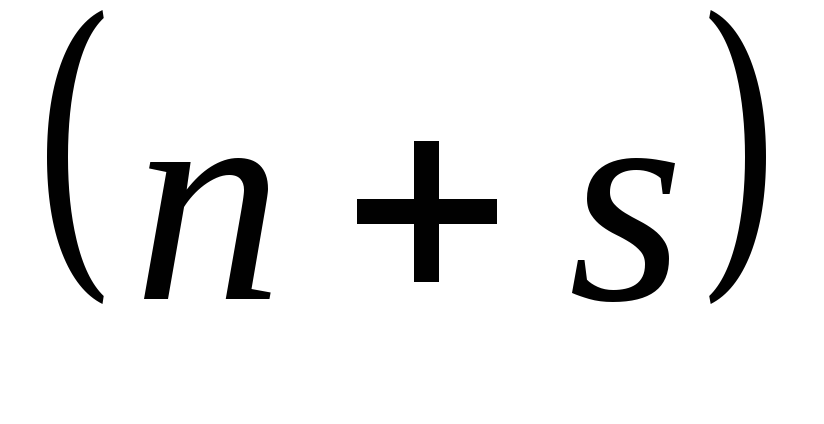 алгебралық теңдеулер жүйесін білдіреді,
алгебралық теңдеулер жүйесін білдіреді,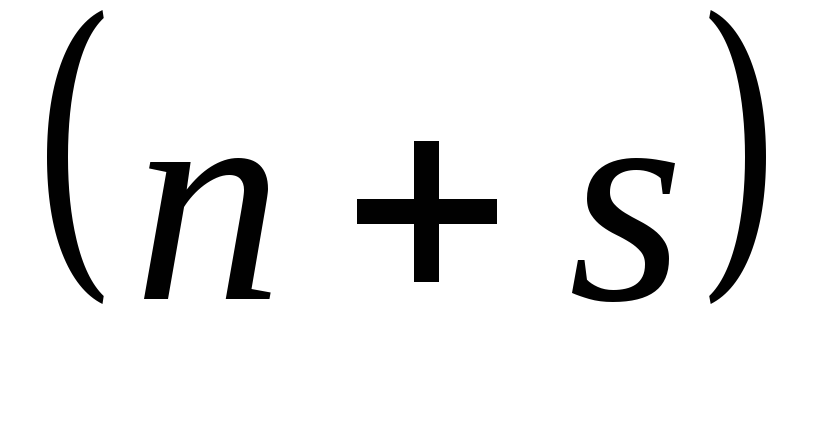 белгісіздер саны:
белгісіздер саны: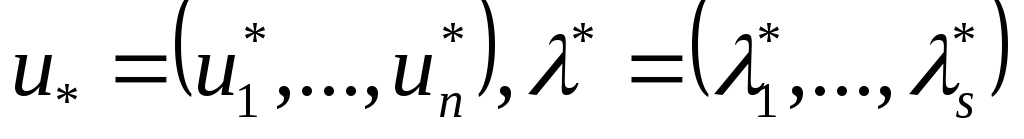 .
Байқайтынымыз: егер Лагранж функциясының
қайқы нүктесі бар болса, онда (28) -
теңдеулер жүйесінің шешімі бар болғаны,
әрі
.
Байқайтынымыз: егер Лагранж функциясының
қайқы нүктесі бар болса, онда (28) -
теңдеулер жүйесінің шешімі бар болғаны,
әрі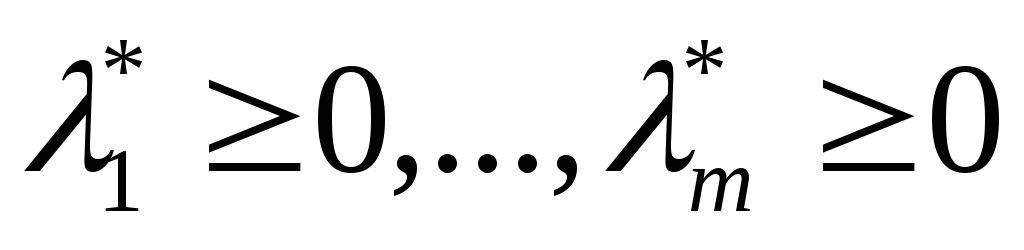 орындалу керек. (28)-шарт
орындалу керек. (28)-шарт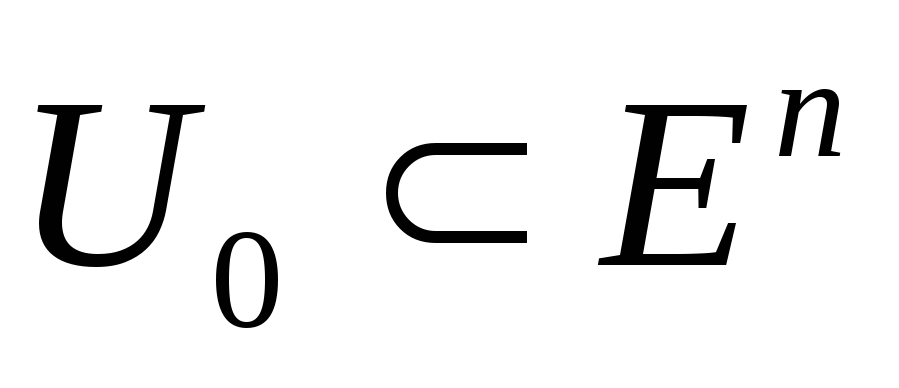 жағдайында қолданылады, дегенмен бұл
жағдайда
жағдайында қолданылады, дегенмен бұл
жағдайда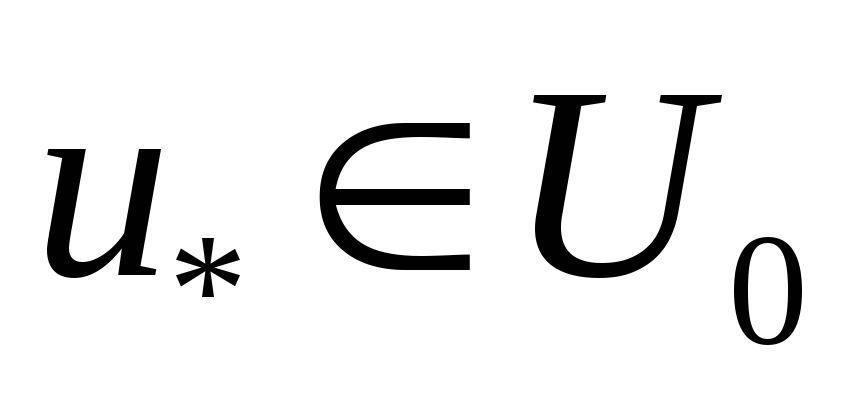 екендігіне көз жеткізу керек.
Мәселен
екендігіне көз жеткізу керек.
Мәселен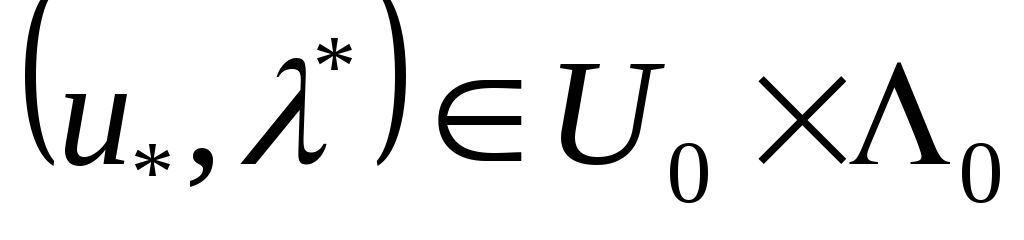 жұбы анықталады дейік. Онда
жұбы анықталады дейік. Онда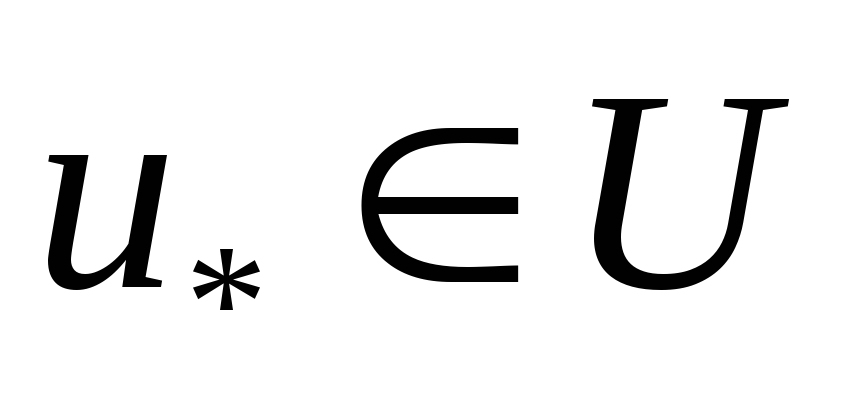 нүктесі мен
нүктесі мен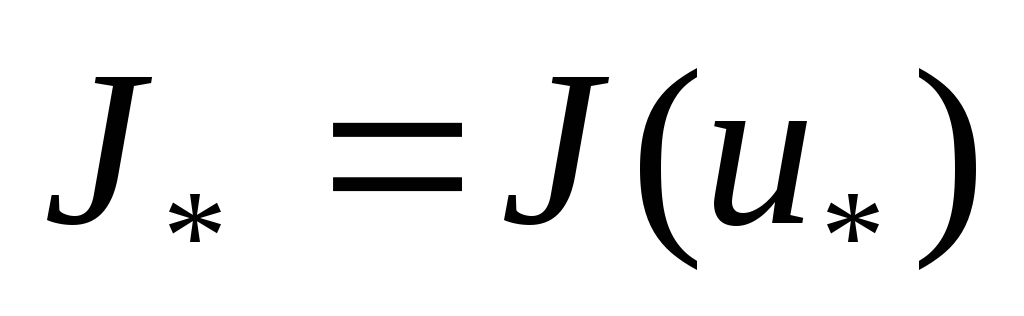 шамасы тиімділік есебінің шешімі (
8-дәрістегі негізгі лемманы қараңыз).
шамасы тиімділік есебінің шешімі (
8-дәрістегі негізгі лемманы қараңыз).
