Дифференциалдық теңдеулер

39. Бірінші ретті туындысы бойынша шешілген сызықтық емес дифференциалдық теңдеулер үшін Коши есебі шешімінің бар болуы және жалғыздығы туралы теорема.

Теорема. Дифференциалдық теңдеу (1) және бастапқы мәндерберілсін.

Егер функциясы мына тұйық облыста

екі шартты қанағаттандырса:

1)қос айнымалы бойынша үзіліссіз;демек

2)айнымалысы бойынша Липшиц шартын қанағаттандырады, яғнисаны бар болып,облысының кез келген екіжәненүктелері үщін

теңсіздігі орындалады, саны нүктелердің алынуына тәуелді емес: онда (1) теңдеудің(2) шартын қанағаттандыратын

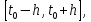
кесіндісінде анықталған, үзіліссіз дифференциалданатын жалғыз ғана шешімі бар болады және

Дәлелдеуі:

Теореманың дәлелдеуін бес кезеңге бөлеміз.

1) Коши есебінің интегралдық теңдеумен эквиваленттілігі.

Айталық (1) теңдеудің (2) шартты қанағаттандыратынкесіндісіндегі шешімі болсын. Яғни

Алынған тепе-теңдікті -ден-ға дейін интегралдасақ, шешімнің

интегралдық тепе-теңдікті қанағаттандыратынын көреміз. Сондықтан (1),(2) Коши есебін (3) интегралдық теңдеуімен алмастыралық. Берілген теңдеудің (2) шартты қанағаттандыратын шешімі (3) теңдеудің шешімі болатыны көрсетіледі. Енді (3) теңдеудің шешімі (1),(2) есептің шешімі болатынын көрсетелік.(3) теңдеудің шешімі болсын. Ондаболады датепе-теңдігі орындалады. Тепе-теңдіктің оң жағы үзіліссіз дифференциалданатын ф-я. Онда сол жағы да үзіліссіз дифференциалданады. Егер тепе-теңдікті дифференциалдасақ,яғни (3) теңдеудің шешімі (1) теңдеудің (2) шартты қанағаттандыратын шешімі болады. Шешімдердің осы көрсетілген ортақтығы мағынасында (1),(2) Коши есебі мен (3) интегралдық теңдеу эквивалентті деп аталады.

2. Дәйекті жуықтау тізбегін құру. Интегралдық (3) теңдеудің шешімін табу үшін Пикардың дәйекті жуықтау әдісін пайдаланамыз. Бастапқы жуықтау ретінде ізделінетін шешімнің алғашқы мәніне тепе-тең болатын функцияны аламыз:

Келесі жуықтауларды мына формулалар

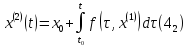
…………………………………….. (4)

арқылы анықтаймыз. Мұнда .Алынғантізбегінің әрбір мүшесі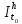кесіндісінде анықталған, үзіліссіз болады және D облысынан шығып кетпейді.

Мұндағы функциясыобл-да анықталған.болғ-н, ол үз-з. Ал онда жоғары шегінің үз-з. Ал онда жоғары шегінің үз-з ф-сы болып табылатын интеграл-

үз-з. Сондықтан үз-з және. Ал-денболғанда

теңсіздігін аламыз. Яғни (

Енді тізбектің үшінші мүшесін

,қарастыралық. Интеграл астындағыф-сыобл-да анықталған. Сондықтан ол үз-з. Ендеше интеграл үз-з, ал онда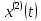үз-з. Ал-денболғанда

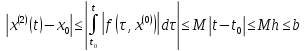
теңсіздігін аламыз. Яғни . Сонымен бірге

Әрбір жуықтау оның алдында тұрған жуықтау арқ анықталғандықтан, матем-қ индукция әдісін пайдаланып үшін дәлелденгендерді тізбектің жалпы мүшесіүшін де дәлелдеуге болады. Шынында дасаны үшіндеп есептесек,-де,болады да,

шығады. Яғни

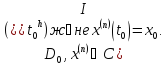
3. Дәйекті жуықтау тізбегінің жинақтылығы. Құрылған тізбектің кес-де жинақты болатынын көрсетелік.Ол үшінбөлікке

қосындысы -мүшесі-ге тең болатын функциялық қатар

(6) қарастырамыз. Бұл (6) қатардың бірқалыпты жинақтылығынан (5) тіз-ң бірқалыпты жинақты-ғы шығады себебі

Қатар әрбір мүшесін екіншісінен бастап кес-де абсолют шамасы бой-ша бағалайық

Енді функция Липшиц шартын қанағаттандыратынын пайдаланалық. Онда қатардың екінші мүшесі үшін алынған бағаны ескеріп мына теңсіздікті

Қатардың кез келген n мүшесі үшін де осындай теңсіздік орындалады. Оны мат-қ индукция әдісімен көрсетуге болады.

Сонымен (6) қатардың мүшелерінің абсолют шамасынан құрылған қатар кес-де мына теңсіздікті қанағаттандырады:

Теңсіздіктің оң жағындағы сандық қатар жинақты. Оны Даламбер белгісіне сүйеніп дәлелдейміз.

Онда Вейерштрасс белгісі бой-ша функ-қ қатар кес-де бірқалыпты жинақты. Егер қатардың қосындысындеп белгілесек, онда (5) тізбектің шегі осы функ-ға тең болады:жәнеКез келгенүшін

болғанда шекке көшіп теңдігін, яғни шектік функ-ң да (2) бастапқы шартты қанағаттандыратынын аламыз.Егертеңсіздігінде шекке көшсектеңсіздігін аламыз,яғни

4) Шектік ф-я-(3) теңдеудің шешімі

Липшиц шартын пайдаланып

теңдігін аламыз.Бұдан

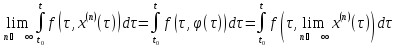теңдігі алынады. Оны пайдаланып (4) жүйедегі -ы анықтайтынтеңдеуіне көшсек

тепе-теңдігін аламыз.Яғни функ-сы -кесіндісінгі (3) интегралдық теңд-ң шешімі. Олай болсафунк-сы -кесіндісінде анықталған (1),(2) Коши есебінің шешімі.

5) Шешімнің жалғыздығы Коши есебінің шешімінің жалғыздығын дәлелдемес бұрын Гронуолл леммасын дәлелдейік.

Гронуолл леммасы. Егер үз-з функциялары жәнетұрақтысы үшін

(7)

теңсіздігі орындалатын болса, онда

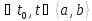,(8) теңсіздігі орындалды.

Дәлелдеуі:

Лемманың әуелі болатын кезде дәлелдейік.Берілген (7) теңсіздікті оң жағындағы қосындыға бөліп

теңсіздігін аламыз.Бұдан екі жағында функ-на көбейту арқылы

алынады.Бөлшектің бөлімінің туындысы алымына тең. Осыны ескеріп соңғы теңсіздікті дейін интегралдасақ

теңсіздігін аламыз.Потенциалдап,онан соң (7) теңсіздікті пайдалансақ

Лемма болған кезде дәлелденді. Лемманыболған кезде дәлелдеу үшін келтірілген дәлелдеудегі-ны орындарымен ауыстырса болғаны. Егер (7) және (8) формулалардакезде шекке көшсек лемманыңболғанда да дұрыс болатынын көреміз. Бұл жағдайда

Енді шешімнің жалғыздығын дәлелдейміз. Коши есебініңкес-де анықталғаншешімінен басқашешімі болсын.Оның

анықталу кесіндісін арқылы белгілейік.Онда олар үшін мына тепе-теңдіктер

орындалады.Бұл теңдіктерден кес-де

теңсіздігі алынады. Бұған Гронуолл леммасын қолданып

яғни

тепе-теңдігін аламыз.Теорема дәлелденді.

40.-Ші ретті сызықты дифференциалдық теңдеудің жалпы шешімінің құрылымы.

коэффиценттері,бос мүше.

болған жағдайда теңдеудің екі жағын соған бөлсек

(1),(2)-n-ретті сызықтық біртекті емес дифференциалдық теңдеу.

(2) ге сәйкес мына теңдеу

(3)

n-ретті сызықтық біртекті дифференциялдық теңдеу.

Егер 𝜓(t) біртекті емес теңдеудің дербес шешімі,ал біртекті (3) теңдеудің жалпы шешімі болса онда сызықты дифференциалдық теңдеудің жалпы шешімі

болады. Коэффициенттері (a,b) аралығында үзіліссіз кез келген сызықты біртекті теңдеудің базисы бар болса, онда –теңдеулердің жалпы шешімі мына түрде

болады. Мұндағы еркін тұрақтылар.

41. Сызықты дифференциалдық жүйенің жалпы шешімінің құрылымы.

Сызықтық біртекті

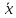=(1)

Жүйеде n-ретті квадраттық комплекс(не нақты) матрица

. жүйенің шешімінің базисы болсын,онда жүйенің жалпы шешімі

түрде анықталады. Мұндағы кез келген еркін түрақты векторлар.

Сызықтық біртекті емес дифференциалдық жүйе қарастырайық :

(2)

Мұнда n-ретті квадраттық комплекс(не нақты) матрица, .

Егер - (1)жүйенің шешімі,ал сәйкес біртекті жүйенің

=

Шешімі болса, онда

+(3)

вектор-функциясы (1) жүйенің жалпы шешімі болады.

42.Тұрақты коэффициентті сызықтық біртекті дифференциалдық теңдеулердің шешімі.

Егер

++…++

сызықтық теңдеуінің коэффиценттері тұрақтыға тепе-тең болса,онда олкоэффиценттері тұрақты сызықтық дифференциалдық теңдеу деп аталады. Біз коэффициенттері тұрақты сызықтық біртекті

++…++

теңдеуін қарастырамыз және коэффициенттері нақты сандар деп есептейміз. Теңдеудің ретіболса,Әрбір-ретке дейін дифференциалданатынфункциясына оның туындыларын сәйкес қоятын дифференциалдық оператор

енгізу арқылы (1) теңдеуді былайша жазуға болады:

++…++

.

Ал

(2)

белгілеуін енгізу аркылы (1) теңдеуді ықшам түрге

келтіруге болады. Әдетте (2) формула бойынша анықталған өрнегінстационар (коэффиценттері тұрақты) дифференциалдық оператор немесе операторлық көпмүшелік деп атайды.

Төменде (1) теңдеудің базисін құру үшін - дәрежелі алгебралық теңдеудің түбірлерін табу жеткілікті екені көрсетіледі.

Әрбіроператорына немесе (1) теңдеуге белгісіз параметр λ бойынша жазылган

()

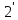көпмүшелігін сәйкес қоямыз. Бұл көпмүшелікті құру үшін операторындағы-ретті туындыны параметр-ның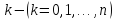дәрежесімен ауыстыру жеткілікті. Әдетте бұлкөпмүшелігі сипаттаушы көпмүшелік деп аталады.

Егер болса (1) теңдеу бірінші ретті сызықтық теңдеуге

айналатын еді де, оның жалпы шешімі

функциясы болар еді. Шешімнің бұл түрі (1) теңдеудің шешімдерін болған жағдайда да көрсеткіштік функция көмегімен іздеуге нұсқайды. Эйлер көрсетуі бойынша (1) теңдеудің дербес шешімін мына түрде іздейміз:

(3)

Мұндағы -ретке дейін дифференциалданатын жаңа функция,- жоғарыда аталған белгісіз нақты не комплекс сан.

(4)

теңдеуінің түбірі болғанда ғана функциясы (1) теңдеудің шешімі болатыны алынады. (4) теңдеу сипаттаушы теңдеу, ал оның түбірлері сипаттағыш сандар деп аталады. Сипаттаушы теңдеу түбірлерінің әр түрлі не еселі болуына байланысты екі жағдай қарастырылады.

1-жағдай. Сипаттағыш сандар әр түрлі, яғни

болсын. Онда Бұл жағдайда әрбірүшін:

(*)

Бұл теңдеудің кез келген үшінфункциясы шешімі болатыны көрініп тұр. Табылғанжәнемәндерін әрбірүшін (3) формулаға қойып, (1) теңдеудіңшешімін аламыз:

(5)

Бұл шешімдер -де нақты не комплекс сандар өрісіне қатысты сызықтық тәуелсіз. Егернақты сандар болса, онда (5) шешімдер нақты шешімдер болады. Олар-де сызықтық тәуелсіз болғандықтан, базис құрайды. Сондықтан (1) теңдеудің жалпы шешімі бұл жағдайда

болады. -нақты еркін тұрақтылар.

Енді түбірлер ішінде комплекс мәнділері бар болсын.

осындай комплекс түбірлердің бірі болсын. Оның түйіндес мәні де (4) теңдеудің түбірі болады. Себебі (4) теңдеудің коэффициенттері нақты сандар. Шешімдерінің (5) формуласы бойыншатүбіріне

комплекс шешімі сәйкес келеді.Коэффициенттері нақты сандар болатын сызықтық біртекті теңдеудің комплекс шешімінің нақты ж/е жорамал бөліктері өз алдарына шешім болатыны белгілі. Сондықтан 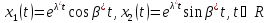(6)

функциялары- (1) теңдеудің нақты шешімдері.

Сонымен барлық сипаттағыш сандар әр түрлі болған жағдайда оларға мына түрдегі

сызықтық тәуелсіз нақты шешімдер сәйкес келеді. Олардың кез келген тұрақты нақты коэффициенттер арқылы құрылған сызықтық комбинациясы (1) теңдеудің нақты жалпы шешімін береді.

2-жағдай.Сипаттағыш сандардың арасында өзара теңдері бар.сипаттаушы теңдеудіңеселі нақты не комплекс түбірі болсын. ОндаБірақ

Сондықтан 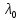үшін жазылатын теңдеудің түрі мынадай болады:

(**)

Бұл теңдеудің шешімдері бар екені көрініп тұр.-де сызықтық тәуелсіз. Шешімдердің (3) формуласына λмәнін ж/е табылған-тің мәндерін кезегімен қойып (1) теңдеудің дара шешімін аламыз:

(7)

Егер саны сипаттаушы теңдеудіңеселі түбірі болса, шешімдердің (7) формуласы бойынша

шешімдері сәйкес келеді. Олардың нақты ж/е жорамал бөліктерін ажыратып мынадай нақты шешімдер аламыз:

; (8)

43.Тұрақты коэффициентті сызықтық біртекті дифференциалдық теңдеулер жүйесінің іргелі шешімдер жүйесін құру. Сипаттаушы теңдеудің әртүрлі түбірлері болатын жағдай.

Коэффициенттері нақты сандар болатын сызықтық біртекті дифференциалдық жүйе берілсін: (1)

Мұнда

Эйлер нұсқауы бойынша жүйенің шешімін (2)

түрінде іздейміз. мұндағы 0-ге тең болмайтын белгісіз тұрақты вектор,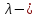белгісіз параметр. Жүйеге (2) ауыстыруды апарып қойсақ,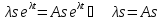теңдігі алынады. Олай болса,векторы ()(3) алгебралық теңдеуінің шешімі болу керек. Ал ол шешім 0-дік болмауы үшін det()(4) теңдігі орындалуы қажет. (4) теңдеу (1) жүйенің сипаттаушы теңдеуі деп, ал оның түбірлері сипаттағыш сандар деп аталады.

Барлық сипаттағыш сандар әр түрлі болатын жағдайды қарастыралық. Әрбір

санына (3) теңдеуден,оған -ның орнына-ді қойғанда алынатынматрицасының меншіктівекторы сәйкес келеді.

Әр түрлі меншікті сандарға сәйкес табылатын меншікті векторлар да өзара сызықтық тәуелсіз болады. Түбірлер әр түрлі болған жағдайда .

Сондықтан меншікті векторлар (3) теңдеуден тұрақты көбейткіштерге дейінгі дәлдікпен табылады. Табылған меншікті сандар мен меншікті векторларды кезегімен (2) формулаға қойып, (1) жүйенің мынадай шешімдерін аламыз:

(5)

Мұнда ,

,,

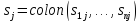Алынған шешімдер -де (1) жүйенің шешімдердің іргелік жүйесін құрады.

Бұны дәлелдеу үшін (5) шешімдердің вронскианыннүктесінде қарастыралық:

Ол 0-ге тең емес, себебі анықтауыштың тік жолдары өзара сызықтық тәуелсіз. Енді коэффициенттері тұрақты сызықтық біртекті жүйенің кез келген шешімі -де анықталатынын ескерсеквронскианы да-де 0-ге тең болмайды. Шынында да,

Сонымен (5) шешімдер базис құрағандықтан, (1) жүйенің жалпы шешімі олардың кез келген тұрақты коэффициенттер арқылы өрнектелетін сызықтық комбинациясына тең болады:

Енді сипаттаушы теңдеу түбірлерінің комплекс мәнділерін қарастырайық.

Комплекс мәнді меншікті сандарға сәйкес келетін нақты шешімдерді құру жолын көрсетелік. сипаттаушы теңдеудің жай комплекс түбірі болсын және оған сәйкес табылған меншікті векторболсын.Онда (5) формула бойынша жүйенің мына комплекс шешімін аламыз

)))

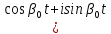аламыз. Жүйенің коэффиценттері, яғни А матрицасы нақты болғандықтан бұл комплекс шешімнің нақты ж/е жорамал бөліктері өз алдына нақты шешім болады. Сондықтан (1) жүйенің

(6)