Метод элементарных преобразований. (Метод Гаусса)

Определение: Назовем прямоугольную матрицу ступенчатой если каждая её строка имеет не нулевой элемент и первый не нулевой элемент каждой строки начинается со 2-й расположенной правее 1 и 0 элемент предыдущей строки. В частности квадратная ступенчатая матрица называется треугольной. Из этого определения следует: число строк ступенчатой матрицы не превосходит числа её столбцов.

Элементарные преобразования строк матрицы:

1)перестановка 2-х строк матрицы

2)умножение любой строки матрицы на число < >0.

3)прибавление к элементам любой строки матрицы соответствующих элементов другой строки умноженных на одно и то же число

Теорема: Всякую не нулевую матрицу А можно привести к ступенчатому виду с помощью элементарных преобразований строк и отбрасыванием нулевых строк

№13-14-----------------------------------------------------------------------

Системы линейных уравнений. Критерий совместности и критерий определенности.

Общий вид системы линейных уравнений:

(1)

()- решение системы –упорядоченная совокупность чисел, которые при подставлении в сумму вместо обращает уравнения системы (1) в верное равенство.

Запишем матрицу системы (1), добавив справа столбец свободных членов:

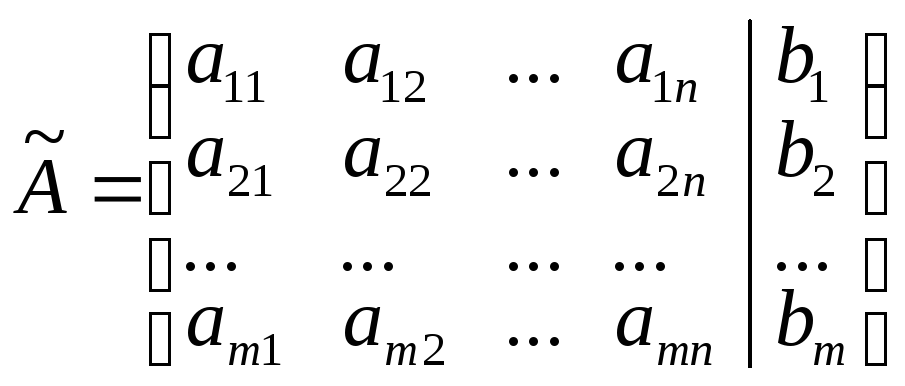(2)

Матрица (2) расширенная матрица системы линейных уравнений.

Определение: Если в системе все b_к (k=1,...m) равны нулю, то такая система называется однородной. Если хотя бы один из них b_к0, то система называется неоднородной.

Определение: Система называется совместной, если она имеет хотя бы одно решение, в противном случае она называется несовместной.

Определение: Совместная система линейных уравнений называется определённой, если она имеет единственное решение и неопределённой - если решений множество.

Критерий совместности (Теорема Кронекера-Капелли): для того, чтобы система уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы и ранг расширенной матрицы были равны. ( или противоречива: ).

Доказательство: Необходимость. Пусть сумма (1)-совместна, докажем что , т.е. есть решения () и . Из последнего столбца м. вычтем линейную комбинацию столбцов матрицы A, получим матрицу

.

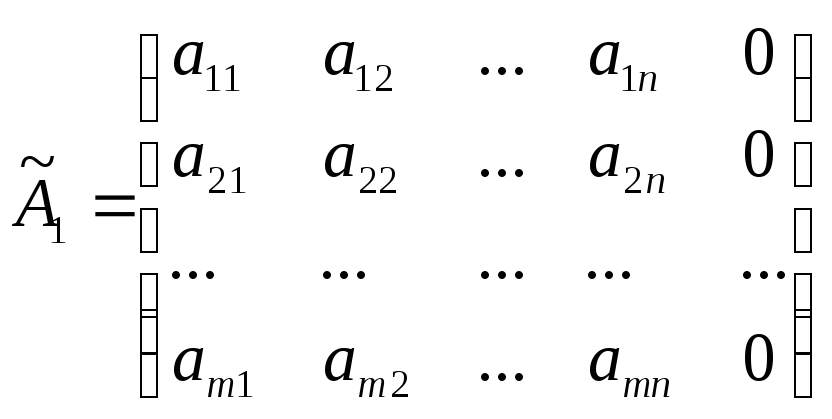
Достаточность. Пусть , докажем, что сумма совместна. Т.к. , то существует минор , который является базисным. На основании теоремы о базисном миноре последний столбец матрицы является линейной комбинацией остальных столбцов матрицы.

()- решение системы (1), т.е. система (1)-совместна.

Критерий определённости. Совместная система является определенной, если и неопределенной, если .( n – кол-во неизвестных.)

Доказательство а) Пусть - это значит, что столбцы матрицы A линейно зависимы, т.е. существуют числа не все равные нулю и такие, что (*). По условию система 1 совместна, т.е. существуют решения () системы (1)

(**). (*)+(**)=,т.е. - решение системы (1).

б) Пусть r =n (значит ), докажем, что сумма (1) – определена.

Пусть решений два, тогда ,,хотя бы одно , тогда ,но так как ранг матрицы А равен n ,то все столбцы матрицы А линейно независимы, значит линейная комбинация этих столбцов = 0, только когда все коэффициенты = 0, т.е. , …- противоречие => 1 решение.(ч.т.д.)

Замечание: Неопределённая сумма имеет б.много решений, т.к. из (*) и (**)следует, что , где k=0,1,-1,2,-2,… - является решениями.

№15-16-----------------------------------------------------------------------