2. Если линия на плоскости в некоторой дск может быть задана уравнением вида (2) то и в любой другой дск она может быть задана уравнением того же вида имеющим туже степень.

Доказательство: Обе теоремы доказываются одинаково. Докажем теорему 2. С этой целью перейдем от ДСК о которой речь шла в определении к произвольной новой ДСК. Новые координаты 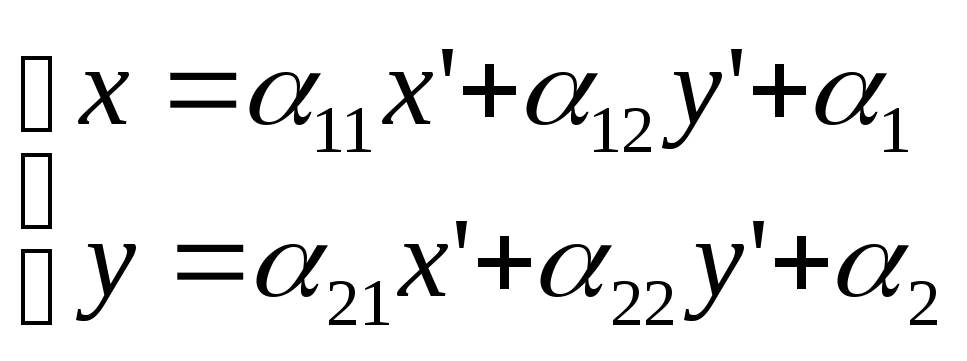. тобы получить новое уравнение линии нужно x и y подставить в (2). Ясно что при этом превратится в многочлен в степени (k+e). Степень суммы многочленов не превышает степени старшего члена( степень могла бы понизиться если бы члены с наибольшей степенью взаимно уничтожились). Таким образом мы доказали пока что алгебраическая линия в любой ДСК имеет уравнение вида (2) причем степень уравнения при переходе от одной ДСК к другой не может повыситься. Остается доказать что она не может и понизиться и должна оставаться постоянной. Предположим противное, что при переходе от одной СК к другой степень понизилась, тогда при обратном переходе она должна повыситься что невозможно.(ч.т.д.)

№31---------------------------------------------------------------------------

Доказать,что в о.д.с.к. на плоскости(в пространстве) каждая прямая линия(плоскость) может быть задана линейным уравнением; обратно : каждое линейное уравнение в о.д.с.к. на плоскости(в пространстве) определяет прямую линию(плоскость).

Уравнения первой степени или линейные уравнения связывающие координаты точки в пространстве имеют вид . Аналогично на плоскости .

Теорема1: В общей ДСК в пространстве каждая плоскость может быть задана линейным уравнением (1). Обратно каждое линейное уравнение (1) в ОДСК определяет плоскость.

Теорема2: В ОДСК на плоскости каждая прямая линия может быть задана уравнением(2). Обратно каждое линейное уравнение (2) в ОДСК на плоскости определяет прямую линию.

Доказательство: Обе теоремы доказываются одинаково. Докажем теорему 1. Пусть задана некоторая плоскость. Систему координат выберем так: точка О и два базисных вектора поместим в плоскость, а вектор выполним произвольно. В такой СК наша плоскость будет иметь линейное уравнение Z=0. В силу теоремы об инвариантности наша плоскость будет иметь линейное уравнение и в любой другой ДСК.

Обратно пусть мы имеем ОДСК и линейное уравнение(1). Докажем что это линейное уравнение определяет плоскость. Перейдем к другой ДСК. Для определенности пусть С≠0. Сделаем замену переменных: 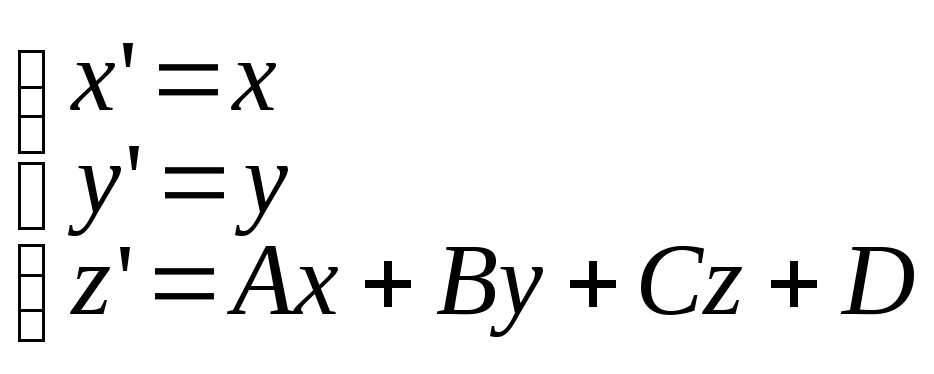. Покажем что эта система равенств определяет переход к новой системе координат( выражает связь между старыми и новыми координатами точки). .

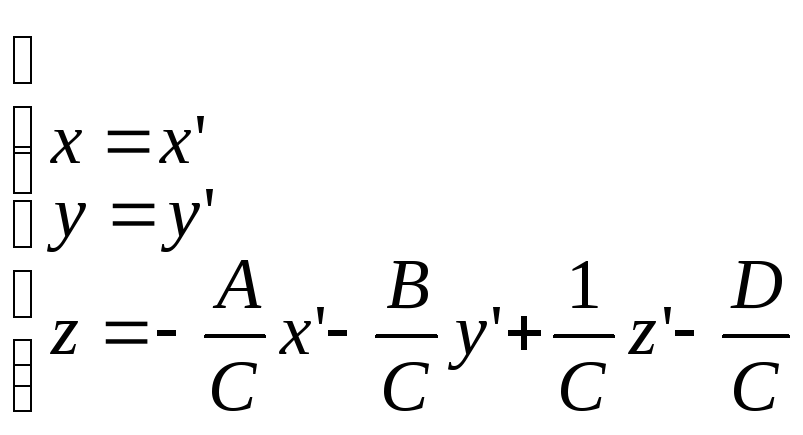Переход к новой СК:

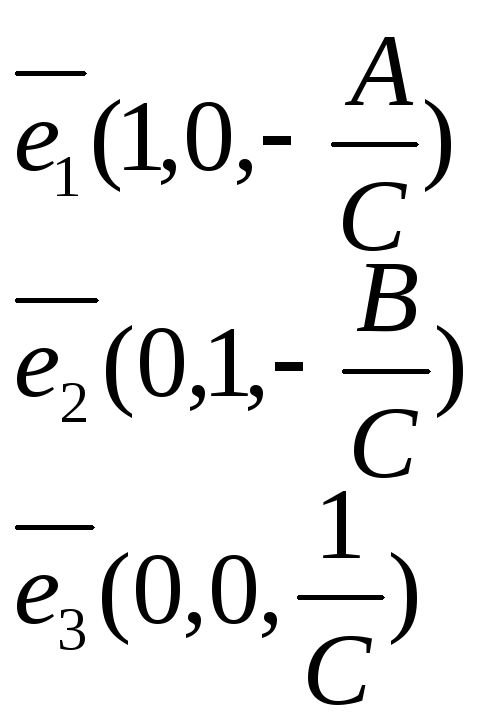
Новое начало СК в старой системе . Уравнение плоскости будет иметь уравнение(т.е. уравнение (1) переходит в новой СК в уравнение) Z’=0. Значит и уравнение(1) определяет плоскость. (ч.т.д.)

Уравнение (1) и (2) называются общими уравнениями плоскости и прямой на плоскости соответственно.

№32---------дописать-----------------------------------------------------

Параметрические уравнения прямой и плоскости.

А)Параметрические уравнения прямой. Прямая линия на плоскости или в пространстве полностью определяется точкой, лежащей на этой прямой( начальная точка) и вектором, параллельным этой прямой(направляющим вектором). Аналогично плоскость полностью определяется точкой принадлежащей плоскости и двумя неколлинеарными векторами в этой плоскости(начальная точка и направляющие вектора в плоскости). Рассмотрим точку М радиус вектор которой . Ясно что точка М будет принадлежать прямой тогда и только тогда когда , где t - некоторое определенное вещественное число. Другими словами для любой точки М принадлежащей прямой существует t, такое что имеет место (4) и наоборот, какое бы число t мы не подставили в (4) вместо t, вектор определяемый (4) будет радиус-вектором некоторой точки на прямой.

В формуле (4) переменная величина t пробегающая все вещественные значения называется параметром. А уравнение (4) векторно-параметрическим уравнением прямой. Векторно-параметрическое уравнение прямой выглядит одинаково и для прямой на плоскости и в пространстве. Но при разложении по базису оно сводится в одном случае к двум а в другом к трем скалярным уравнениям. В пространстве: 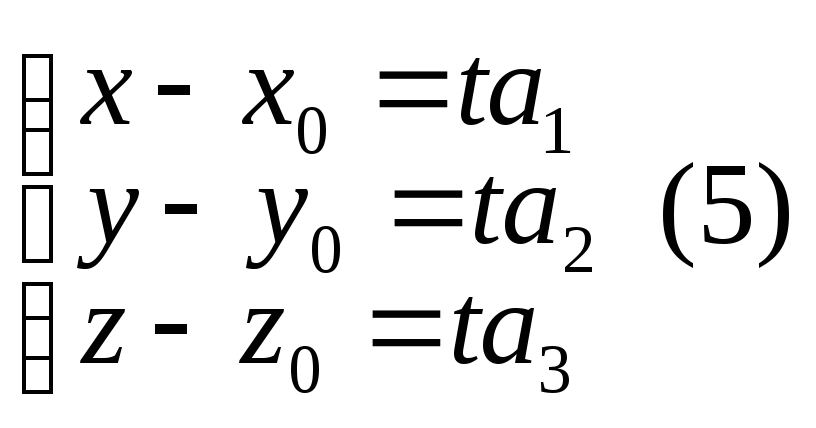- параметрические уравнения прямой в пространстве.

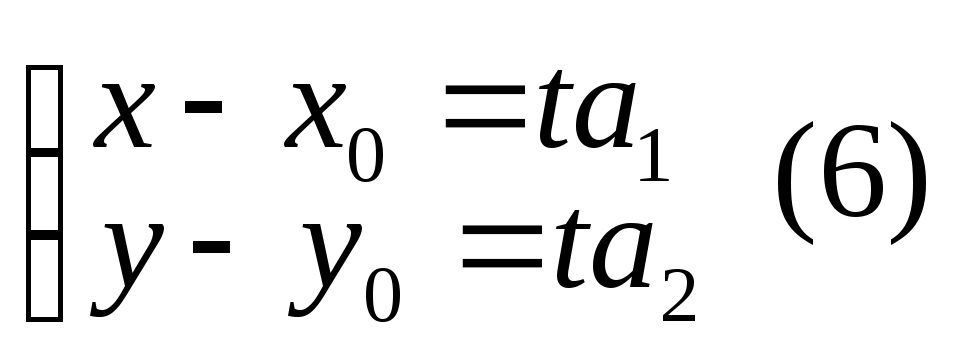- параметрические уравнения прямой на плоскости.

Б) Пусть точка М произвольная точка в пространстве. Начало вектора лежит в плоскости следовательно его конец – точка М лежит на плоскости тогда и только тогда когда этот вектор лежит в рассматриваемой плоскости. Поэтому точка М лежит в плоскости тогда и только тогда когда найдутся t₁ и t₂, такие что . Другими словами точка М с радиус вектором принадлежит плоскости тогда и только тогда когда существуют t₁ и t₂, такие что выполняется (7). И наоборот, какие бы числа мы не подставили в (7) вместо t₁ и t₂ вектор определенный уравнением (7) будет радиус-вектором точки лежащей в плоскости. Переменные t₁ и t₂ пробегающие все вещественные значения называются параметрами. А уравнение (7) называется векторно-параметрическим уравнением плоскости. 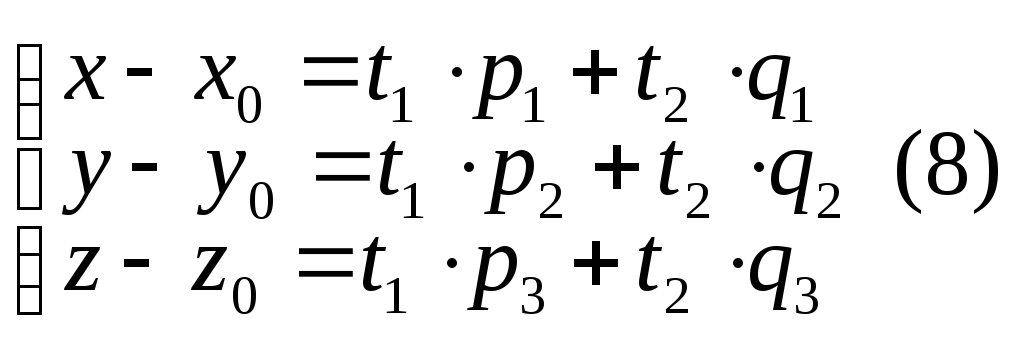Уравнение (7) эквивалентно трем скалярным уравнениям - параметрические уравнения плоскости.

№33---------------------------------------------------------------------------