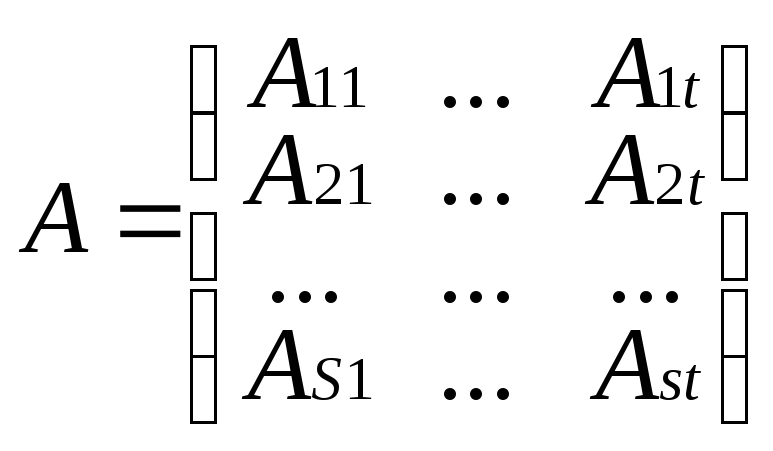
Блочные матрицы. Сложение и умножение блочных матриц. Теорема об определителе квазитреугольной матрицы.

Прямоугольную матрицу А можно вертикальными и горизонтальными линиями разбить на прямоугольные клетки(блоки). В частности матрица может быть разбита только горизонтальными или только вертикальными линиями. (А_α,β)_s,t – блочная матрица. Рассмотрим две матрицы А и В одинаковой размерности и с одинаковым разбиением на блоки. Соответствующие блоки А_α,β и В_α,β имеют одинаковую размерность m_α x n _β , α=1..s, β=1..t. Тогда в соответствии с правилом сложения матриц операция сложения блочных матриц одинаковых размеров с одинаковым разбиением на блоки, производится точно также как если бы вместо блоков стояли числовые элементы.

Чтобы распространить правило умножения матриц на блочные матрицы необходимо чтобы все горизонтальные размеры блоков первой матрицы совпали с соответствующими размерами второго сомножителя. Число столбцов блока А_α,β равно числу строк блока В_β,с .

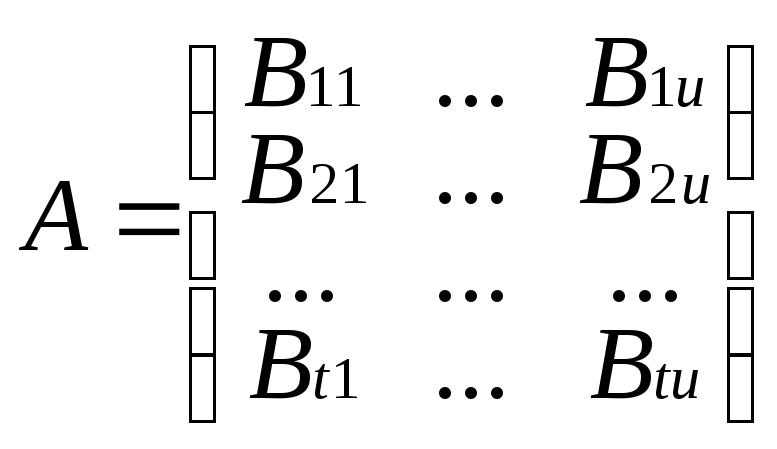
b изменяется от 1 до t, с изменяется от 1 до u. Таким образом возможно умножение матриц А и В формально также как если бы вместо блоков стояли числовые элементы.

Определение: Квадратная матрица у которой все элементы расположенные под(над) главной диагональю равны 0 называется верхней(нижней) треугольной матрицей. Аналогичные понятия вводятся и для блочных матриц.

Определение: Блочная матрица А называется верхней(нижней) квазитреугольной матрицей если все диагональные блоки и сама матрица А квадратные матрицы, и все не диагональные блоки расположенные под(над) диагональными блоками нулевые матрицы.

Определение: Блочная матрица А называется квазидиагональной если все диагональные блоки и сама матрица А квадратные матрицы, а все недиагональные блоки – нулевые матрицы.

Теорема: Определитель квазитреугольной матрицы связан с определителем диагональных матриц следующим соотношением:

(♀) где П – произведение.

Доказательство: Рассмотрим сначала квазитреугольную матрицу где А₁₂=0, , ,

По определению

Т.к. А₁₂=0 то из всех произведений могут быть ≠0 только те в которых индексы . Вследствие этого остальные индексы могут принимать значения только из множества . В этих условиях число инверсий в перестановке равно:

т.е.

№7-продолжение---------------------------------------------------------

Учитывая это находим, что

Отсюда следует что

Рассматривая в общем случае квазитреугольную матрицу

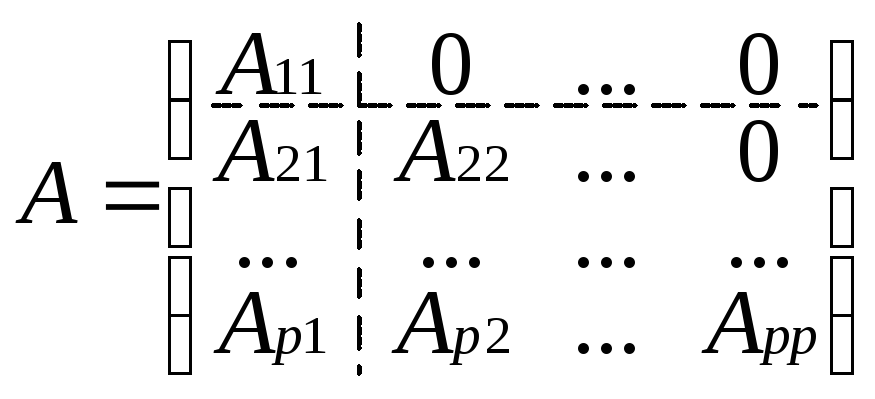
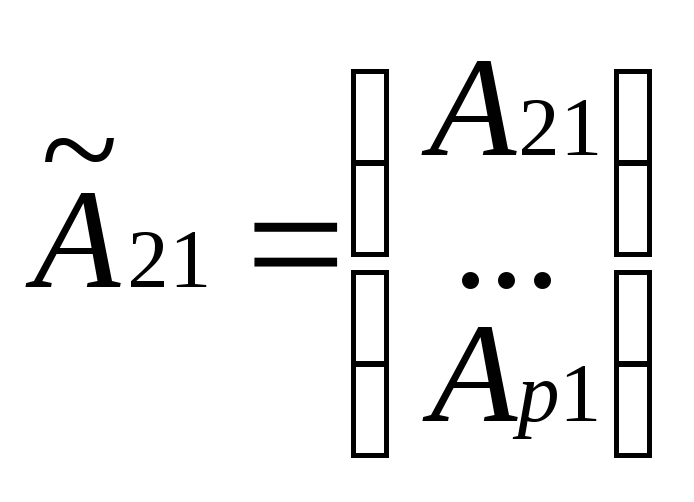
Как матрицу где согласно (*) будем иметь . Матрица снова квазитреугольная. Проделав над ней туже операцию, получим . После (р-1) таких шагов придем к (♀).

Аналогично доказывается равенство (♀) применительно к верхней квазитреугольной матрице.(ч.т.д.)

№8----------------------------------------------------------------------------Теорема об определителе произведения матриц.

Теорема:

Доказательство: Пусть заданы квадратные матрицы порядка n. и . На основании теоремы об определителе квазитреугольной матрицы () имеем: 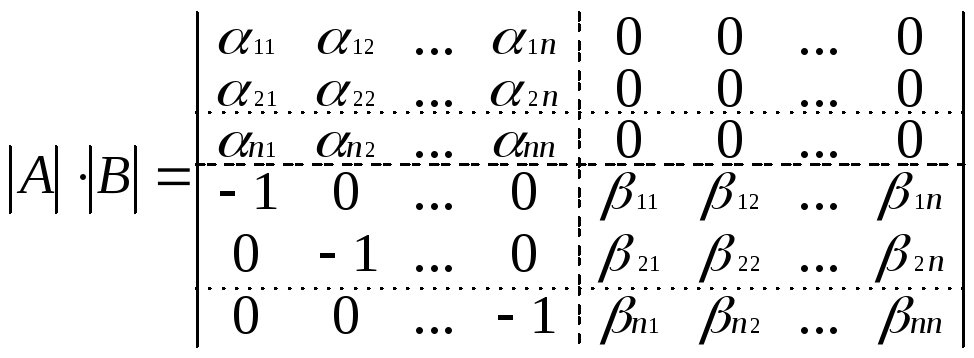порядок данной матрицы 2n. Не изменяя определителя, над матрицей порядка 2n выполним последовательно следующие преобразования: к первой строке прибавим . В результате такого преобразования на первых n позициях первой строки будут все 0, а на вторых(во втором блоке) – будет стоять сумма произведений первой строки матрицы А на первый столбец матрицы В. Проделав те же самые преобразования с 2 … n строками получим следующее равенство:

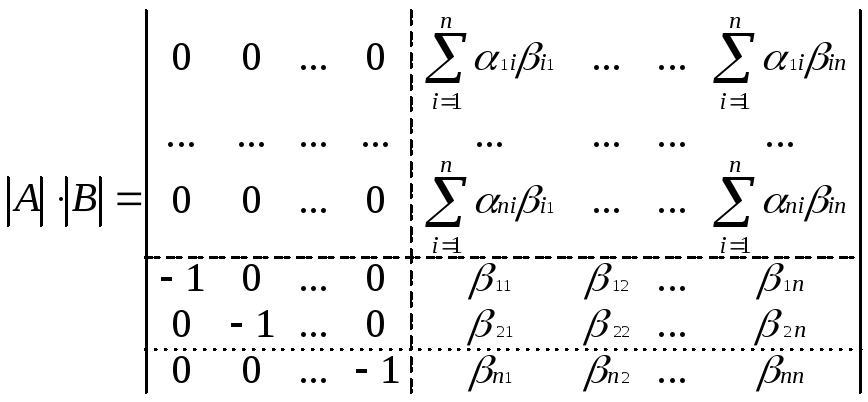
Чтобы привести правый определитель к квазитреугольному виду поменяем в нем местами 1 и 1+ n столбцы, 2 и 2+ n … n и 2 n столбцы. В результате получим равенство:

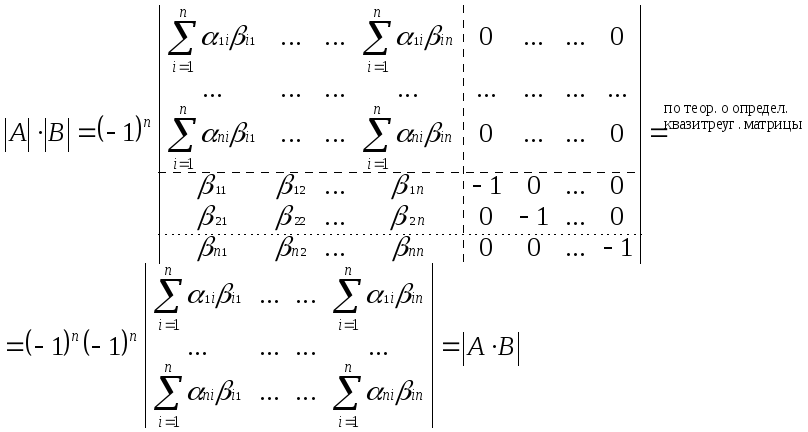
Замечание: Ясно что теорема справедлива для любого конечного числа матриц. В частности .

№9----------------------------------------------------------------------------