Cвойства линейных операций над векторами

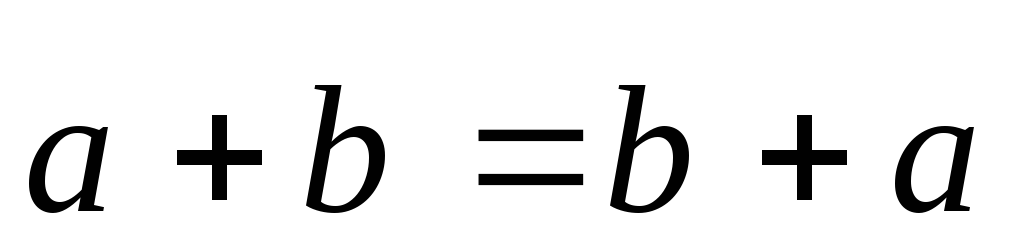1. (коммутативность).

Доказательство: Это свойство доказывается геометрическим построением.

Э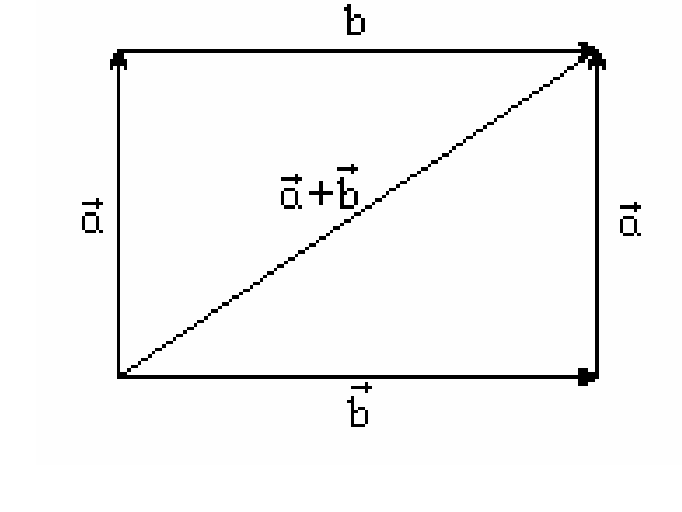ти свойства позволяют оперировать с векторами так же как и с вещественными числами.

2. (ассоциативность).

Доказательство: Рассмотрим

(ч.т.д.)

По индукции может быть определена сумма любого числа векторов: a1+ a2+ a3+ a4= ((a1+ a2)+ a3)+ a4= (a1+ a2+ a3)+ a4= (a1+ (a2+ a3))+ a4= a1+ ((a2+ a3)+ a4)= a1+ (a2+ (a3+ a4))= (a1+ a2)+ (a3+ a4)

При этом в силу коммутативности можно произвольно менять порядок слагаемых, из сказанного вытекает следующее правило замыкающего вектора: Для того чтобы сложить n векторов нужно записать их в любом порядке. Приложить первый вектор к какой-нибудь точке О, а каждый следующий к концу предыдущего, тогда замыкающий вектор ОА_n и будет их суммой.

3. .

4. .

5.а=(а)

6. (+)а=а+а(дистрибутивность относительно сложения чисел)

7. (а+b)= а+b (дистрибутивность относительно сложения векторов)

8. 1*a=a

№21---------------------------------------------------------------------------

Теорема о существовании и единственности разности двух векторов.

Определение: Разностью двух векторов а и b называется такой вектор от прибавления которого к b получается а.

Д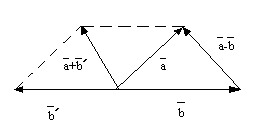ля того чтобы получить а-b надо отложить от одной точки а и b, построить на этих сторонах параллелограмм, тогда вектор диагональ направленный в сторону уменьшающегося вектора является разностью векторов.

Теорема. Для любых векторов а и b, а-b существует и единственно, и выражается формулой а-b=а+(-b)

Доказательство. b+(а+(-b))= b((-b)+a)= (b+(-b))+a=0+a=a

Убедимся теперь в единственности.

Пусть наряду с с=а+(-b) существует d такой что b+d=a

(d+b)+(-b)= d+(b+(-b))=d+0=d

(d+b)+(-b)=a+(-b)=c следовательно с=d (ч.т.д.)

Т.о. a+b=c a=c-b т.е. в векторных равенствах вектора можно переносить из одной части в другую со сменой знака

Определение: Вектор е длина которого равна 1 и имеющий такое же направление что и ае называется ортом

№22---------------------------------------------------------------------------

Определение базиса, координаты вектора в базисе. Теорема о разложении вектора по базису.

Выражения вида называются линейной комбинацией векторов . Числа - коэффициенты линейной комбинации векторов. Линейная комбинация векторов обладает следующими свойствами: 1) Если коллинеарны то любая их линейная комбинация с ними коллинеарна.

2) Если компланарны то любая их линейная комбинация с ними компланарна.

Определение: 1) Любые три некомпланарных вектора взятые в определенном порядке называются базисом в пространстве.

2) Базисом на плоскости называется любая упорядоченная пара не коллинеарных векторов на этой плоскости.

3) Базисом на прямой называется любой отличный от 0 вектор этой прямой.

Вектор базиса на плоскость < >0, а в пространстве никакие 2 вектора не являются коллинеарными.

Если вектор представлен как линейная комбинация некоторых векторов то говорят что этот вектор разложен по этим векторам.

Определение: Если базис в пространстве и то числа называются координатами вектора в базисе . Обозначение .

Теорема. (о разложении по базису): 1)Каждый вектор какой-нибудь прямой может быть разложен по базису на этой прямой.

2)Каждый векторнекоторой плоскости может быть разложен по базису на этой плоскости

3)Каждый вектор может быть разложен по базису в пространстве.

4)Координата вектора в каждой из трех случаев определяется однозначно

Доказательство: 1) Пусть - базис на прямой и . И пусть ( + если и – если . Ясно что . .

2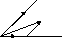) Пусть базис на плоскости. Перенесем начала векторов а, е₁ и е₂ в точку О. Через конец А вектора а проведем прямую .

Из рисунка видно что .

3) Пусть базис в пространстве. Вектор а – произвольный.

О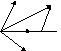тложим вектора от некоторой точки О. Дальше все рассуждения аналогичны пункту 2).

4) Докажем единственность разложения по базису. Методом от противного. Пусть вектор а можно разложить по базису двумя разными способами.

. Из (2) вычтем (1):

а это противоречит некомпланарности базисных векторов. Полученное противоречие доказывает единственность разложения векторов. (ч.т.д.)

Опираясь на свойства сложения и умножения векторов легко доказать следующие свойства:1) При умножении вектора на число его координаты умножаются на это число.

2) При сложении векторов соответствующие координаты этих векторов складываются.

№23---------------------------------------------------------------------------