
- •Понятие числового поля и матрицы над полем р...
- •Доказать, что любая транспозиция меняет характер четности перестановки. Определение Определителя n-ого порядка.
- •Теорема о разложении определителя на сумму определителей и следствия из нее.
- •Теорема о разложении определителя по элементам строки(столбца) и следствия из неё.
- •Операции над матрицами и их свойства. Доказать одно из них.
- •Операция транспонирования матрицы и её свойства.
- •Определение обратной матрицы. Доказать что у каждой обратимой матрицы существует лишь одно обращение.
- •Блочные матрицы. Сложение и умножение блочных матриц. Теорема об определителе квазитреугольной матрицы.
- •Теорема о существовании обратной матрицы.
- •Ранг матрицы. Теорема о базисном миноре. Необходимое и достаточное условие равенства нулю определителя.
- •Понятие о линейной зависимости строк и столбцов матрицы. Теорема о ранге матрицы.
- •Метод элементарных преобразований. (Метод Гаусса)
- •Системы линейных уравнений. Критерий совместности и критерий определенности.
- •Решение совместной системы линейных уравнений.
- •Необходимое и достаточное условие для того,чтобы ослу имела ненулевое решение.
- •Однородные системы линейных уравнений. Теорема о существовании фундаментальной системы решений.
- •Теорема о связи между решениями неоднородных и соответствующих однородных систем.
- •2) Разность двух произвольных решений неоднородной системы двух уравнений является решением соответствующей ослу.
- •Линейные операции над векторами и их свойства. Доказать одно из них.
- •Cвойства линейных операций над векторами
- •Теорема о существовании и единственности разности двух векторов.
- •Определение базиса, координаты вектора в базисе. Теорема о разложении вектора по базису.
- •Линейная зависимость векторов. Свойства понятия линейной зависимости, доказать одно из них.
- •Декартовы системы координат в пространстве, на плоскости и на прямой. Теорема о линейной комбинации векторов и следствия из нее.
- •Определение смешанного произведения векторов. Теоремы, выясняющие геометрический смысл смешанного произведения.
- •2. Если линия на плоскости в некоторой дск может быть задана уравнением вида (2) то и в любой другой дск она может быть задана уравнением того же вида имеющим туже степень.
- •Параметрические уравнения прямой и плоскости.
- •Переход от общих уравнений плоскости и прямой на плоскости к их параметрическим уравнениям. Геометрический смысл коэффициентов а,в,с (а,в) в общем уравнении плоскости(прямой на плоскости).
- •Исключение параметра из параметрических уравнений на плоскости( в пространстве), канонические уравнения прямой.
- •Векторные уравнения плоскости и прямой. Уравнение плоскости, проходящей через точку параллельно заданному вектору(в п.Д.С.К.).
- •Расстояние между непараллельными прямыми. Вычисление углов: между двумя прямыми, между прямой и плоскостью, между двумя плоскостями
- •Квп. Вывод канонического уравнения гиперболы. Асимптоты гиперболы.
- •Квп. Вывод канонического уравнения параболы.
- •2. Поворот
- •Поверхности второго порядка и их классификация. Основная теорема о пвп. Поверхности вращения.
- •Гиперболический цилиндр:
- •Основная теорема о пвп(без доказательства).Поверхности вращения.
Однородные системы линейных уравнений. Теорема о существовании фундаментальной системы решений.
Определение:
Линейно-независимая
система решений
![]() ОСЛУ
называется фундаментальной если каждое
решение ОСЛУ является комбинацией этих
решений.( Совокупность max
числа линейно-независимых решений
называется фундаментальной системой
решений).
ОСЛУ
называется фундаментальной если каждое
решение ОСЛУ является комбинацией этих
решений.( Совокупность max
числа линейно-независимых решений
называется фундаментальной системой
решений).
Теорема:
Если
![]() то ОСЛУ обладает ФСР.
то ОСЛУ обладает ФСР.
Доказательство:
Пусть
![]() и пусть для определенности минор Mr≠0
расположен в левом верхнем углу матрицы
А. Перенесем слагаемые содержащие
свободные неизвестные xr+1…xn
в правую
часть уравнения получим систему:
и пусть для определенности минор Mr≠0
расположен в левом верхнем углу матрицы
А. Перенесем слагаемые содержащие
свободные неизвестные xr+1…xn
в правую
часть уравнения получим систему:
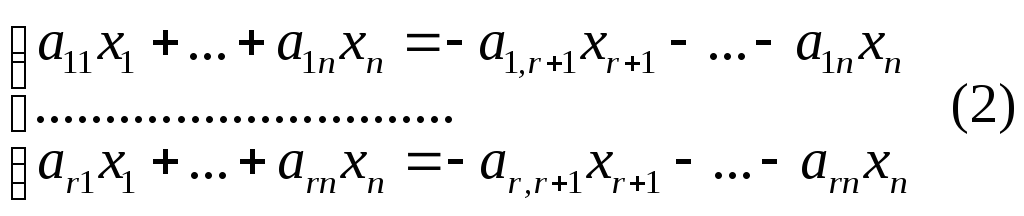 .
.
Придавая
свободным неизвестным значения
![]() мы из системы (2) получим
мы из системы (2) получим
![]() .
Это дает нам строку-решение
.
Это дает нам строку-решение
![]() .
Затем придавая свободным неизвестным
значения (0,1,0…0) получим
.
Затем придавая свободным неизвестным
значения (0,1,0…0) получим
![]() .
Это дает нам строку-решение
.
Это дает нам строку-решение
![]() и т.д. Продолжая этот процесс мы найдем
всего k=n-r
решений:
и т.д. Продолжая этот процесс мы найдем
всего k=n-r
решений:
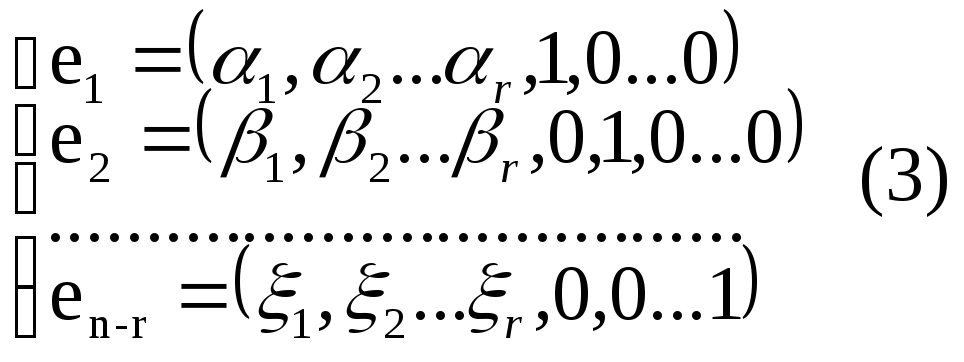 .
Эти n-r
решений независимы т.к. ранг образованной
ими матрицы имеет ранг n-r
решений.
.
Эти n-r
решений независимы т.к. ранг образованной
ими матрицы имеет ранг n-r
решений.
Покажем теперь что решения е1,е2… еn-r образуют ФСР. Согласно определению ФСР для этого надо показать что каждое решение ОСЛУ можно представить в виде линейной комбинации решений е1,е2…еn-r.
Пусть
![]() -
произвольное решение ОСЛУ. Рассмотрим
строку
-
произвольное решение ОСЛУ. Рассмотрим
строку
![]() .
Легко видеть что все элементы стоящие
на последних n-r
местах этой строки е0
будут равны 0, т.е.
.
Легко видеть что все элементы стоящие
на последних n-r
местах этой строки е0
будут равны 0, т.е.
![]() .
Т.к. е0 линейная
комбинация решений то строка е0
сама будет
решением ОСЛУ. А т.к. значение всех
свободных неизвестных в строке е0=0
то из однородности в этом случае системы
(2) определитель которой отличен от 0,
получаем что и значение всех неизвестных
в е0=0,
т.е. е0
есть 0 строка. Отсюда следует что
.
Т.к. е0 линейная
комбинация решений то строка е0
сама будет
решением ОСЛУ. А т.к. значение всех
свободных неизвестных в строке е0=0
то из однородности в этом случае системы
(2) определитель которой отличен от 0,
получаем что и значение всех неизвестных
в е0=0,
т.е. е0
есть 0 строка. Отсюда следует что
![]() (ч.т.д.)
(ч.т.д.)
Таким
образом можно сказать что общее решение
ОСЛУ имеет вид
![]() где е1,е2…еn-r
- ФСР, а
С1,С2…Cn-r
– произвольные числа.
где е1,е2…еn-r
- ФСР, а
С1,С2…Cn-r
– произвольные числа.
№19-дописать-------------------------------------------------------------
Теорема о связи между решениями неоднородных и соответствующих однородных систем.
Важно
отметить: Общее решение неоднородной
СЛУ равно сумме общего решения
соответствующей ОСЛУ и произвольного
но фиксированного решения СЛУ. Отсюда
следует что если е1,е2…еn-r
- ФСР (ОСЛУ)
и е0
- произвольное фиксированное решение
СЛУ то общее решение СЛУ имеет вид
![]() ,
где С1,С2…Cn-r
– произвольные числа.
,
где С1,С2…Cn-r
– произвольные числа.
Сформулированное утверждение следует из следующих очевидных утверждений : 1) Сумма любого решения неоднородной СЛУ и соответствующей ей ОСЛУ является решением неоднородной СЛУ.
2) Разность двух произвольных решений неоднородной системы двух уравнений является решением соответствующей ослу.
№20---------------------------------------------------------------------------
Линейные операции над векторами и их свойства. Доказать одно из них.
Определение: вектор - это направленный отрезок.
Будем
обозначать вектор AB . А - начало вектора,
В - конец вектора.![]() -
означает длина вектора (символ
модуля).Вектор называется нулевым,
если его начало и конец совпадают.
-
означает длина вектора (символ
модуля).Вектор называется нулевым,
если его начало и конец совпадают.
Определение: Два вектора называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях.
Определение: Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Определение: Пусть вектор AB и вектор A1B1 коллинеарны и пусть плоскость π пересекает прямые на которых они лежат. Плоскость π разбивает все пространство на два полупространство. Если перемещаясь по прямым в направление векторов AB и A1B1 мы попадем в одно полупространство(разные) то векторы AB и A1B1 называются одинаковонаправл. (противоположнонаправленными).
Определение: Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление. Два нулевых вектора считаются равными.
Из
определения равенства векторов следует,
что мы не различаем двух равных векторов,
имеющих разные точки приложения. Иными
словами, точка приложения вектора
![]() может быть произвольной. В соответствии
с этим векторы в геометрии называются
свободными.
может быть произвольной. В соответствии
с этим векторы в геометрии называются
свободными.
Элементы множества могут находиться в некоторых отношениях между собой. Отношения между парами объектов называются бинарными (двойными). Примером бинарных отношений является равенство. Отношение равенства между векторами обладает следующими свойствами :
1)
![]() - рефлексивность.
- рефлексивность.
2)
![]() - симметричность.
- симметричность.
3)
Если
![]() ,
,![]() то
то
![]() - транзитивность.
- транзитивность.
Бинарное отношение которое рефлексивно симметрично и транзитивно называется соотношением эквивалентности, таким образом отношение равенства векторов является отношением эквивалентности.
Линейными называются операции сложения и умножения вектора на число.
Сложение:
Суммой
![]() двух векторов
двух векторов
![]() называется
вектор, идущий из начала вектора
называется
вектор, идущий из начала вектора
![]() в конец вектора
в конец вектора
![]() при условии, что начало
при условии, что начало
![]() приложено к концу вектора
приложено к концу вектора
![]() .
.
Правило построения суммы 2-х векторов называется правилом треугольника:
![]() a,b-вектора
a,b-вектора
Правило
параллелограмма:
От точки А
отложим
![]() и
и
![]() ,
построим параллелограмм, тогда вектор
диагональ с началом в точке А является
суммой
,
построим параллелограмм, тогда вектор
диагональ с началом в точке А является
суммой
![]() и
и
![]() .
.
Определение: Произведение а на вещественное число называется b удовлетворяющее следующему условию:
1)
![]()
=
*
=
*![]()
2)
![]()
![]()
3)
![]()
![]() ,если
>0
,если
>0
4)
![]()
![]() ,если
<0
,если
<0
