Расстояние между непараллельными прямыми. Вычисление углов: между двумя прямыми, между прямой и плоскостью, между двумя плоскостями

Р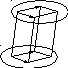асстояние между непараллельными прямыми. Пусть p непараллельна q. В этом случае существуют две такие параллельные плоскости P и Q что прямая p лежит в P а прямая q лежит в Q. Если уравнения прямых и то плоскость Р имеет начальную точку с радиус вектором и направляющими векторами и . А плоскость Q начальную точку с радиус вектором и теми же самыми направляющими векторами, так как Р параллельна Q.

Теорема: Прямые с уравнениями и пересекаются тогда и только тогда когда h=0.

В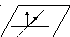ычисления углов: а) Угол между двумя прямыми это угол между направляющими векторами этих прямых.

б) Угол между прямой и плоскостью есть по определению угол ψ между прямой d и ее проекцией на плоскости. Получаем два угла ψ и π- ψ(тупой и острый). Каждый из этих углов заключен между 0 и π. В зависимости от выбора направляющего вектора прямой d и нормального вектора плоскости П имеем 4 угла попарно вертикальных. Обозначим через φ угол между любым вектором направляющим и любым нормальным вектором плоскости . Т.к. угол ψ заключен между 0 и π то его sin≥0, Причем

в) За угол между плоскостями принимают угол между любыми нормальными векторами к этим плоскостям. Это опять два угла – острый и тупой, дополняющие друг друга до π.

№42---------------------------------------------------------------------КВП. Вывод канонического уравнения эллипса. Параметрические уравнения эллипса.

О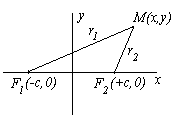пределение: Эллипсом называется множество точек на плоскости сумма расстояний от каждой из которых до двух заданных точек постоянна.

М – произвольная точка эллипса. О – середина F₁F₂. F₁F₂=2с. Сумма расстояний – 2a.Систему координат выберем таким образом чтобы Ох проходило через F_1, F₂ , а Оу делило пополам 2с.

F₁M+ F₂M=2a. - неудобное ур-е эллипса.

Преобразуем: ; 2a>2c, a>c,a²-c²=b²

- ур-е эллипса

Очевидно что каждая точка эллипса удовлетворяет этому уравнению. Но т.к. в процессе преобразований мы дважды возводили в квадрат обе части то необходимо проверить не получены ли лишние точки. Иначе говоря нужно проверить что каждая точка уравнения (4) принадлежит эллипсу. Предварительно сделаем несколько замечаний о форме линии, соответствующей уравнению (4). . Из уравнений видно что прямая симметрична относительно начала координат. С возрастанием от 0 до а, убывает от b до 0. Точки кривой лежат в прямоугольнике

Проверим теперь что каждая точка линии определяемая полученным уравнением принадлежит эллипсу. Для этого надо показать что если координаты точки М(х₀,у₀) удовлетворяют (4) то F₁M+ F₂M=2a.

Таким образом лишних точек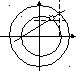 не появилось.

Числа и - большая и малая полуоси эллипса. F_1, F₂ – фокусы эллипса.

При получаем - уравнение окружности.

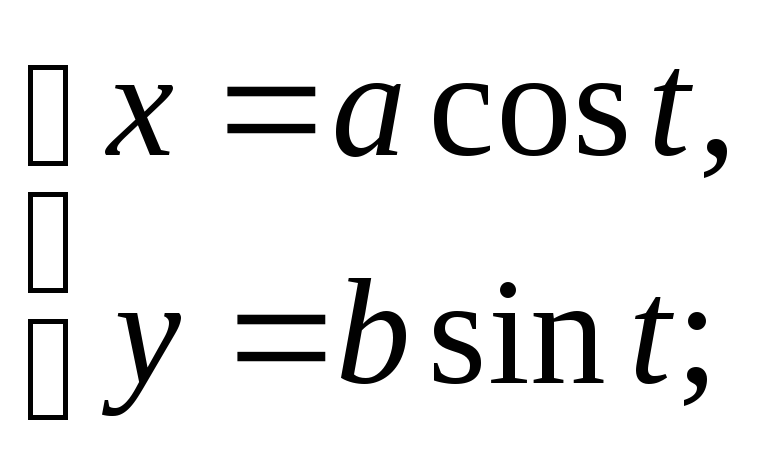Параметрические уравнения эллипса: Построим две окружности радиусом и с центром в начале координат. Из точки О проведем луч наклоненный к Ох под углом t. Проведем горизонтальную прямую через В и вертикальную через А. Изменяя t от 0 до 2 π точка М опишет эллипс. - парам-е уравнения эллипса. При а=b получим 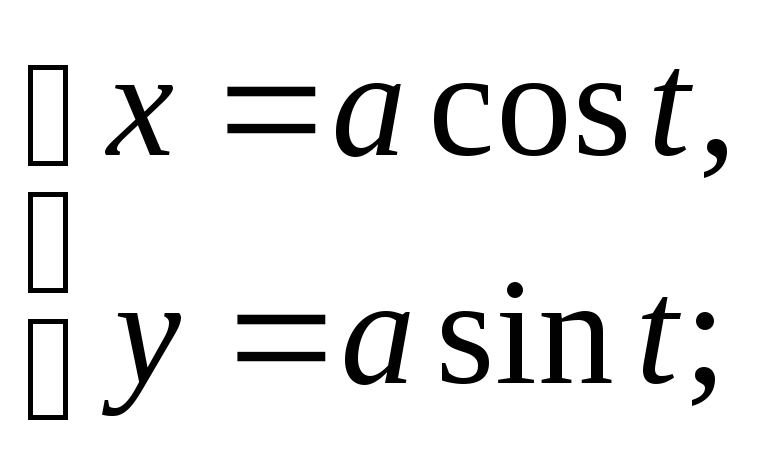- параметрические уравнения окружности.

№43---------------------------------------------------------------------------