Операция транспонирования матрицы и её свойства.

Определение: Матрица А’ получающаяся из матрицы А путем замены строк столбцами называется транспонированной по отношению к матрице А.

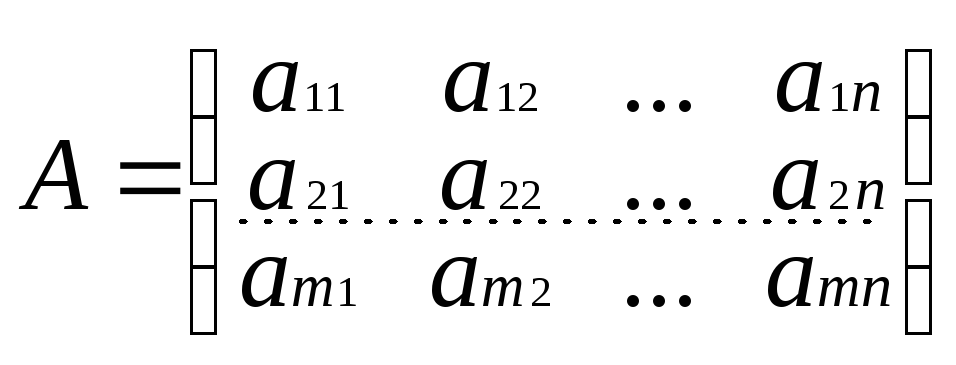
Справедливы следующие правила транспонирования матриц:

1. (αА+αВ)’=αA’ + αB’

2. (AB)’=B’A’

Идея доказательства показать что матрицы (AB)’ и B’A’ имеют одинаковую размерность и у них равны соответствующие элементы.

Определение: Если А – произвольная квадратная матрица и A=A’ (-A=A’), то матрица А называется симметрической или кососимметрической

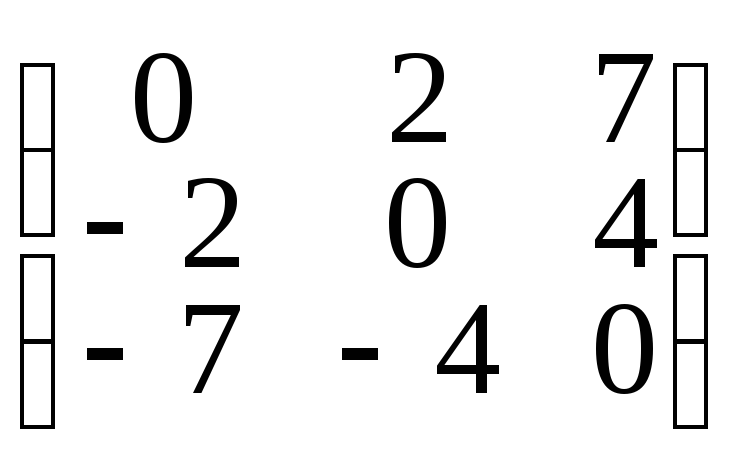
№4----------------------------------------------------------------------------

Определение обратной матрицы. Доказать что у каждой обратимой матрицы существует лишь одно обращение.

Определение: Квадратная матрица А называется обратимой если существует такая квадратная матрица Х что АХ=ХА=Е. (1)

Каждая матрица Х удовлетворяющая равенству (1) называется обратной матрице А или обращением матрицы А. Обратная матрица к матрице А обозначается А^-1

А А^-1= А^-1А=Е Отсюда следует что для матрицы А^-1 обратной будет (А^-1)^-1=А

Теорема: У каждой обратимой матрицы существует единственное обращение.

Доказательство: Предположим что у матрицы А существует наряду с Х еще одна обратная матрица У, т.е. АУ=Е. Тогда

(ХА)У=ЕУ=У ┐

Х(АУ)=ХЕ=Х ┘Следовательно Х=У. Т.е. у матрицы А существует единственное обращение.(ч.т.д.)

№5----------------------------------------------------------------------------

Определение обратной матрицы. Доказать что (АВС)^-1=С^-1В^-1А^-1.

Определение: Квадратная матрица А называется обратимой если существует такая квадратная матрица Х что АХ=ХА=Е. (1)

Каждая матрица Х удовлетворяющая равенству (1) называется обратной матрице А или обращением матрицы А. Обратная матрица к матрице А обозначается А^-1

А А^-1= А^-1А=Е Отсюда следует что для матрицы А^-1 обратной будет (А^-1)^-1=А (3)

Теорема: Если квадратные матрицы А, В, С одного и того же порядка обратимы, то их произведение тоже обратимо и (АВС)^-1=С^-1В^-1А^-1.

Доказательство: А(В(СС^-1)В^-1)А^-1=Е и С^-1(В^-1(А^-1А)В)С=Е (ч.т.д.)

Для любого натурального m по определению А^m=А*А*…*А – m-раз.

По определению А⁰=Е.

Определение: Для каждой обратимой матрицы А, А^-2=А^-1*А^-1; А^-3= А^-1*А^-1*А^-1 (4)

Из (3) и (4) следует что для каждой обратимой матрицы А и любых целых чисел р и q имеют место обычные правила действия со степенями:

А^рА^q =А^{р+ q}

(АВ)^р=А^рВ^р если АВ=ВА

(А^р)^q=А^р*q

№6----------------------------------------------------------------------------

Матрица,обратная к данной матрице. Доказать что в результате транспонирования обратимой матрицы получается снова обратимая матрица и (A’)^-1=(A^-1)’.

Определение: Квадратная матрица А называется обратимой если существует такая квадратная матрица Х что АХ=ХА=Е. (1)

Каждая матрица Х удовлетворяющая равенству (1) называется обратной матрице А или обращением матрицы А. Обратная матрица к матрице А обозначается А^-1

А А^-1= А^-1А=Е Отсюда следует что для матрицы А^-1 обратной будет (А^-1)^-1=А

Теорема: В результате транспонирования обратимой матрицы А получается снова обратимая матрица и (A’)^-1=(A^-1)’.

Доказательство: Применим правила транспонирования к соотношению АХ=ХА=Е:

(АХ)’=(ХА)’=Е’

А’Х’=Х’А’=Е

Из определения обратной матрицы следует что (A’)^-1= Х’=(A^-1)’(ч.т.д.)

№7----------------------------------------------------------------------------