Квп. Вывод канонического уравнения гиперболы. Асимптоты гиперболы.

Определение: Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная и не равная 0.

Выберем опять оси координат и начало координат посередине отрезка F₁F₂. Расстояние F₁F₂ равно 2с. А разность расстояний обозначим через 2а.

Из определения имеем: . 2а<2c, а<c

Имеем:

возведем в квадрат.

еще раз в квадрат. После простых преобразований получим:

Поделив обе части на получим: .

Как и в случае эллипса необходимо проверить что несмотря на двукратное возведение в квадрат мы не получим лишних точек. И следовательно уравнение (1) – уравнение гиперболы.

Предварительно отметим некоторые свойства линии определяемой уравнением (1). Из уравнения (1) следует что .

Линия (1) симметрична относительно осей координат и относительно начала координат. Видно что . Значит в полосе точек кривой нет. Следовательно кривая состоит из двух отдельных ветвей, одна из которых расположена в полуплоскости (правая ветвь), а вторая – в полуплоскости - (левая ветвь).

Пусть М(х₀,у₀) – произвольная точка линии, определяемая уравнением (1). . Если мы докажем что , то тем самым мы докажем что уравнение (1) является уравнением гиперболы.

далее в эту формулу подставляем у_0, раскрываем скобки, приводим подобные и учитывая что выделим под каждым корнем полные квадраты. В результате получим: . Пусть (для точек правой ветви), тогда .

При (для точек левой ветви) тогда .

Таким образом . Получаем что . Значит уравнение (1) – это уравнение гиперболы. Лишних точек не получилось.

Число а называется вещественной полуосью гиперболы, число b – мнимой полуосью. Точки пересечения гиперболы с ее осью симметрии называются вершинами гиперболы. Точки F₁ и F₂ фокусы гиперболы.

Отметим еще одну особенность формулы гиперболы. Рассмотрим вместе с гиперболой пару прямых . В первой четверти при одной и той же абсциссе ординаты точек гиперболы меньше соответствующих ординат соответствующих точек прямой, т.к. . , т.к. . Т.е. точки гиперболы при неограниченном увеличении абсцисс как угодно близко подходят к соответствующим точкам прямой . В силу симметрии точки гиперболы в других четвертях неограниченно приближаются к точкам прямых, когда .

Прямые - асимптоты гиперболы. Асимптоты гиперболы направлены по диагоналям прямоугольника со сторонами 2а и 2b, расположенного симметрично относительно осей симметрии гиперболы.

Если а=b то уравнение гиперболы принимает вид . Такая гипербола называется равнобочной.

№44---------------------------------------------------------------------------

Квп. Вывод канонического уравнения параболы.

Определение: Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а фиксированная прямая – директрисой параболы.

Для вывода уравнения построим:

Согласно определению:

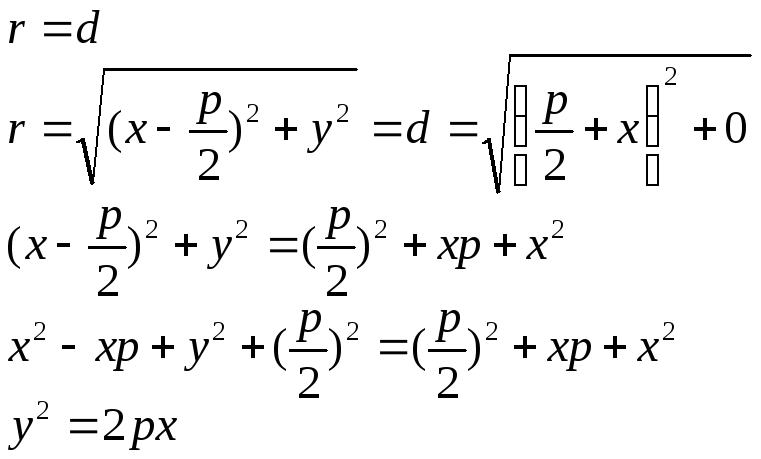
Так как у²>=0 то парабола лежит в правой полуплоскости. При х возрастающем от 0 до бесконечности . Парабола симметрична относительно Ох. Точка пересечения параболы со своей осью симметрии называется вершиной параболы.

№45--------дописать------------------------------------------------------

Эксцентриситет гиперболы. Пусть с- половина расстояния между фокусами гиперболы, а – действительная полуось гиперболы.

Определение: Эксцентриситетом гиперболы называется величина .

Учитывая связь между c,a,b получим: . Эксцентриситет гиперболы больше 1.

Замечание: Эксцентриситет гиперболы можно рассматривать как величину раствора угла между его асимптотами, т.к. , где φ – величина угла между асимптотами гиперболы.

№46--------дописать------------------------------------------------------

№47---------------------------------------------------------------------------

Кривые второго порядка и их классификация. Основная теорема о КВП (идея доказательства).

Существует 8 типов КВП:

1.эллипсы

2.гиперболы

3.параболы

Кривые 1,2,3 – канонические сечения. Если пересечь конус плоскостью параллельной оси конуса то получим гиперболу. Если плоскостью параллельной образующей то параболу. Все плоскости не проходят через вершину конуса. Если любой другой плоскостью то эллипс.

4.пара параллельных прямых y²+ a²=0, a0

5.пара пересекающихся прямых y²- k² x²=0

6.одна прямая y²=0

7.одна точка x²+ y²=0

8.пустое множество - пустая кривая (кр. без точек) x²+ y²+1=0 или x²+ 1=0

Теорема(основная теорема о КВП): Уравнение вида

a₁₁ x² + 2 a₁₂ x y + a₂₂ y² + 2 a₁ x + 2 a₂ y + a₀ = 0

может представлять только кривую одного из указанных восьми типов.

Идея доказательства состоит в том чтобы прейти к такой системе координат в которой уравнение КВП примет наиболее простой вид, когда тип кривой, которую оно представляет становится очевидным. Теорема доказывается с помощью поворота системы координат на такой угол при котором член с произведением координат исчезает. И с помощью параллельного переноса системы координат при котором исчезает или член с переменной х или член с переменной у.

Переход к новой системе координат: 1. Параллельный перенос