Теорема о существовании обратной матрицы.

Определение: Если матрица называется не невырожденной (неособенной). Если то матрица называется вырожденной (особенной).

Рассмотрим произвольную квадратную матрицу А. Из алгебраических дополнений элементов этой матрицы составим матрицу и транспонируем её. Получим матрицу С: матрица С называется присоединенной по отношению к матрице А. Вычислив произведение А*С и В*С получим Следовательно , таким образом если .

Таким образом из неособенности матрицы А следует существование А^-1. С другой стороны если А имеет А^-1 то матричное уравнение АХ=Е разрешимо. Следовательно и . Объединяя полученные результаты получим утверждение:

Теорема: У квадратной матрицы над полем Р существует обратная тогда и только тогда когда она не особенная. Если обратная матрица существует то она находится по формуле: , где С присоединенная матрица.

Замечание:

№10---------------------------------------------------------------------------

Ранг матрицы. Теорема о базисном миноре. Необходимое и достаточное условие равенства нулю определителя.

Определение: Минором k-того порядка матрицы А называется определитель k-того порядка с элементами, лежащими на пересечении любых k строк и любых k столбцов.

Определение: Рангом матрицы А называется наивысший порядок отличный от 0 миноров этой матрицы. Обозначается r(A). Ясно 0<=r(A)<=min(m,n). Таким образом если r(A)=r то среди миноров матрицы А есть минор r-го порядка отличны от 0, а все миноры r+1 порядка и выше равны 0.

Определение: Всякий отличный от 0 минор матрицы порядок которого равен рангу матрицы называется базисным минором этой матрицы. Ясно что матрица может иметь несколько базовых миноров. Столбцы и строки которые образуют базовые миноры называются базисными.

Теорема: В производной матрице А=(а_i)_m,n каждый столбец является линейной комбинацией базисных столбцов в которых расположен базисный минор(то же самое о строках).

Доказательство: Пусть r(A)=r. Выберем из матрицы один базисный минор. Для простоты предположим, что базовый минор расположен в левом верхнем углу матрицы, т.е. на первых r строках и первых r столбцах. Тогда базовый минор Mr будет иметь вид: 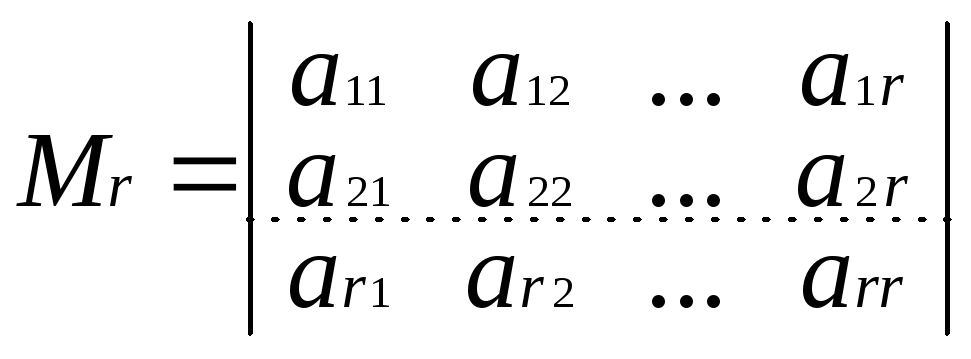. Нам нужно доказать что всякий столбец матрицы А является линейной комбинацией первых r столбцов этой матрицы, в которых расположен базисный минор, т.е. надо доказать что существуют числа λ_j такие, что для любого k-того столбца матрицы А имеет место равенство: где … .

Припишем к базисному минору какие-нибудь k-тый столбец и s-тую строку: 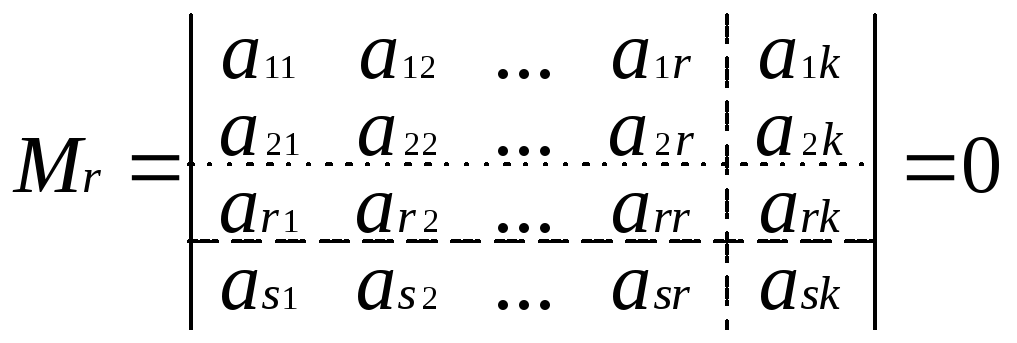т.к. если добавленная строка или

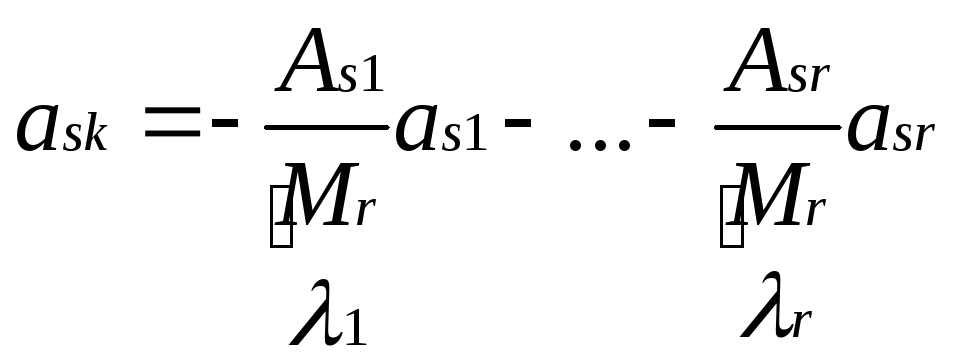
столбец входят в число базисных то определитель , как определитель с двумя одинаковыми строками(столбцами). Если добавлена строка(столбец) то согласно определению ранга матрицы. Разложим определитель по элементам нижней строки, получим: отсюда получаем: где λ₁… λ_r не зависят от номера S, т.к. А _Sj не зависят от элементов добавленной S-той строки. Равенство (1) и есть нужное нам равенство.(ч.т.д.)

Следствие: Если А квадратная матрица, а определитель A =0 ,то один из столбцов матрицы есть линейная комбинация оставшихся столбцов, а так же одна из строк является линейная комбинация оставшихся строк.

Доказательство: Если определитель матрицы A =0, то ранг этой матрицы <=n-1, n-порядок матрицы. Поэтому, по крайней мере одна строка или один столбец не входят в число базисных. Эта строка (столбец) линейно выраженная через строки (столбцы) в которой расположен базисный минор, а значит линейно выраженная через остальные строки (столбцы).

Для того чтобы [A] =0 необходимо и достаточно чтобы по крайней мере одна строка (столбец) являлись линейной комбинацией остальных её строк (столбцов).

№11---------------------------------------------------------------------------