Переход от общих уравнений плоскости и прямой на плоскости к их параметрическим уравнениям. Геометрический смысл коэффициентов а,в,с (а,в) в общем уравнении плоскости(прямой на плоскости).

Для этого перехода мы должны знать начальную точку и направляющие вектора. Пусть найдем начальную точку. Пусть 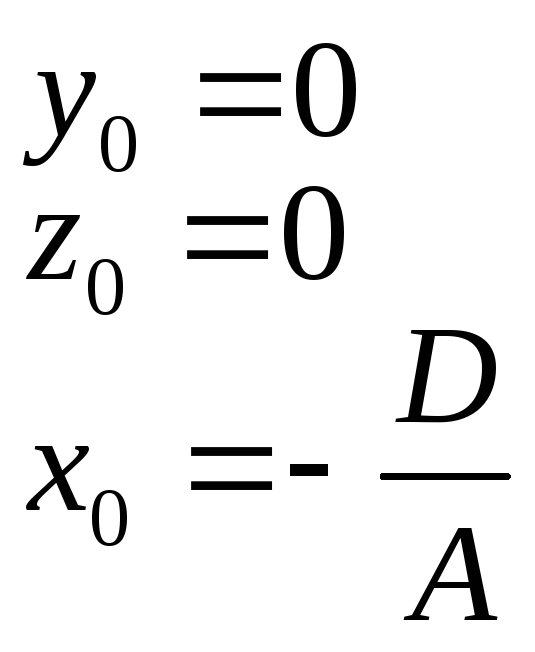. Для прямой начальная точка находится аналогично. Найдем теперь направляющие векторы. Пусть - уравнение прямой на плоскости и - начальная точка(*). . . Уравнение (*) равносильно уравнению (**). Если обозначить буквой М точку с координатами то вектор параллелен прямой тогда и только тогда когда точка М принадлежит прямой, т.е. когда верно равенство (**). Отсюда следует утверждение: Каждый ненулевой вектор с координатами (α₁, α₂) удовлетворяет условию: может быть принят за направляющий вектор прямой которая имеет своим уравнением уравнение в ОДСК. В частности вектор с координатами (-В,А) можно взять в качестве направляющего вектора прямой. Аналогично доказывается утверждение: Любых два неколлинеарных вектора координаты которых удовлетворяют условию могут быть приняты за направляющие векторы в плоскости, имеющую своим уравнением в ОДСК.

Геометрический смысл коэффициентов А,В,С(А,В) в общем уравнении плоскости (прямой на плоскости) в прямоугольной ДСК: Обозначим через - вектор с координатами (А,В). Левая часть уравнения (**) является скалярным произведением векторов и только в ПДСК. Поэтому из уравнения (**) следует что вектор с координатами (А,В) перпендикулярен вектору , если точка М принадлежит прямой. Таким образом вектор (А,В) перпендикулярен прямой, которая задается общим уравнением (*) в ПДСК и называется нормальным вектором прямой.

Аналогично вектор (А,В,С) является ортогональным плоскости которая задается общим уравнением в ПДСК и называется нормальным вектором в плоскости.

№34---------------------------------------------------------------------------

Исключение параметра из параметрических уравнений на плоскости( в пространстве), канонические уравнения прямой.

Рассмотрим на плоскости прямую заданную параметрическими уравнениями . а₁ и а₂ – координаты направляющего вектора. прямая не параллельна оси ОУ. -уравнение прямой решенное относительно ординаты. Его можно получить решая уравнение относительно у.

Определение : отношение координат направляющего вектора называется угловым коэффициентом прямой.

Таким образом справедливо утверждение: Если прямая не параллельна оси ОУ() то ее уравнение может быть записано в виде (4), где k – угловой коэффициент, а b – ордината пересечения прямой с осью ОУ.

Если ПДСК то из рисунка видно что Угол считается от оси абсцисс в направлении кратчайшего поворота от оси абсцисс к оси ординат.

Теорема: Если прямая параллельна оси ОУ(), то её уравнение имеет вид x=x₀, где x₀ – точка пересечения прямой с осью Ох.

Доказательство: Из (6) имеем (ч.т.д.)

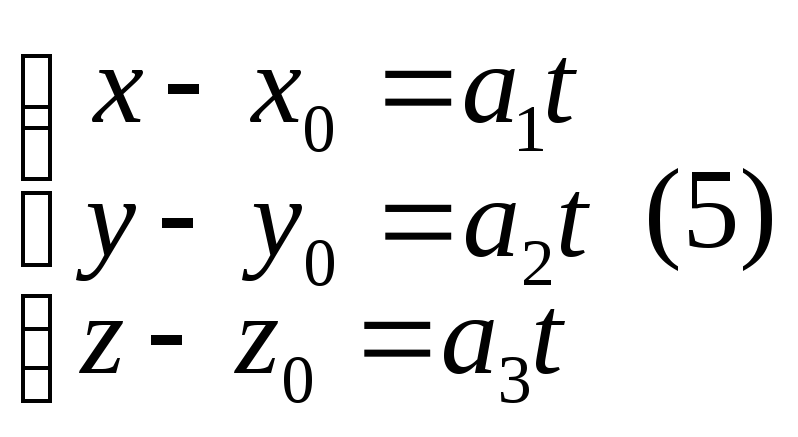
Исключим теперь параметр t из параметрических уравнений в пространстве. - координаты направляющего вектора прямой. Предположим сначала что все координаты направляющего вектора отличны от нуля, тогда т.е.

Замечание: Прямая в пространстве всегда может быть представлена как линия пересечения двух плоскостей. Значит она и должна задаваться системой из двух уравнений.

Пусть одна из координат равна 0. Пусть для определенности , тогда уравнения (5) будут иметь вид .

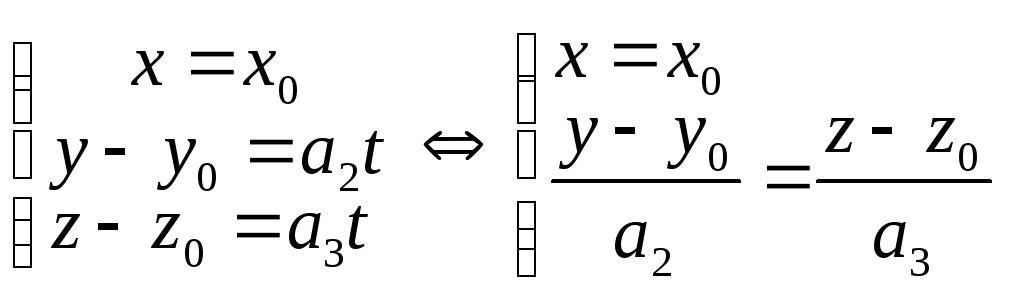Пусть и тогда . В этом случае прямая параллельна одной из координатных осей. В данном случае Oz.

Как правило пишут уравнение произвольной прямой в виде (2), уславливаясь считать что если равен 0 знаменатель, то числитель равен 0. Уравнения (2) называются каноническими уравнениями прямой. - направляющий вектор прямой.

№35---------------------------------------------------------------------------