Определение смешанного произведения векторов. Теоремы, выясняющие геометрический смысл смешанного произведения.

Пусть ,,- какие либо три вектора; - смешанное произведение векторов ,,. Следующая теорема позволяет выяснить геометрический смысл смешанного произведения.

Теорема1: Пусть ,, - три некомпланарных вектора. Отложим их от одной точки О. И построим на этих векторах параллелепипед. объему построенного параллелепипеда с + или – в зависимости от того какой является тройка векторов: правой(+) или левой(-).

Отложим от точки О . , где S – площадь параллелограмма. , где h – высота параллелепипеда, ,, - правая тройка значит +, левая значит - . (ч.т.д.)

Теорема 2: Для того чтобы три вектора ,,были компланарны( линейно зависимы) необходимо и достаточно чтобы (1)

Доказательство: Пусть ,,–компланарны, Если бы эти векторы были не компланарны, тогда на этих векторах можно построить параллелипипед. Объём которого равен V=а,b*c0- а это противоречит (1). Получили противоречие  ,,–компланарны.(ч.т.д.)

Из теорем 1 и 2 следует что т.к. модули и левой и правой частей равны объему одного и того же параллелепипеда и тройки , векторов имеют одинаковую ориентацию. Поэтому в дальнейшем смешанное произведение будем обозначать просто . Смешанное произведение меняет знак при перестановке двух сомножителей нечетное число раз, т.к. каждая перестановка двух сомножителей меняет ориентацию тройки векторов.

№29---------------------------------------------------------------------------

Выражение смешанного произведения трёх векторов через координаты перемножаемых векторовому в дальнейшем смешанное произведение будем обозначать просто евой(-).

0000000000000000000000000000000000000000000000000000

Теорема 3: Смешанное произведение векторов выражается через их координаты , , в произвольном базисе следующей формулой:

Доказательство:

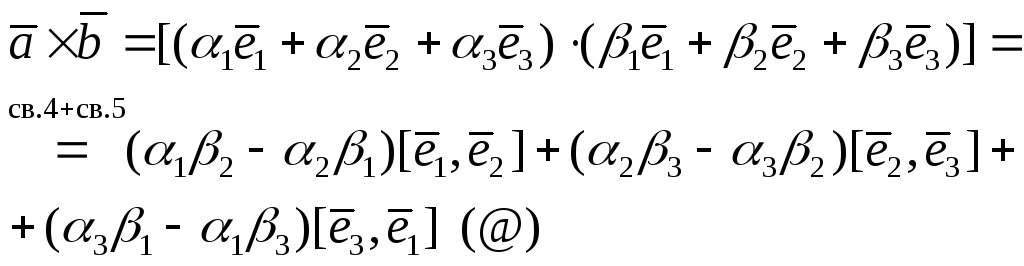
(ч.т.д.)

Если базис правый ортонормированный то и тогда

Необходимое и достаточное условие компланарности( линейной зависимости) трех векторов можно теперь записать в координатном виде

Двойное векторное произведение векторов. Определение и формула для вычисления( без доказательства).

Двойным векторным произведением называется произведение .

Можно доказать что для любых трех векторов ,,

№30---------------------------------------------------------------------------

Алгебраические линии и поверхности. Теоремы об инвариантности( неизменности) порядка.

Определение1: Алгебраической поверхностью называется множество точек, которое в какой-нибудь ДСК может быть задано уравнением вида . - неотрицательные целые числа. Наибольшее из этих чисел называется степенью уравнения или порядком поверхности.

Определение2: Алгебраической линией на плоскости называется множество точек которое в какой-нибудь ДСК на плоскости может быть определено уравнением . называются степенью уравнения или порядком линии.

Теорема об инвариантности( неизменности) порядка: 1. Если поверхность в некоторой ДСК может быть задана уравнением вида (1) то и в любой другой ДСК она может быть задана уравнением того же вида имеющим ту же степень.