Расчет соединений при несимметричном нагружении

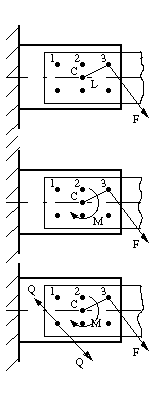Рис. 23.6

Если соединяемые элементы подвержены изгибу (несимметричное нагружение), то нагрузка между одиночными заклепочными соединениями распределяется неравномерно. В этом случае расчет групповых соединений сводится обычно к определению наиболее нагруженной заклепки и оценке её прочности. Рассмотрим соединение, содержащееnзаклепок одинакового диаметраd, под действием силыF (рис. 23.6, а). Примем для упрощения, что трение между соединяемыми деталями отсутствует, вся внешняя нагрузка передается через заклепки, деформации соединяемых де-талей малы по сравнению с деформацией стержней заклепок. При этих упрощениях можно полагать, что взаимный поворот соединяемых деталей произойдет вокруг точкиС– центра масс поперечных сечений стержней заклепок. Следовательно точкуСможно использовать в качестве центра приведения внешней силы. В результате приведения внецентренной силыFв точкеС задача расчета группового соединения сводится к определению наиболее нагруженной заклепки от действия центральной силыF и вращающего моментаM=Fl (рис.23.6,б).Если соединение подвержено действию нескольких силF₁, F₂,… F_n, то в результате приведения их к точкеС оно будет нагружено главным вектором и главным моментом от этих сил (рис.23.6, в).

При упругой деформации заклепок действие каждого силового фактора FиM можно рассматривать независимо. Тогда сила, приходящаяся на каждую заклепку отF, будет равна.

Момент М вызывает в каждой заклепке реактивную силу, направленную перпендикулярно к радиусу-вектору, проведенному из точкиС в центр сеченияi-ой заклепки. Эта сила пропорциональна перемещению сечения в результате деформации сдвига. Так как сдвиг сечений заклепок прямо пропорционален их расстояниямr₁, r₂… r_i,до центра масс, то можно записать:

, откуда

.

(23.1)

Если учесть что внешний момент М уравновешивается моментами от сил, действующих на заклепки, т. е.

то после подстановки уравнений (23.1) получим

или сила, действующая на i-ю заклепку

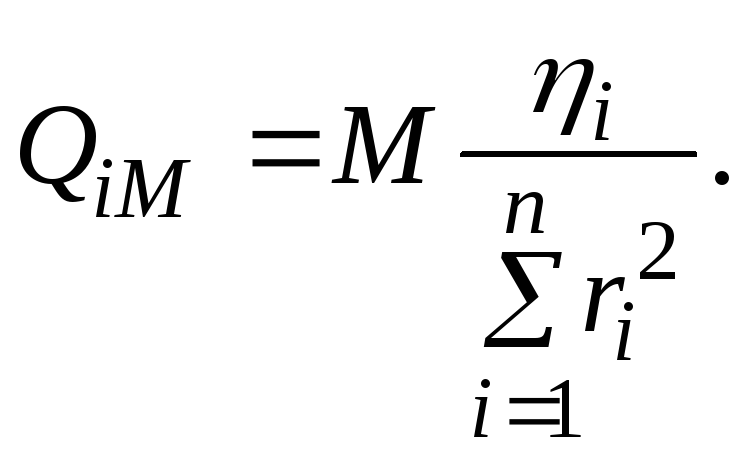
_{Сила, действующая на наиболее нагруженную заклепку}

_{а модуль этой силы}

_{гдеi - угол между векторами сил QF и QiM.}

_{По этой силе находится диаметр заклепки.}

Заключение

Данное учебное пособие предназначено для студентов заочного обучения и позволяет слушателям курса лекций «Детали машин» самостоятельно изучить многие вопросы, не затронутые в постановочных лекциях.

В пособии в полном объёме освещены разделы по изучению передач (зубчатых, червячных, ремённых), подшипников (скольжения и качения), соединений (резьбовых, шпоночных, шлицевых, сварных и заклёпочных), где приведены методики их проектирования и расчёта. Раздел по изучению осей и валов менее полно отражён в пособии, так как этому вопросу уделяется большое внимание в курсе «Сопротивление материалов».

К сожалению, ограниченный объём учебного пособия не позволяет осветить все разделы курса «Детали машин». Отсутствующие разделы курса, такие, например, как расчет и проектирование сложных (планетарных и дифференциальных) редукторов, вариаторов, шариково - винтовых передач, муфт, тормозных систем, зубчатых ремённых и цепных передач и т.д. при необходимости могут быть изучены студентами самостоятельно по учебникам и учебным пособиям [1-5].