Распределение нагрузки между телами качения

Принимаем следующие допущения:

1. радиальный зазор отсутствует;

2. кольца не деформируются.

3. контактные деформации описываются уравнениями Герца-Беляева.

По условию равновесия подшипника (рис. 14.7)

, (14.1)

г

Рис. 14.7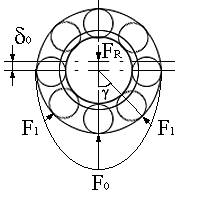

деF_r– радиальное усилие;

Рис. 14.8

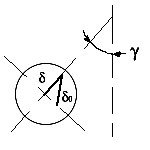
- угол между телами качения; z – число тел качения.

В уравнение (14.1) входят только те члены, для которых угол ngменьше 90⁰, так как верхняя половина подшипника не нагружена.

Под действием нагрузки F_r произойдет смещение внутреннего кольца подшипника на величинуd₀.При этом сдеформируются тела качения, причем величина деформации будет зависеть от положения шарика в нагруженной зоне (рис.14.8). Здесьd₀– смещение в вертикальной плоскости, тогда

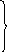
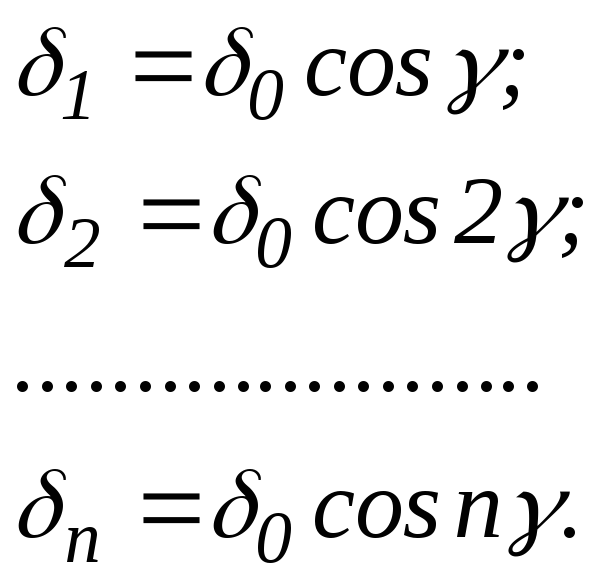(14.2)

С другой стороны по Герцу-Беляеву d =c F ^2/3, гдеc – const, (рис.14.9) тогда

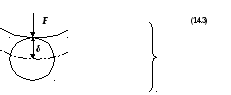Рис. 14.9

Решая совместно системы (14.2) и (14.3), получаем , но, тогда

или

. (14.4)

Подставляем выражение (14.4) в уравнение (14.1) и получаем

Рис. 14.10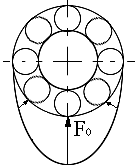

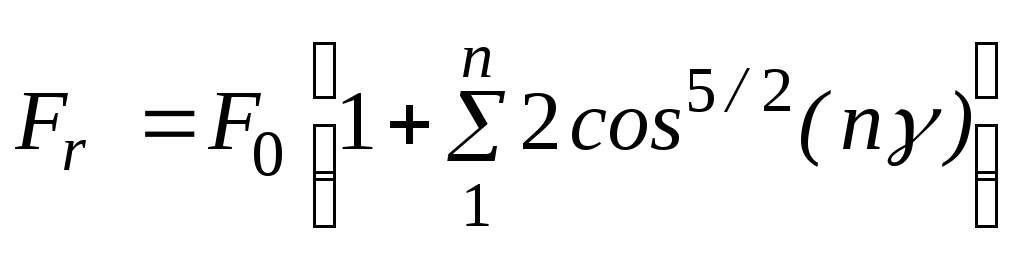откуда

.

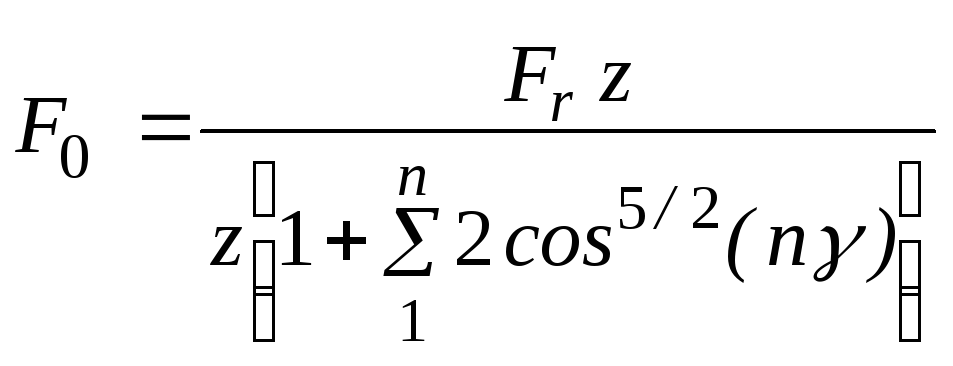или,

где.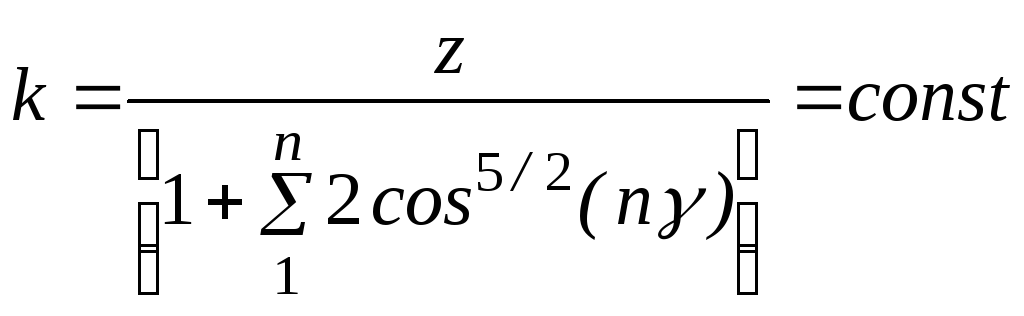

В практических расчетах принимают

- для шариковых; - для роликовых подшипников.

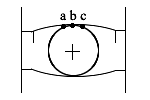
В итоге получаем распределение нагрузки по телам качения. Распределение нагрузки в значительной степени зависит от величины зазора в подшипнике и от точности геометрической формы его деталей (рис. 14.10). Поэтому к точности изготовления подшипника качения предъявляют весьма высокие требования.

Кинематика подшипника качения

Рис. 14.11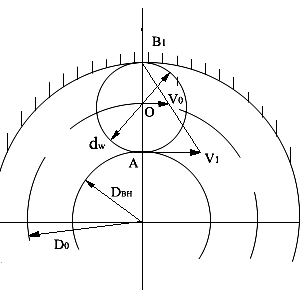

Рассмотрим случай, когда вращается внутреннее кольцо (рис 14.11). Здесь скорость точки А

.

Точка В– мгновенный центр скоростей вращающегося шарика. Скорость точек шара меняется линейно, таким образом

V₀=V₁/2.(14.5)

Так как V₀является и скоростью вращения сепаратора, тогда

, (14.6)

где n_c – частота вращения сепаратора. Из уравнений (14.5) и (14.6) получаемотсюда, так какD_вн=D₀-d_w

.

Число оборотов сепаратора меньше половины числа оборотов внутреннего кольца. Последняя формула позволяет отметить, что в точном выражении скорость сепаратора зависит от размеров шарика. Чем больше d_w, при постоянномD₀, тем меньшеn_c и наоборот.

При неточном изготовлении шариков крупные из них будут тормозить, а мелкие ускорять сепаратор. Между сепаратором и шариками могут возникнуть значительные давление и силы трения. С этим связан износ шариков и сепаратора, увеличение потерь на трение в подшипнике и случаи поломки сепаратора.

К

Рис. 14.12

онтакт шарика с кольцом осуществляется по некоторой дугеa-b-с(рис 14.12). Окружные скорости точекa иb при вращении шарика вокруг своей оси различны. Если допустить, что в точкеа(а-с– мгновенная ось вращения) нет скольжения, то оно будет в точкеb. Таким образом, в шариковых подшипниках наряду с трением качения наблюдается трение скольжения. Это создает дополнительный износ и потери в шариковых подшипниках. В роликовых подшипниках все точки контакта равноудалены от оси роликов. Здесь наблюдается чистое качение. Потери и износ в роликовых подшипниках меньше, чем в шариковых.

Лекция №15 Зависимость между грузоподъемностью и долговечностью подшипников качения

Рис. 15.1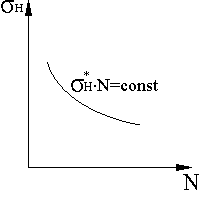

Подшипники качения не могут служить бесконечно долго, даже если они достаточно хорошо предохранены от износа и коррозии. Критерием работоспособности в этих случаях является усталостное выкрашивание поверхностных слоев. Кривая усталости для подшипников имеет вид гиперболы (рис 15.1) и описывается уравнением

,

где х=9– для шариковых подшипников;

х=10– для роликовых подшипников.

На основе больших экспериментальных данных установлена зависимость между эквивалентной динамической нагрузкой Р для подшипника и его динамической грузоподъемностьюС

, (15.1)

где L– долговечность подшипника в миллионах оборотов;n=3– для шарикоподшипников;n=10/3– для роликоподшипников.

Формула (15.1) справедлива при частоте вращения кольца n>10 мин^-1, но не превышающей предельной частоты вращения данного подшипника, приводимой в каталоге.При n=1…10 мин^-1 расчет подшипника производится для n=10 мин^-1.

Эквивалентной динамической нагрузкой P для радиальных и радиально-упорных подшипников качения называется такая постоянная радиальная нагрузка, которая при действии на подшипник с вращающимся внутренним кольцом и неподвижным наружным обеспечивает ту же долговечность, которую данный подшипник имеет при действительных условиях нагружения и вращения.

Динамическойгрузоподъемностью Срадиального и радиально-упорного подшипника качения называется такая постоянная радиальная нагрузка, которую группа идентичных подшипников при неподвижном наружном кольце сможет выдержать в течение расчетного срока службы, исчисляемого в1миллион оборотов внутреннего кольца. Она выбирается по каталогу.

При расчете подшипников принято за расчетный или гарантированный ресурс принимать такое число часов работы, которое выдерживает 90% всех подшипников, то есть10%подобранных по существующим нормам подшипников могут простоять в машине меньше требуемого срока. Однако средний ресурс в3…5раз превышает расчетный, а максимальный ещё в несколько раз превышает средний. Фактически выбраковывается значительно меньше подшипников, так как большинство подшипников в машинах недогружены.

Долговечность подшипника может быть определена в часах

,

где n – частота вращения внутреннего кольца.

При определении эквивалентной динамической нагрузки P учитывают тип подшипника, значения радиальной и осевой нагрузок на подшипник, характер действия этих нагрузок, температуру нагрева подшипника и какое кольцо вращается:

–для упорно-радиальных шарико- и роликоподшипников;

–для радиальных роликоподшипников;

–для упорных подшипников,

где F_r и F_a – постоянные по значению и направлению радиальная и осевая нагрузки на подшипник;

XиY–коэффициенты радиальной и осевой нагрузок, учитывающие их значение;

V – коэффициент вращения, учитывающий какое кольцо вращается – внутреннее или наружное:V=1– при вращении внутреннего кольца;

V=1,2– при вращении наружного кольца;

k_s -коэффициент безопасности, учитывающий характер нагрузки на подшипник;

k_T – температурный коэффициент, учитывающий рабочую температуру подшипника, если она превышает100⁰ С.

Из-за радиального зазора в подшипнике при отсутствии осевой нагрузки имеет место повышенная неравномерность нагружения тел качения. С увеличением осевой нагрузки, при постоянной радиальной, происходит выборка зазора и нагрузка на тела качения распределяется более равномерно. До некоторого значения - это компенсирует увеличение общей нагрузки на подшипнике с ростом осевой нагрузкиF_a (значения e – коэффициента осевого нагружения приведены в каталоге). В этом случае осевая нагрузка не снижает долговечность подшипника и расчет ведут на действие как бы одной радиальной нагрузки, то есть принимают Х=1 и Y=0. Если, то значенияX и Y выбирают по каталогу.

При установке вала на двух радиальных или радиально-упорных подшипниках нерегулируемых типов внешнюю осевую нагрузку воспринимает один из них, причем в том направлении, в котором он ограничивает осевое перемещение вала. При определении осевых нагрузок на радиально-упорные подшипники регулируемых типов следует учитывать осевую силу S, возникающую под действием радиальной нагрузки из-за наклона контактных линий,

которая представляет собой минимальную осевую силу, действующую на радиально-упорный регулируемый подшипник при заданной радиальной нагрузке.Для нормальной работы подшипника должно выполняться условие

F_a³S,

где S=eF_r– для шарикоподшипников;S=0,83eF_r– для роликоподшипников.

Таким образом, расчетная осевая нагрузка на подшипник складывается из внешней нагрузки на вал и осевой составляющей от другого радиально-упорного подшипника на вал.

Рассмотрим схематично вал, нагруженный радиальной силой F_rи осевой нагрузкойF_А(рис. 15.2). Условие равновесия вала

_, (15.2).

гдеF_a1 и F_a2 – осевые реакции на подшипниках

Дополнительные условия и.

Для нахождения решения в одной из опор осевая реакция принимается равной минимальной, то есть F_a=S.

Задаемся F_a1=S₁, тогда из (15.2) или. Осевая сила найдена правильно, если. Для случая, когда, следует принятьF_a2=S₂, тогдаи.

Причем условие будет обязательно выполнено.