Понятие об эквивалентных колесах и определение их размеров

В косозубом цилиндрическом колесе прочность зуба определяется его формой и размерами в нормальном сечении. Форма зуба в нормальном сечении n-n (рис. 7.8) соответствует форме зуба условного прямозубого колеса с модулем m_n и диаметром d_v=2r_v, где r_v – радиус кривизны эллипса в точкеР.

Р

Рис. 7.8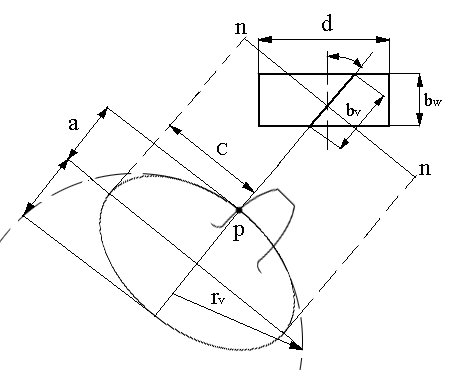

азмеры полуосей эллипса определяются в видеи.

Известно, что для эллипса, тогда диаметр эквивалентного колеса

.

С другой стороны диаметр эквивалентного колеса можно выразить как

где ;- эквивалентное число зубьев.

Так как , то, откуда.

Если принять ширину колеса , то такое колесо будет равнопрочным косозубому и называется эквивалентным колесом.

Расчет на контактную прочность

Рис. 7.9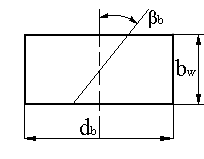

Согласно теории Герца - Беляева имеем

. (7.1)

Т.к. в зацеплении косозубой передачи всегда работает более одной пары зубьев, то нагрузка распространяется на несколько зубьев. Суммарная длина контактных линий определяется

(рис. 7.9), тогда.

Так как , а,то окончательно имеем

. (7.2)

Определим теперь приведенный радиус кривизны. Расчет делаем в полюсе зацепления. Индекс «t» означает, что мы рассматриваем параметры зацепления в плоскости перпендикулярной осям колес. Из рис 7.10,авидно, что мы имееми.

а б

Рис. 7.10

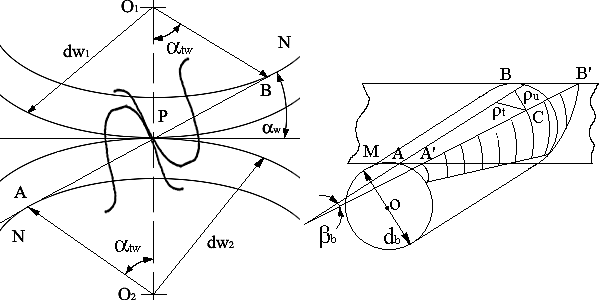
Рассмотрим основной цилиндр Ос диаметромd_b. Выделим плоскостьМ, касательную к основному цилиндру по образующейАВ. Проведем в плоскостиМпрямуюA'B'под углом_bк линииАВ. При обкатывании плоскостиМ без скольжения вокруг основного цилиндра прямаяA'B'опишет эвольвентный профиль косого зуба. Выделим на эвольвентном профиле некоторую точкуС (она лежит в полюсе зацепления).

Из рис. 7.10 следует, что

,

где _n – радиус кривизны эвольвенты в плоскости нормальной поверхности зуба, _t – радиус кривизна эвольвенты в плоскости перпендикулярной оси цилиндра.

,

тогда . (7.3)

Подставляя уравнения (7.2) и (7.3) в уравнение (7.1), получим выражение для контактных напряжений в виде

.

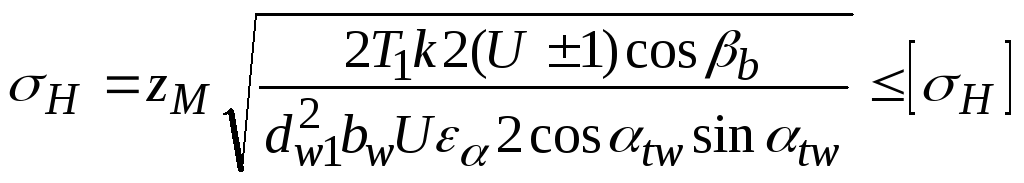Обозначим - коэффициент, учитывающий форму сопряженных поверхностей;- коэффициент, учитывающий влияние торцевого перекрытия.

Использовав последние обозначения, окончательно получим выражение

.

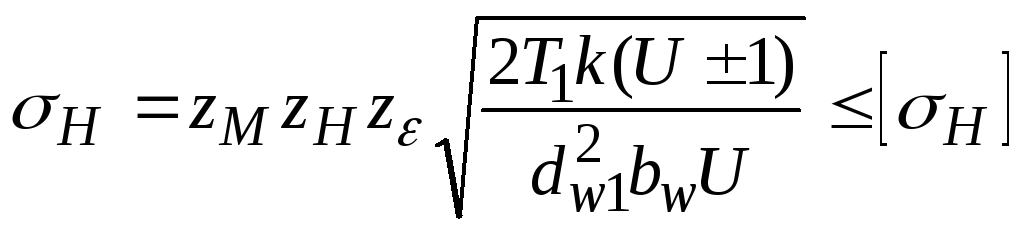Эта формула отличается от формулы проверочного расчета высокоточных прямозубых колес только значениями z_Hиz_,поэтому обозначим ихz_Hk иz_k.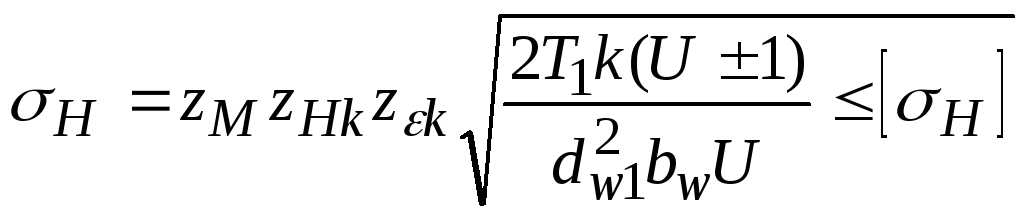

По аналогии, учитывая, что и, получим

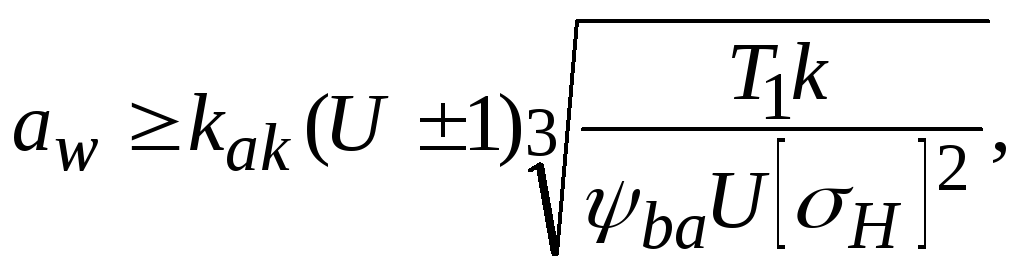
где

Это формула проектировочного расчета.

Расчет на изгибную прочность

В качестве исходной формулы возьмем формулу для прямозубого колеса.

Расчет выполняем для эквивалентного колеса, у которого

m_v=m_n, ,.

Для эквивалентного колеса окружным усилием будет являться усилие

.

Условие прочности для изгибных напряжений в косозубом колесе запишется

.

Обозначим коэффициент, учитывающий перекрытие зубьев, и получим.

Рис. 7.11

Рассмотрим распределение нагрузки для прямого и косого зуба (рис. 7.11).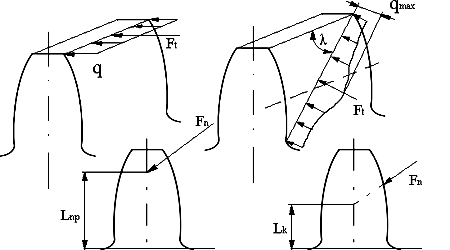

На боковой поверхности косого зуба линия контакта расположена под некоторым углом . Угол увеличивается с ростом значения. По линии контакта нагрузка распределяется неравномерно. Она имеет максимум на средней линии зуба, т.к. при зацеплении серединами зубьев они имеют максимальную суммарную жесткость. В косозубой передаче усилиеF_n (равнодействующая погонного усилияq) смещается к основанию зуба, поэтому. Это учитывается введением коэффициентаY_

, при 40;

, при >40.

Учитывая, что , получим формулу для проверочного расчёта

.

Отсюда, учитывая что, получим выражение для модуля.

Это формула проектировочного расчета.