sopromat2

После подстановки уравнения упругой линии (13) в граничное условие v (l) = 0 получаем уравнение совместности перемещений:

Из системы уравнений (11), (12), (14) определяем опорные реакции:

Строим эпюру поперечных сил Q в упругой стадии деформирования балки. Рассматривая левую часть балки (рис.3,б), составляем выражение для перерезывающей силы Q(z) и определяем координату ze, где Q(ze) = 0:

Эпюра перерезывающих (поперечных) сил Q показана на рис.3,в. Строим эпюру изгибающих моментов М(z) в упругой стадии

деформирования балки. Используя сумму моментов относительно центра сечения (рис.3,б), составляем выражение для M(z):

Изгибающий момент в сечении z = ze = 85 l:

Эпюра изгибающих моментов M(z) показана на рис.3,г. Допускаемую нагрузку qadm,el найдем из условия прочности по

допускаемым напряжениям:

где σy – предел текучести, ny – коэффициент запаса прочности по пределу текучести.

171

По эпюре изгибающих моментов M(z) на рис.3,г находим максимальный по абсолютному значению изгибающий момент max|M| = |M0| = 16ql2/128. Подставляя его в (16), получаем допускаемую нагрузку qadm,el в упругом расчете:

3.2. Отыскание предельной нагрузки способом упругих решений.

Изгибающий момент достигает экстремума в точке, где перерезывающая сила Q равна нулю. Координата ze сечения, где в пролете балки возникает Mmax в упругой стадии, определена в п.3.1.

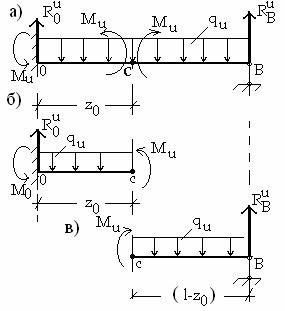
Пометим индексом "u" величины, относящиеся к предельному состоянию балки: предельный изгибающий момент – Mu, перерезывающую (поперечную) силу – Qu, опорные реакции – R0u , RuB ,

предельную нагрузку – qu. Величины R0u , RuB , Mu , qu , z0 являются

параметрами предельного состояния (z0 – расстояние от опоры O до пластического шарнира в пролете).

Для определения координаты z0 сечения, где образуется пластический шарнир в предельном состоянии балки, необходимо найти

Рассматривая равновесие всей балки можно составить 2 независимых уравнения (рис.4,а):

172

Отметим точкой c центр площади поперечного сечения z = z0, в котором возникает второй пластический шарнир; рассечем балку на две части и рассмотрим равновесие каждой из них при действии предельной нагрузки qu.

Левая часть балки ОС (рис.4,б):

∑ M(c) = 0 :− Mu + R0u z0−0,5quz02 − Mu = 0 , R0u z0 − 0,5quz02 = 2Mu ;(20)

Правая часть балки ВС (рис.4,в):

∑ M(c) = 0 :

Mu + 0,5qu(l−z0)2 − RuB(l− z0) = 0,RuB(l− z0) − 0,5qu(l− z0)2 = Mu . (21)

Исключив из уравнений (19), (20) опорную реакцию R0u , получим выражение для предельной нагрузки qu в виде:

Для определения координаты z0 составим выражение для Qu(z) и используем связь dM/dz = Q. Рассматриваем правую часть балки (рис.4,в):

Подставив значение RB по (23) и qu по (22) в уравнение Qu = 0 (25), получим квадратное уравнение для определения координаты z0:

173

Подставив значение z0 по (27) в уравнения (22), (23), получим значения предельной нагрузки qu и опорных реакций RO , RB :

3.3. Кинематический способ отыскания предельной нагрузки.

Балка может потерять геометрическую неизменяемость только по одной схеме, когда на опоре O и в пролете возникнут пластические шарниры. Установим их на опоре O и в сечении с координатой z = z0.

Так как перерезывающая (поперечная) сила в сечении z = z0 должна обратиться в ноль, рассмотрим равновесие звеньев ОС и ВС на рис.4,б,в:

Решение уравнения (32):

174

допускаемое значение нагрузки на балку в пластической стадии деформирования, вычисляемое по формуле (35), имеет значение

Отношение допускаемых нагрузок

qadm,pl = 75,65 = 2,28. qadm,el 33,15

4. Несущая способность двухпролетной балки.

Рассмотрим двухпролетную неразрезную балку постоянного поперечного сечения, нагруженную равномерно распределенной нагрузкой q1, q2 – рис.5. Осевой момент инерции – J, модуль упругости материала балки – Е. Соотношение между нагрузками q2 = aq1, а – число. Предел текучести материала балки – σy, коэффициент запаса по пределу текучести – ny. Найдем допускаемую нагрузку на балку расчетом по допускаемым напряжениям – qadm,el и по предельному равновесию – qadm,pl.

Рис.5. Двухпролетная неразрезная балка.

4.1. Упругий расчет двухпролетной балки. Вначале полагаем, что в любой точке балки напряжения не должны превышать величины σy / ny =

σadm : max|σ| ≤ σadm.

Построим эпюры поперечных сил и изгибающих моментов для балки на рис.5. На опорах возникают три вертикальные реакции: R0, RB, Rc.

Балка один раз статически неопределимая. Для раскрытия статической неопределимости используем метод начальных параметров (см. Приложение 2). Предварительно составляем уравнения равновесия:

176

Универсальное уравнение упругой линии на n-ом участке балки (метод начальных параметров):