§ 22.7. Теорема Умова —

Пойнтинга в комплексной формезаписи. Перед тем как записать теорему Умова — Пойнтинга в комплексной форме, рассмотрим вопрос о полной мощности в цепи

переменного тока. Полная мощность S = UI = Р + jQ.

Пусть цепь переменного тока содержит последовательно соеди­ненные активные сопротивления R,. индуктивность L и емкость С. Тогда реактивная мощность

где U_c—напряжение на конденсаторе.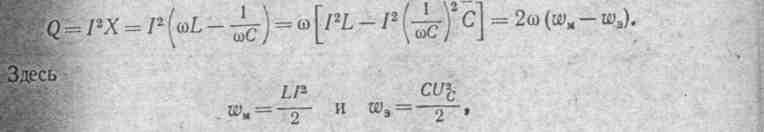

Таким образом, реактивная мощность Q равна разности между

магнитной v_м и электрической w_э энергиями цепи, умноженной на 2.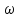

Подобно тому как в цепи переменного тока для вычисления полной

мощности S надо умножить комплекс напряжения U на сопряженный

комплекс тока I, вводится в употребление комплексный вектор Пойнтинга

Первое слагаемое правой части (2-2.13) представляет собой активную мощность, второе — реактивную. Таким образом, теорему Умова— Пойнтинга можно записать еще следующим образом:

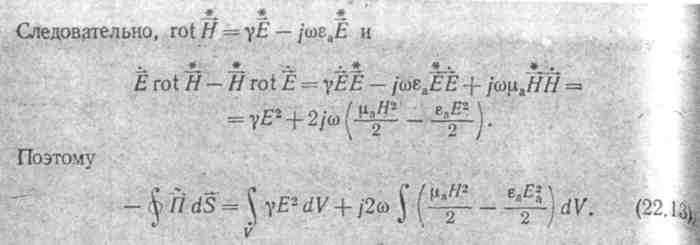
В таком виде ее часто используют для определения активного и внутреннего реактивного сопротивлений проводников на переменном токе (подробнее см. § 23.7).

§ 22.8. Некоторые замечания к § 22.1. Первое замечание. В уравнения Макс- велла входят параметры ε_а, γ, μ_а, характеризующие усредненные в пространственном и временном смысле свойства вещества. При низких частотах эти параметры представляют собой действительные (некомплексные) числа— такими и будем их считать в курсе ТОЭ. При высоких частотах в диэлектриках существенную роль на­чинают играть диэлектрическая вязкость и другие процессы.

В ферромагнитных веществах резко сказываются явления гистерезиса, маг- нитной вязкости и ряд других. В силу этих причин ε, γ, μ оказываются функциями частоты и комплексами .

Убедимся в том, что вязкостные процессы при поляризации диэлектриков с полярными молекулами приводят к тому, что ε становится комплексным числом.

Обозначим —напряженность поля, обусловленную приложенным к конден- сатору напряжением u; .например, для плоского, конденсатора с. расстоянием d между обкладками Еп = u./d; Е_Д — действующая на диполи.полярных молекул напряженность поля, вызывающая их поворот.

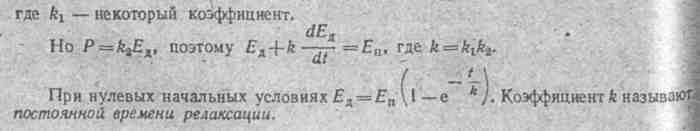
За счет вязкостных процессов при поляризации (повороте) полярных молекум E_Д< E_п на величину, пропорциональную скорости поляризации:

* Зависимость параметров веществ от частоты впервые была обнаружена русским ученым В. К. Аркадьевым в 1908—1911 гг. Физическое объяснение этим явлениям было дано им в 1913 г. в работе «Теория электромагнитного поля в ферромагнитном металле».

128

Первое слагаемое правой части находится в фазе с приложенным напряжением, второе на 90° его опережает. Тангенс угла потерь, несовершенного диэлектрика (см.

§3.9) tgα = ε^П+γ/ω/ε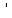Используя уравнение (16.34) § 16.8-для вязкостных процес­сов в ферромагнетиках, можно вывести аналогичные формулы и для.: комплексной магнитной проницаемости в предположении, что вихревые токи отсутствуют.

Заметим, что дифференциальное уравнение, описывающее процесс зарядки кон­денсатора с вязким диэлектриком через сопротивление R от источника постоянной; э. д. с, если учесть вязкостные процессы по уравнению (22.14), будет иметь вто­рой (не первый!) порядок.

Второе замечание. В § 22.2 рассматривалось первое уравнение Максвелла (22.1) В правой части этого уравнения записаны две плотности тока — проводимости 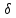и электрического смещения ε_а dE/dt. Но кроме токов проводимости и электрического смещения существует третий вид тока—ток переноса (это собирательное назва­ние).

Под током переноса понимают ток, природа которого отлична от природы тока проводимости и тока смещения, это, например, toк возникающий в электронной лампе вследствие явления термоэлектронной эмиссии. Плотность тока переноса равна объемной плотности переносимых зарядов ρ, умноженной на скорость их переноса ν. _

Если ток переноса создается движением со скоростью v₊ положительно заря­женных частиц с объемной плотностью р₊ и движущихся со скоростью v_ отрицательно заряженных частиц с объемной плотностью р., то плотность тока переноса равна ρ₊ν₊+ р_- v_- Ток переноса, так же как и остальные виды токов, создает, магнитное поле.

С учетом тока переноса первое уравнение Максвелла записывают следующим образом:

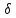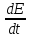rot H= +ε_а + pv.

¹/₂5 Зак. 1730 129

Для тех задач, которые рассматриваются в ч. III учебника, ток переноса отсутствует, поэтому первое уравнение Максвеллами взято в форме (22.1).

Третье замечание. При чрезвычайно высоких частотах, когда длина электромагнитной волны становится соизмеримой с линейными размерами, характеризующими молекулярную структуру самого вещества, вещество уже нельзя рассматриватькак континуум. В этом случае уравнения Максвелла должны быть заменены уравнениями квантовой теории поля..

Четвертое замечание. В Курсе ТОЭ в основном рассматривают поля в изотропных линейных средах. В них вектор В = μ_аH совпадает по направлению с вектором H, вектор D = ε_а E совпадает по направлению с E и вектор 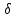=γЕ с Е. В изотропных средах μ, ε и γ представляют собой некоторые постоянные числа не зависящие от величины H или E (но зависящие от частоты). Если проекции вектора Bна оси х, у,z обозначить В_х, В_у, В_z, а проекции H — через Н_х, Нγ, Н_z, то для изотропных сред В_х= μ_аH_x, В_у= μ_а H_γ,B_z= μ_аH_z. Аналогично, D_х= ε_аЕ_х;D_y= ε_аE_y;D_z= ε_аE_zи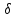_х= γЕ_хи т. д. В анизотропных средах В = μ_аH не совпадает по направлению с Н, D с Е, 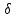с Е. Любая проекция В, D и 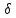зависит не толькоот одноименной проекции H или Е, но и от разноименныхи.проекций. Так, В_х зависит не только от Н_х, но и от H_y Н_z; B_x = μ_xx H_x + μ_ху Н_у + μ_xz H_z; аналогично, В_y = μ_ухН_х + μ_уу Н_у +μ _yzН_z, где μ_xx , μ_ух, , μ_xz — составляющие тензора магнитнойпроницаемости μ_а

Подобные выражения существуют и для тензоров ε_аи γ.

§ 22.9. Основные положения электродинамики движущихся сред (основы реля­тивистской электродинамики). Положим, что имеются две системы отсчета коорди­нат и времени. Одна система неподвижна, имеет начало в точке О, координаты про­извольной точки в ней х, у,z и время t (система О): Другая система отсчета связана с движущейся по отношению к предыдущей системе отсчета средой, имеет начало_: в точке O₁, a координаты той же точки в ней x_1; у₁, z₁ и время t (система О_1). Допустим , что в момент времени t= 0 обе системы координат совпадают и что скорость движения среды v направлена по оси х. Тогда в соответствии с теорией относительности можно записать преобразования Лоренца, связывающие координаты и время в обеих системах отсчета:

где с — скорость света, β= v/с.

Обозначим напряженность электрического поля и магнитную индукцию в произвольной точке, которые бы измерил наблюдатель, неподвижный по отношению к системе О, соответственно какЕ и В. Физически E означает силу, действующую наединичный покоящийся заряд в системе 0, а В — силу, действующую на единичный элемент тока, неподвижный в системеО: Е =iE_x + jE_y+kЕ_z; В =iB_x+ jBy+kB_zНапряженность электрического поля и магнитную индукцию, которые измерил бы наблюдатель, неподвижный по отношению к системе О₁ (т. е. движущийся со средой со скоростьюv), обозначим E₁иВ₁. ФизическиЕ₁ означает силу, действующуюна единичный покоящийся в системе О₁ заряд; B₁- силу, действующую на единичный элемент тока, покоящийся в движущейся среде: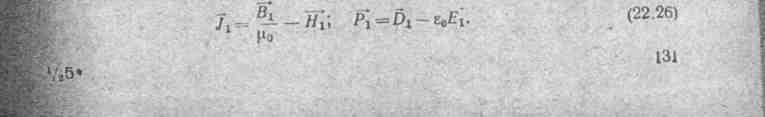

E₁=iE_x1+jE_y1 + kЕ_z1; B₁= iB_x1 + jBy₁ +kB_z1

Перейдем от уравнений Максвелла для неподвижных сред к уравнениям Максвелла для движущихся сред. С этой целью частные производные пох, у,z при взя-

130

Обратим внимание еще раз на то, что в системе О₁ операции дифференциривания при взятии ротора и дивергенции производятся по координатам х₁, y₁,z ₁. В системеO₁, для которой среда неподвижна, выполняется условие непрерывности тангенциальной составляющей напряженности E_tl, тангенциальной составляющей H_t1 и непрерывность нормальных составляющих .D_nlи В_n1. В системе О₁

Из уравнений (22.17) и (22.22) следует, что если в системе О магнитное поле отсутствует (В = 0), но имеется электрическое (Е 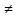0), то в системе О₁ имеется не только электрическое, но и магнитное поле. Из уравнений (22.19) и (22.21) заключаем, что если в системе О отсутствует электрическое поле (Е = 0), но есть магнитное (В 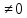), то в системе О₁ наблюдается не только магнитное, но и электрическое поле. Плотность тока 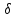₁ в системе О₁ создается не только током проводимости 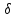, но и током переноса αvρ [см. уравнение (22.18)].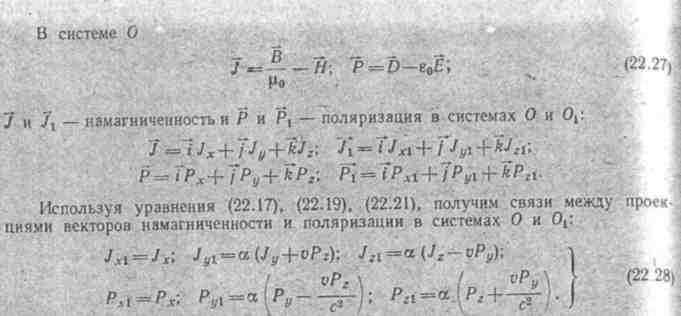

В соответствий с уравнением:(22.25) перемещение; тока с плотностью _х парал­лельно: самому себе с системой О₁ наблюдатель в системе О воспринимает как воз­никновение объёмного заряда v/с2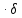_х,, дополнительного к объемной плотности заряда p₁. В соответствии с уравнением (22.28) движение поляризованной среды со скоростью v воспринимается в системе О как появление дополнительной намагниченности, а движение намагниченной среды со скоростью v воспринимается в системе О как возникновение дополнительной поляризации.

Для поля, связанного с системами О и О₁ имеют место следующие инварианты:

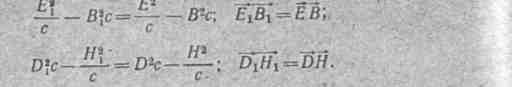
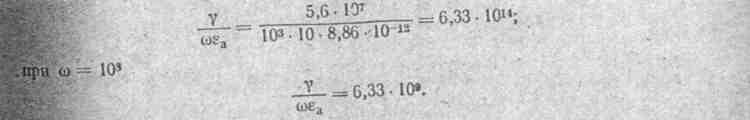
Если скорость движения среды мала по сравнению со скоростью света, то (v²/ c²) 1 и α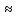 1, при этом преобразования Лоренца переходят в преобразования Галилея х₁= х — vt,y₁ = у, z₁ = z, t₁ = t, а связи между величинами в системах О и О₁, становятся такими:

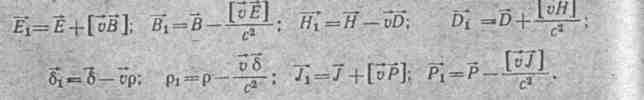
Вопросы, для самопроверки

1. Дайте определение переменного электромагнитного поля и запишите сово- купность уравнении Максвелла. 2. Покажите, что из первого уравнения Максвелла следует принцип непрерывности полного тока (или закон сохранения заряда), а из второго — принцип непрерывности магнитной индукции. 3. Чем объяснить, что во втором уравнении Максвелла, в отличие от первого, поставлен знак минус? 4. Ка­кие уравнения в интегральной форме соответствуют 1-му и 2-му уравнениям Макс­велла? 5. Прокомментируйте теорему Умова—Пойнтинга для мгновенных значе-

132

ний величин и для величин в комплексной форме записи. 6. Можно ли утверждать, что при постоянном токе электромагнитная энергия передается по проводам? 7. Поясните смысл преобразования, осуществляемого с помощью теоремы Остроградского Гаусса. 8. Чем объяснить, что показание вольтметра в переменном электромаг­нитном поле зависит от того, как расположены провода от вольтметра до объекта измерения. 9. Поясните, в силу каких причин ε, у и . Могут оказаться комплекс­ными числами. 10. Какие среды называют анизотропными? 11. Решите задачи 22.2; 22.9;22.11.

ГЛАВА ДВАДЦАТЬ ТРЕТЬЯ

БЕРЕМЕННОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ОДНОРОДНОЙ И ИЗОТРОПНОЙ ПРОВОДЯЩЕЙ СРЕДЕ