
- •Часть III
- •§ 19.2. Закон Кулона. Два точечных заряда qt и q2 в вакууме взаимодействуют друг с другом с силой f, прямо пропорциональной
- •§ 19.3. Напряженность и потенциал электростатического поля.
- •§19.6. Выражение напряженности в виде градиента потенциала.
- •§ 19.8. Выражение градиента потенциала в цилиндрической и сферической системах координат. В цилиндрической системе (обозначения см. На рис. 19.4, а):
- •10. Свободные и связанные заряды. Поляризация вещества.
- •§ 19.12. Вектор электрической индукции . Кроме векторов е и р в электротехнических расчетах используют еще вектор электрической индукции, или вектор электрического смещения d.
- •§ 19.18. Выражение div e в цилиндрической и сферической системах координат.
- •§ 19.20. Граничные условия. Под граничными условиями понимают условия, которым подчиняется поле на границах раздела сред с разными электрическими свойствами.
- •§ 19.21 Поле внутри проводящего тела в условиях электростатики.
- •§ 19.23. Условия на границе раздела двух диэлектриков. На границе раздела двух диэлектриков с различными диэлектрическим проницаемостями выполняются два следующих условия:
- •§ 19.25. Общая характеристика задач электростатики и методов их решения. В зависимости от того, что задано и что определяют, задачи электростатики можно подразделить на три типа.
- •§ 19.35. Емкостные коэффициенты. Вторая группа формул Максвелла. Решим систему (19.48) относительно зарядов, полагая потенциалы φ и коэффициенты α известными:
- •§19.36. Частичные емкости. Третья группа формул Максвелла.
- •§19.37, Поле точечного заряда, расположенного вблизи проводящей сферы.
- •§ 19.38. Поле заряженной оси, расположенной параллельно цилиндру. Рассмотрим две родственные задачи на изображение в диэлектрическом и проводящем цилиндрах.
- •§19.39. Шар в равномерном поле. Если в равномерное поле (направлено сверху вниз: вдоль оси — z), напряженность которого
- •§ 19.40, Проводящий шар в равномерном поле. Для определения
- •§ 19.43. Понятие о плоскопараллельном, плоскомеридианном и равномерном полях. В литературе можно встретить термины «плоскопараллельное поле», «плоскомеридианное поле» и «равномерное
- •§ 19.44. Графическое построение картины плоскопараллельного поля.
- •§ 19.47. Энергия поля системы заряженных тел. Энергия поля, образованного системой п заряженных тел, имеющих потенциалы φ1.... Φn и заряды q1…..Qn
- •§ 19.48. Метод средних потенциалов. Как уже говорилось в электростатическом поле, образованном системой заряженных проводящих тел, все точки поверх-
- •§ 19.49. О расчете электрических полей, создаваемых диэлектриками, сохраняющими остаточную поляризацию при снятии внешнего поля. Поле, которое создает
- •§ 20.3. Первый закон Кирхгофа в дифференциальной форме.
- •§ 20.4. Дифференциальная форма закона Джоуля — Ленца. В гл. 1
- •§ 20.8. Экспериментальное исследование полей. Если форма гра- ничных поверхностей (электродов) сложна, то аналитический расчет
- •§ 21.3. Дифференциальная форма закона полного тока. Соотношение (21.3) пригодно для контура любых размеров, в том числе и для весьма малого.
- •§ 21.7. Выражение проекций ротора в цилиндрической и сферической системах координат. Без вывода приведем выражение проекций
- •§ 21.14. Выражение магнитного потока через циркуляцию вектора-потенциала. Магнитный поток, пронизывающий какую-либо поверхность ,
- •§ 21.17. Задачи, расчета магнитных полей. Рассмотрим некоторые типы
- •§ 21.18. Общая характеристика методов расчета и исследования
- •§ 21.19. Опытное исследование картины магнитного поля. Опытноеисследование картины магнитного поля производят различными методами.
- •§ 21.21. Магнитное экранирование, Положим, что в равномерном магнитном поле напряженностью н0 надо заэкранировать некоторую область пространства, например цилиндрическую, так, чтобы напря-
- •§ 21.26. Магнитное поле намагниченной пленки (ленты). Магнитная пленка
- •§ 21.28. Выражение механической силы в виде производной от энергии маг нитного поля по координате. Положим, что в системе из п контуров с токами
- •§ 22.2. Первое уравнение Максвелла. Первое уравнениеМаксвела записывают следующим образом
- •§ 22.3. Уравнение непрерывности. Линии полного тока
- •§ 22.4. Второе уравнение Максвелла. Второе уравнение Максвелла
- •§ 22. 6 Теорема Умова - Пойнтинга для мгновенных значений.
- •§ 22.7. Теорема Умова —
- •§23.1. Уравнения Максаелла для проводящей среды. Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью у и магнитной проницаемостью μа.
- •§23.3. Распространение плоской электромагнитной. Волны в однодном проводящем полупространстве. Рассмотрим вопрос о распространении плоской электромагнитной волны в однородной
- •§ 23.7. Неравномерное распределение тока в прямоугольной шине, находящейся в паазу электрической машины. Расположим оси декартовой системы в соответствии
- •§ 23.10. Экранирование в переменном электромагнитном поле.
- •§ 24.2. Плоские волны в однородных и изотропных полупроводящих средах.
- •§ 24.3. Граничные условия на поверхности раздела двух полупроводящих сред
- •§ 24.4. Переходные и релаксационные процессы в несовершенных диэлектриках. Процессы в полупроводящих средах должны удовлетворять уравнению непрерывности: .
- •§24.7. Тензор магнитной проницаемости феррита. Сначала вспомним, что, на зывают прецессией.
- •§ 25.1. Вывод уравнений для Аи φ в переменном электромагнит-
- •§25.3. Комплексная форма записи запаздывающего векторного потенциала. В гл. 21 [см. Уравнение (21.27)] отмечалось, что состав- ляющая векторного потенциала от элемента линейного тока idl
- •§ 25.4. Излучение электромагнитной энергии.
- •§ 26.5. Аналогия между волноводом и линией с распределенными параметрами.
- •§ 27.7. Движение заряженных частиц в кольцевых ускорителях. Циклотрон представляет собой две полые камеры в виде полуцилиндров нз проводящего неферро-
- •§ 28.2. Уравнения магнитной гидродинамики. Систему уравнений магнитной гидродинамики образуют следующие группы уравнений.
- •§ 28.7. Эффект сжатия (пинч-эффект). В цилиндрическом столбе электрической дуги (рис. 28.4) нити тока параллельны'. Каждый элемент этой нити находится в маг-
- •§ 28.9. Принцип работы магнитного гидродинамического генератора. Через канал с большой скоростью V продувают плазму, нагретую до высокой температуры
- •Часть III
§ 21.7. Выражение проекций ротора в цилиндрической и сферической системах координат. Без вывода приведем выражение проекций
ротора H:
в сферической системе координат:
в цилиндрической системе координат:
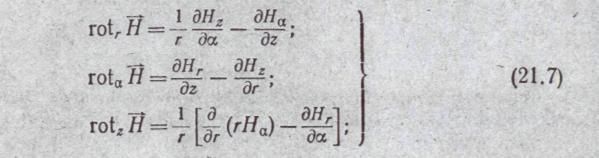 §
21.8. Принцип непрерывности магнитного
потока и запись его в
дифференциальной
форме.
Магнитный, поток есть поток вектора
магнитной
индукции через некоторую поверхность:
Ф = ∫ В dS.
§
21.8. Принцип непрерывности магнитного
потока и запись его в
дифференциальной
форме.
Магнитный, поток есть поток вектора
магнитной
индукции через некоторую поверхность:
Ф = ∫ В dS.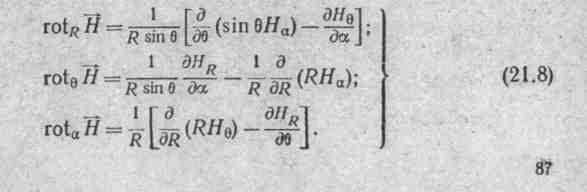
. S .
Индекс
S
под знаком.интеграла свидетельствует
о том, что интеграл
взят по поверхности S. Если поверхность
замкнута сама на себя (например,
поверхность шара), то поток, пронизывающий
замкнутую поверхность,
Ф =
 BdS.
BdS.
Опыт показывает, что вошедший внутрь любого объема магнитный поток равен магнитному потоку, вышедшему из того же объема.
Следовательно, алгебраическая сумма вошедшего в объем и вышедшего из объема потоков равна нулю:
 BdS.=
0. (21.9)
BdS.=
0. (21.9)
Выражение (21.9) представляет собой математическую запись прин- ципа непрерывности магнитного потока. Разделим обе части (21.9) на объем V, находящийся внутри замк- нутой поверхности S, и найдем предел отношения, когда объем V стремится к нулю:
![]()
Соотношение (21.10) можно трактовать как дифференциальную форму принципа непрерывности магнитного потока. Оно пригодно для любой точки магнитного поля. Следовательно, в любой точке этого поля нет ни истока, ни стока линий вектора магнитной индукции. Линии вектора Д нигде не прерываются, они представляют собой замкнутые сами на себя линии (окружность — пример замкнутой на себя линии).
Но линии H в точках, где изменяется j (например, на границах сред с разными µ.), прерывны. Это следует из (21.10); div В — divµ0 (H+j).= 0. Отсюда div H = —div J. Сопоставьте с прерывностью линий Е и непрерывностью линий D в электрическом поле (см. § 19.39). , -
§21.9. Магнитное
поле в областях «занятых» и «не занятых»
постоянным
током.
Вихревыми
принято
называть поля, ротор которых отличен
от нуля. Так как для магнитного поля
постоянного тока rot
H= ,
то во всех. точках пространства, где
,
то во всех. точках пространства, где 0,
поле вектора H является
вихревым. В областях пространства, где
0,
поле вектора H является
вихревым. В областях пространства, где
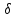 = 0,rot
H = 0, магнитное
поле можно рассматривать как потенциальное,
= 0,rot
H = 0, магнитное
поле можно рассматривать как потенциальное,
§
21.10. Скалярный
потенциал магнитного поля.
Для совокупности точек,
где
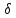 = 0,rot
H= 0,магнитное поле можно рассматривать
как
потенциальное, т. е. как поле, каждая
точка которого имеет скалярный
магнитный потенциал φм.
Следовательно, для таких областей можно
принять
= 0,rot
H= 0,магнитное поле можно рассматривать
как
потенциальное, т. е. как поле, каждая
точка которого имеет скалярный
магнитный потенциал φм.
Следовательно, для таких областей можно
принять
H=-gradφм
Так как div В = div µa H = 0, то при µa = const div H= 0. Подставив в последнее выражение —grad φм, вместо H, получимdiv grad φм, = 0.
Таким образом, скалярный потенциал магнитного поля φм, о котором может идти речь, только для областей, не занятых током, под- чиняется уравнению Лапласа:
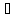 2φм=
0. (21.12)
'
2φм=
0. (21.12)
'
Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2
(см. стр. 352): UM12= φм1- φм2 = ∫2 H dl.
Падение магнитного напряжения между точками 1 и 2 по какому-то одному пути (например, по пути 132, рис. 21.5, а) равно падению маг- нитного напряжения между теми же точками по какому-то другому
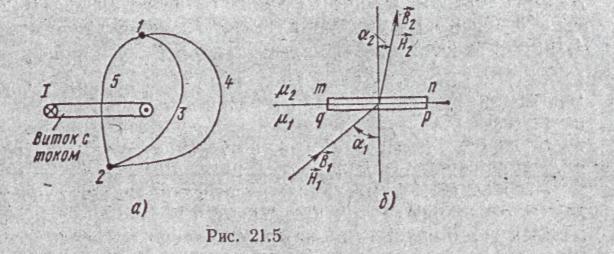
пути (например, по пути 142) в том случае, когда эти пути образуют замкнутый контур, ток внутри которого равен нулю.
Если
же замкнутый контур, образованный двумя
путями, охватывает; некоторый ток,
то падение магнитного напряжения по
первому пути
не равно падению магнитного напряжения
по второму пути — они
будут различаться на величину тока,
охваченного контуром. Последнее
вытекает из закона полного тока. Так,
применительно к рис. 21.5, a
∫ Hdl
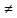 ∫
Hdl
(ибо из закона полного тока следует,
∫
Hdl
(ибо из закона полного тока следует,
152 132
что : ∫ Hdl +∫ Hdl=-I или ∫ Hdl = -I +∫ Hdl Следова-
132 251 132 152
тельно, для того чтобы разность магнитных потенциалов между двумя точками магнитного поля не зависела от пути, надо наложить запрет на прохождение через контур (виток) с током, мысленно натянув на этот . контур некоторую пленку. При прохождении через эту пленку φм изменяется скачком на величину тока в контуре.
Следует различать понятия «падение магнитного напряжения» и «магнитное напряжение». Первое определяется только линейным инте- гралом от H на dl по выбранному пути. Второе — не только этим
89
-
интегралом, но и м. д. с, имеющейся на пути (см. стр. 360). Здесь имеется полная аналогия с понятиями «падение напряжения» и «напряжение» в электрической цепи,
§ 21.11. Граничные условия. Подобно тому как в электростатическом поле ив поле проводящей среды выполнялись определенные граничные условия, в магнитном поле также имеют место аналогичные условия:
![]()
Условие (21.13) означает, что на границе раздела двух однородных и изотропных сред, различных в магнитном отношении (различные р.), равны тангенциальные составляющие векторов напряженности магнитного поля.
Условие (21.14) свидетельствует о равенстве нормальных составляющих векторов магнитных индукций на границе раздела.
Условие
(21.13) выводят путем составления линейного
интеграла
 Hdl
по
плоскому контуру mnpq
(рис.
21.5, б)
и
приравнивания его
нулю
(так как он не охватывает тока). Стороны
пр и
qm ничтожно
малы
по сравнению со сторонами тп
и
pq.
Длину
стороны тп
и
рав-
ную
ей по величине длину стороны pq
обозначим
через dl.
Тогда
Н1
sin
α1
dl
—
H2
sin
α2dl
=
0, но Н1
sin
α1
=
H1t,
Н2
sin
α2
= H2t,
следовательно
Н1t
=H2t
Hdl
по
плоскому контуру mnpq
(рис.
21.5, б)
и
приравнивания его
нулю
(так как он не охватывает тока). Стороны
пр и
qm ничтожно
малы
по сравнению со сторонами тп
и
pq.
Длину
стороны тп
и
рав-
ную
ей по величине длину стороны pq
обозначим
через dl.
Тогда
Н1
sin
α1
dl
—
H2
sin
α2dl
=
0, но Н1
sin
α1
=
H1t,
Н2
sin
α2
= H2t,
следовательно
Н1t
=H2t
Условие (21.13) не выполняется, если на поверхности раздела двух сред протекает так называемый поверхностный ток. Под ним понимают ток, протекающий по бесконечно тонкому плоскому проводнику, помещенному на границе раздела.
В этом случае
 Н
dl
будет
равняться не нулю, а поверхностному
току σdl,
который
оказался внутри замкнутого контура:
Н1
sin
α1dl
— H2
sin
α2
dl
= σdl
и в силу
этого H1t
— H2t
.= σ.
Другими
словами, при наличии поверхностного
тока с плотностью
а
тангенциальная
составляющая напряженности поля терпит
разрыв.
Как правило, поверхностный ток
отсутствует, и условие (21.13) выполняется.
Н
dl
будет
равняться не нулю, а поверхностному
току σdl,
который
оказался внутри замкнутого контура:
Н1
sin
α1dl
— H2
sin
α2
dl
= σdl
и в силу
этого H1t
— H2t
.= σ.
Другими
словами, при наличии поверхностного
тока с плотностью
а
тангенциальная
составляющая напряженности поля терпит
разрыв.
Как правило, поверхностный ток
отсутствует, и условие (21.13) выполняется.
Равенство
нормальных составляющих векторов
магнитной индукции
следует из принципа непрерывности
магнитного потока:
 В
dS
= 0.
В
dS
= 0.
Для
того чтобы убедиться в справедливости
(21.14), на границе раздела
выделим небольшой плоский параллелепипед
и подсчитаем потоки вектора B
через
нижнюю грань (рис. 21.6) —Bn1 S
и
верхнюю
B2n
S
и
верхнюю
B2n S.
S.
Сумма
потоков равна нулю: —Bln S
+ B2n
S
+ B2n S
= 0.
Следовательно,
В1п
= В2n.
S
= 0.
Следовательно,
В1п
= В2n.
Из (21.13) и (21.14) вытекает соотношение
![]()
90
Оно дает связь между углом падения α1 и.углом преломления α2 (см. рис. 21.5, б). Если магнитные силовые линии выходят из среды - большой магнитной проницаемостью, например μ1а = 104μ0, в среду малой магнитной проницаемостью, например в воздух μ2а = μ 0 то
![]()
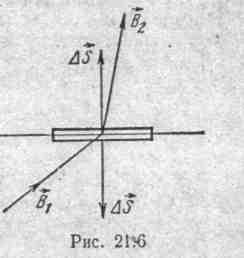
следовательно, угол α2 много мньше
угла α1
Пример 206. Найти угол α2, под которым лиловые линии выходят в среду с магнитной проницаемостью μ2а, если угол α1 = 89°;
μ 1a= 104μ0, μ 2a = μ0
Решение.
tgα1=
tg89°
= 57,29; tg
α2
= μ2/μ1 tgα1
=10
4
tg
α1
= 0,005729; α2
= 20'.
tgα1
=10
4
tg
α1
= 0,005729; α2
= 20'.
§ 21.12. Векторный потенциал магнитного поля. Для расчета магнитных полей широко используют векторный потенциал, или вектор-потенциал магнитного поля. Его обозначают А. Это векторная величина, плавно изменяющаяся от точки к точке, ротор которой равен магнитной индукции:
B= rotA (21.16)
Основанием для представления индукции в виде ротора от вектора- потенциала служит то, что дивергенция любого ротора тождественно равна нулю.
Известно, что в магнитном поле div B = 0. Подстановка в это равенство rot А вместо B дает выражение, тождественно равное нулю: div rot A= 0.
Равенство
нулю div
rot
А
можно
пояснить с помощью оператора
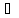 .
С этой целью.
вместо rot
А запишем
[
.
С этой целью.
вместо rot
А запишем
[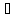 A].
Тогда div
rot
A
=
A].
Тогда div
rot
A
=
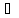 [
[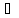 A].
Векторное
произведение [
A].
Векторное
произведение [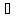 A]
перпендикулярно
и к
A]
перпендикулярно
и к
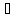 и к А.
Скалярное
произведение
и к А.
Скалярное
произведение
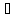 на[
на[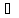 A],
т. е.
A],
т. е.
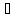 [
[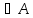 ],равно
нулю потому, что равен нулю косинус
угла между
],равно
нулю потому, что равен нулю косинус
угла между
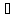 и[
и[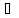 А].
А].
Если вектор-потенциал как функция координат известен, то индукцию в любой точке поля определяют путем нахождения ротора от вектора-потенциала в соответствии с (21.16). В отличие от скалярного магнитного потенциала φм, пользоваться которым можно только Для областей, не занятых током (см. § 21.10), векторным потенциалом можно пользоваться как для областей, не занятых током, так и для
областей, занятых ,током . В электротехнических расчетах векторный потенциал применяют для двух целей: 1) определения магнитной индукции с помощью формулы (21.16); 2) определения магнитного потока, пронизывающего какой-либо контур (см. § 21.14).
Векторный потенциал в произвольной точке поля связан с плотностью тока в этой же точке уравнением Пуассона.
Общее решение
их по аналогии с решением уравнения
(19.26) записывают так:
μа
rot
H=μa
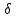
Условимся, что будем иметь дело с полями, которые можно под. разделить на отдельные области, так что магнитные проницаемости п., в каждой отдельной области постоянны. Если р., постоянна, то ее можно подвести под знак ротора:
rotμaH
= rotB
= μa
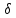 . (21.17)
. (21.17)
В (21.17) вместо В
подставим rot
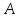 ,
тогда
,
тогда
rot
rotA
= μa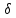 ; (21.18)
; (21.18)
Операция взятия
ротора от ротора есть по сути дела
операция
раскрытия двойного векторного
произведения и выполняется так:
rot
rot
A = [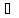 [
[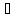 A
]] = grad
div
А -
A
]] = grad
div
А -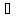 2A=
μa
2A=
μa
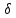 . (21.19)
. (21.19)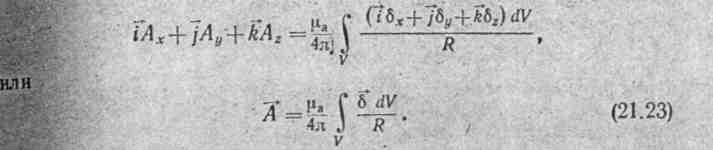
Из курса математики известно, что двойное векторное произведение раскрывается следующим образом: [а [b с]] = b (ас)—с(а b).
В
данном случае роль векторов а
и
b
играет
оператор
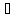 , а роль векторас—вектор-потенциал
А. Таким
образом, [
, а роль векторас—вектор-потенциал
А. Таким
образом, [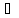 [
[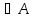 ]=
]=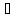 (
(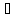 A)
—A
(
A)
—A
(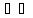 )
=grad
div
)
=grad
div
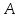 —
—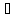 2A
2A
До сих пор к вектору-потенциалу никаких дополнительных требований не предъявлялось, если не считать того, что он должен быть функцией, имеющей пространственные производные. Так как A есть расчетная функция, то в магнитном поле постоянного тока ее можно подчинить требованию:
div A =0. (21.20)
Это требование означает, что линии вектора A есть замкнутые сами на себя линии. С учетом (21.20) уравнение (21.19) приобретает вид: -
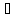 2A=
—
μa
2A=
—
μa
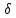 .
(21.21)
.
(21.21)
Уравнение
(21.21) представляет собой уравнение
Пуассона. В отличие
от (19.26), составленного относительно
скалярной величины φ, уравнение
(21.21)-составлено относительно векторной
величины. Вместо
A в (21.21) подставим
iAx
+jAy
+
kАz
и
плотность тока заменим
на i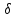 x
+j
x
+j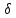 y
+k
y
+k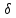 z
z
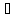 2
iAX
+
2
iAX
+
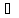 2jAy
+
2jAy
+
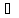 2
kАz
= - μа
i
2
kАz
= - μа
i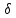 x
- μа
j
x
- μа
j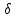 y-
μа
k
y-
μа
k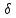 z
z
Последнее уравнение разбивается на три уравИения, составленные относительно скалярных величин Ах, Аy, Az '
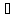 2Ax=
—
μа
2Ax=
—
μа
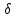 x
x
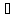 2Ay=
—
μа
2Ay=
—
μа
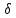 y
y
 2Az=
— μа
2Az=
— μа
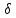 z
z
92
Если (21.22) умножить
на i, (21.22а) — на J
и (21.226)'— на
k и
. сложить, то получим
Единицей измерения
для A является В с/м.
с/м.
Формула (21.23) дает общее решение уравнения (21.21). Вектор- потенциал в любой точке поля может быть определен путем вычисления объемного интеграла (21.23). Последний должен быть взят, по всем областям, занятым током.
Несмотря на то что формула (21.23) дает общее решение, пользоваться ею в дальнейшем будем редко ввиду того, что взятие интеграла правой части формулы сопряжено обычно со значительными математическими выкладками. .
