§19.37, Поле точечного заряда, расположенного вблизи проводящей сферы.

Рассмотрим три родственные задачи на изображение в сфере.

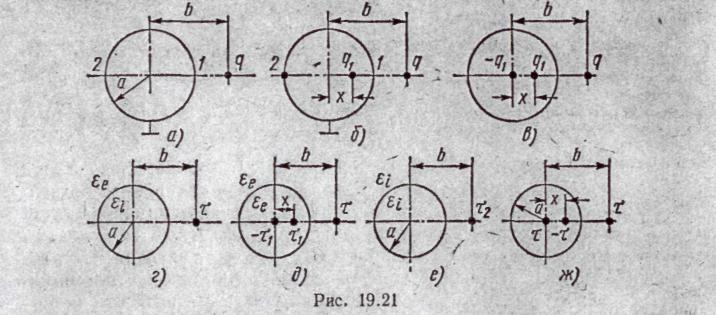
а. В диэлектрике с известной ε_а на расстоянии b от центра проводящего предварительно (до заземления) не заряженного шара радиуса а (см. рис. 19:21, а) поместим точечный заряд, q. Внутри шара поле известно (φ = 0 и Ε== 0).

Определим поле в пространстве вне шара. С этой целью на расстоянии x от центра шара поместим заряд q\ (рис. 19.21, б), составим выражения для потенциалов точек 1 и 2 шара приравняем их нулю (шар заземлен):

б. Если точечный заряд q поместить вблизи незаряженного незаземленного шара радиуса а, то поле вне шара определим как тюле от трех зарядов (рис. 19.21, в):

+С

.в. Если точечный заряд q поместить вблизи незаземленного шара с зарядом Q,то поле вне шара определится как поле от трех зарядов

Заряд q₁ помещен на расстоянии х от центра шара, a q₂ — в центре шара

§ 19.38. Поле заряженной оси, расположенной параллельно цилиндру. Рассмотрим две родственные задачи на изображение в диэлектрическом и проводящем цилиндрах.

а. В диэлектрике с электрической проницаемостью ε_е находится цилиндр, проницаемость которого ε_i;. Параллельно ему на расстоянии b от оси цилиндра расположена ось с зарядом τ на единицу длины (рис. 19.21,г). Поле вне цилиндра определяем по рис. 19.21, д. И цилиндр и окружающее его пространство заполнены средой сε_е,. Поле создается тремя зарядами: заданным τ, зеркальным зарядомτ₁ =

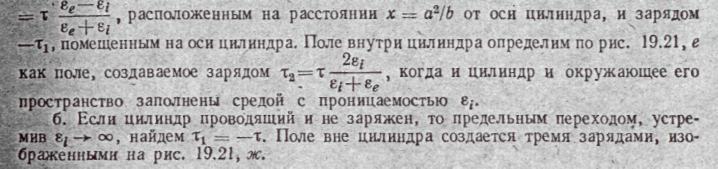
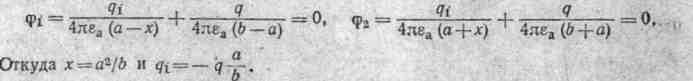
§19.39. Шар в равномерном поле. Если в равномерное поле (на­правлено сверху вниз: вдоль оси — z), напряженность которого

равна Е₀ (см. рис. 19.22), внести металличе­ский или диэлектрический шар (ε.шара отлично от ε окружающей среды), то электрическое поле, особенно вблизи шара, исказится, пере­станет быть равномерным. Характер искаже­ния поля зависит от размеров шара, его ε и от величины заряда на шаре.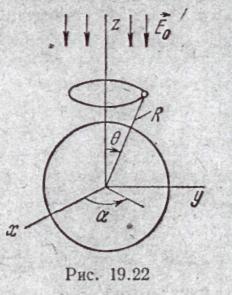

Если шар металлический (проводящий), то силовые линии должны подходить к его по­верхности под прямым углом. Если метали- ческий шар не заряжен, то на нем вследствие . явления электростатической индукции про­изойдет разделение зарядов. Силовые линии будут заканчиваться или начинаться на них.

Металлический шар может быть и заряжен, т. е. нести на себе избыточный заряд, который также расположится на поверхности.

Если шар из диэлектрика, то под влиянием внешнего по отношению к нему поля шар поляризуется. Заряды, выявившиеся на шаре вслед­ствие поляризации, исказят прежде (до внесения шара) равномерное 43

поле. Силовые линии будут подходить к поверхности шара так, что будут выполняться два граничных условия (см. § 19.23).

Если шар металлический, то внутри шара Е=0 и φ = const. Независимо от того, металлический шар или диэлектрический, во внешней по отношению к шару области нет. свободных зарядов и потому поле в наружной по отношению к шару области описывается уравне­нием Лапласа. Если шар из диэлектрика и свободный заряд на нем равен нулю, то поле внутри шара описывается также уравнением Лапласа.

Таким образом, для решения той и другой задачи необходимо проинтегрировать уравнение Лапласа 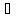²φ = 0. Это одна из наиболее типичных классических задач электростатики. Для любой конкрет­ной задачи необходим правильный выбор системы координат (пер­вый этап решения). Система координат должна быть выбрана таким образом, чтобы граничные поверхности в поле описывались наиболее удобно. В данной задаче граничная поверхность — сфера, которая наиболее удобно описывается в сферической системе координат. По­этому будем пользоваться этой системой.

Вторым этапом решения является выяснение вопроса о том, не обла-. дает ли изучаемое поле тем или иным видом симметрии. Условия симметрии поля часто в значительной мере облегчают решение задачи. В рассматриваемой задаче поле не зависит от координаты α. Чтобы убедиться в этом, мысленно рассечем поле плоскостью, перпендикулярной оси z декартовой системы, и проведем в этой плоскости окружность так, чтобы центр ее лежал на оси z. Все точки этой окружности имеют одно и то же значение радиуса R, соединяющего точку на этой окружности с началом координат. Кроме того, угол θ в меридианной плоскости между радиусом R и осью z один и тот же.

Все точки окружности находятся в поле в одинаковых условиях. Поэтому потенциал их один и тот же. Но значение угла а, характе­ризующего положения точек этой окружности, различно. Если для совокупности точек, обладающих R = const и θ = const и разными значениями угла α, φ одно и то же, то это означает, что в данном поле φ не зависит от угла.α. Поэтому поле будет описываться уравнением [см. уравнение (19.31)]:

(составляющая 1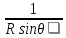* 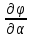выпала, так как φ не зависит от α). Выра-

жение (19.54) представляет собой уравнение в частных производных. Для интегрирования уравнений в частных производных применяют метод Фурьё, согласно которому, искомую функцию (в данном случае φ) полагают в виде произведения двух пока неизвестных функ­ций М и N, одна из которых (М) зависит только от R, а другая (N) — только от θ:

φ=M(R)N(θ) = MN (19.55)

' Вид функций М и N подлежит определению. Определение функ­ции φ в виде произведения двух функций (1.9.55) позволяет разбить

44 -

уравнение в частных производных (19.54) на два обыкновенных диф­ференциальных уравнения, из которых одно будет составлено отно­сительно М, другое — относительно N. Подставим (19.55) в (19.54), учтя, что

Поэтому

Умножим (19.66) на

Особенностью уравнения (19.57) является то, что первое слагаемое в нем представляет собой функцию только R, а второе слагаемое — функцию только θ. Сумма двух функций, из которых одна зависит только от R, а другая—только от θ, равна нулю для бесчисленного множества пар значений R и' θ [уравнение (19.57) годится для всех точек поля]. Это возможно тогда, когда каждая из данных функций равна нулю:

либо когда

Здесь р есть некоторое число, пока не известное.

Найдем интеграл второго уравнения:

Интеграл первого из них:

Таким образом, задача свелась к интегрированию уравнений (19.57') и (19.57"). Общее решение для φ согласно (19.55) равно произведению решений уравнений (19.57') плюс произведение решений для М и N по уравнениям (19.57"). Найдем решение уравнений (19.57'). Так как в (19.57') М зависит только от R, а N -—только от 9, то от част­ных производных можно перейти к простым (обыкновенным):

Покажем, что А₃ непременно должно равняться нулю, так как только в этом случае в решении отсутствует слагаемое А₃Intg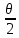

Потенциал есть функция непрерывная и на конечном отрезке он не может измениться на бесконечно большую величину. Из физических соображений ясно, что потенциал точек оси z вблизи шара не может быть равен бесконечности. Между тем, если быА₃ 0, то в решении

для потенциала присутствовало бы слагаемое А₃ Intg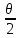, равное—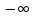

Полное решение: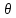

для всех точек, у которых= 0 (tgθ =0;Intgθ = —).

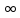при 8 = 0 t при 6=0

Таким образом, частное решение для φ, вытекающее из ('19;57'), следующее:

Найдем решение уравнений (19.57"):

или,

Применим подстановку Эйлера М ==CRⁿ:

Подставим производные в уравнение

Или n²+n-p=0

Определим корни квадратного уравнения:

Значение р определим при интегрировании второго уравнения (19.57: .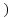

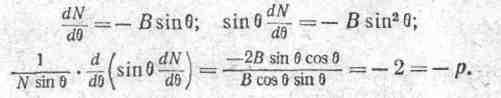
Следовательно, р = 2.

46

Решение его можно записать в виде N = В cosθ. Убедимся в этом путем подстановки и одновременно найдем значение р:

После нахождения числа р подставим его в (19.61) и найдем: п₁ = 1 ип_г = —2. Таким образом, совместное решение уравнений (19.57") дает следующее выражение для φ:

В (19.62) присутствуют четыре неизвестных постоянных: C_1, C₂, С₃ и С₄. Значения постоянных зависят от того, какой шар (проводя­щий или диэлектрический) внесен в поле *.