7.ОСНОВЫ ЯМР-СПЕКТРОСКОПИИ И ТОМОГРАФИИ

7.1История развития метода

Кнаиболее важным современным физическим методам исследования разнообразных объектов и сред относится ядерная магниторезонансная спектроскопия (ЯМР-спектроскопия), которая получила широкое

распространение и в медицине благодаря возможности получения изображений (ЯМР-томография). Эти методы основаны на анализе отклика среды на возмущение системы ядерных спинов электромагнитным полем. Явление ЯМР впервые экспериментально наблюдалось более 60 лет назад Блохом и Парселлом. Следующим важным этапом на пути развития метода стало открытие химического сдвига – величины, которая отражает изменение частоты сигналов ЯМР и характеризует электронное окружение рассматриваемого ядра. Информация о частоте сигналов дает представление не только об электронном окружении, но и о структуре химических соединений. В жидкостях первый спектр высокого разрешения был получен Арнольдом и относился к протонам гидроксильной группы, метиленовым и метильным протонам этанола. К этой области относится подавляющее большинство всех экспериментов по ЯМР в химии, фармакологии, биологии и медицине.

К общим недостатком ЯМР-методов относится их относительно низкая чувствительность, которая в значительной мере повышается путем применения фурье-спектроскопии (Р.Эрнст, 1966) и современных устройств со сверхпроводящими магнитами. Наибольшие успехи в применении метода ЯМР были достигнуты в исследованиях биологических макромолекул, что стало возможным в результате развития двумерной ЯМР-спектроскопии, предложенной Джинером и объективно заложившей основу ЯМР-томографии. Первые работы по применению ЯМР в биологии начались с исследования структуры протеинов малой массы в растворе, для которых ЯМР был использован как метод, альтернативный рентгеноструктурному анализу.

Идея и изложение основ нового метода медицинской визуализации объектов – ЯМР-томографии, были сформулированы в 1971 г. Лаутербурдом и Мэнсфилдом. В последние десять лет появилось много плодотворных приложений ЯМР в медицине, таких, как исследование биологических тканей in vivo, которые позволяют следить за ходом биологических процессов. Однако наиболее важным приложением ЯМР в медицине по-прежнему является томография биологических органов и организма в целом. ЯМР-томография основана на использовании магниторезонансных свойств биологических тканей и жидкостей человеческого организма и относится к методам неинвазивной диагностики. Сегодня развитие не только ЯМР-томографии, но и ЯМРспектроскопии, эффективно стимулируется именно ее широким применением в медицинской диагностике.

Медицинские диагностические ЯМР-изображения способны давать

информацию о пространственном распределении целого ряда физических характеристик биологических тканей, таких как спиновая плотность, постоянные времени спин-решеточной и спин-спиновой релаксации, величина химических сдвигов, скорость и направление движения биологических жидкостей. После соответствующей обработки ЯМР-изображения позволяют не только выявить те или иные патологии тканей и органов, но и определить их координаты, что очень важно для планирования и проведения хирургических операций. Потенциальные возможности ЯМР-томографии чрезвычайно велики: если удастся проводить исследование биомолекул в четко локализованных структурах (изолированные клетки и органеллы), то это откроет новые перспективы в клинической диагностике. Можно ожидать, что ценность ЯМРметодов для медицинских приложений будет возрастать.

Особое значение в биологии и медицине имеют спектры ЯМР на ядрах H1 , поскольку большинство биологических объектов состоит из соединений, в состав которых входит водород. Среди ядер, представляющих интерес и обладающих магнитным моментом, наряду с H1 можно назвать ядра P31 , C13 и N15 , однако естественное содержание изотопа C13 составляет лишь 1% к

изотопу C12 , а изотопа N15 – лишь 0,4%. Свойства ядер, представляющих интерес для биологии и медицины, приведены в таблице.

7.2 Условие резонанса

Движение отдельных частиц и молекул наиболее полно можно описать с помощью квантовой механики. Протоны и нейтроны, из которых состоят ядра атомов, обладают спином, поэтому многие ядра характеризуются отличным от

нуля полным механическим моментом количества движения Jˆ = Iˆ , где Iˆ - оператор ядерного спина. Благодаря этому атомные ядра обладают

определенным магнитным дипольным моментом µˆ , который связан с оператором механического момента простым линейным соотношением

µˆ =γJˆ = γIˆ , где γ - гиромагнитное отношение, которое является константой для

каждого типа ядер. Рассмотрение явления ЯМР с точки зрения квантовой механики для ядер водорода, а по существу – для протонов, является очень простым. Согласно закона Штерна и Герлаха частицы со спином I =1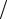2

располагаются в постоянном внешнем магнитном поле H0 не произвольным образом, а вдоль или против него, так что проекция спина на направление поля

Как и в любом виде спектроскопии, переходы между уровнями энергии могут быть индуцированы в том случае, если энергия электромагнитных

которое вытекает непосредственно из закона зеемановского расщепления спектра (7.1). В общем случае произвольного спина ядра возможные проекции спина на направление поля, например, на ось z , принимают значения

собственные значения энергии зеемановского расщепления спектров равны Em = − γmI H0 . Разность энергий соседних уровней есть γH0 , а резонансная

частота переходов между ними снова описывается выражением (7.2).

Если систему невзаимодействующих магнитных ядер, помещенных в постоянное магнитное поле, подвергнуть облучению высокочастотным РЧ полем с резонансной частотой (7.2), то это поле будет вызывать резонансные переходы между различными энергетическими состояниями магнитного момента ядер. В элементарном квантовомеханическом условии резонанса (7.2) отсутствует постоянная Планка, что указывает на возможность классической интерпретации явления ЯМР. Как известно, изменение момента количества движения определяется моментом действующих сил. Применительно к спину с

моментом J , находящемуся в постоянном магнитном поле H0 , это дает

ddtJ =[µ × H0 ]

поэтому классическое уравнение движения магнитного момента имеет вид

Здесь векторное произведение представляет собой вектор, направленный перпендикулярно к плоскости векторов µ и H0 , поэтому вектор µ описывает

конус вокруг H0 с постоянным углом θ при вершине.

Таким образом, вектор µ прецессирует против часовой стрелки (если смотреть по направлению вектора H0 ) с ларморовской частотой ω0 = γН0 , совпадающей с (7.2). Если теперь на ядерный спин кроме статического

магнитного поля H0 наложить еще и переменное магнитное поле H1 ,

перпендикулярное статическому полю, то в системе может наступить резонанс. Это происходит в случае, когда частота этого переменного поля равна частоте ω0 ларморовской прецессии магнитных моментов ядер. В результате в системе

наблюдается очень сильное взаимодействие, даже если переменное поле мало.

7.3Кинетика переходов

Вкубическом сантиметре воды содержится 1022 ядер атомов водорода, причем в отсутствие магнитного поля их магнитные моменты полностью

разупорядочены. При наличии поля число N+ спинов, проекция которых направлена вдоль приложенного поля, не совпадает с числом N− спинов,

ориентированных против поля. В состоянии термодинамического равновесия с окружающей средой отношение N− 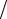N+ подчиняется соотношению Больцмана

N− = e−∆EkT ,

N+

где ∆E = γH0 . Уровень с меньшей энергией заселен больше и, следовательно,

большая часть спинов ориентирована по полю. При комнатной температуре в полях порядка 1Тл (10000Гс) относительная разность заселенностей всего лишь порядка 10-6. Это означает, что в 1см2 ориентированных по полю магнитных моментов ядер примерно на 1016 больше, чем ориентированных против. Однако эта небольшая величина позволяет провести измерение макроскопической намагниченности.

В состоянии термодинамического равновесия результирующая макроскопическая намагниченность направлена вдоль внешнего магнитного поля, а ее величина при комнатных температурах (так называемое высокотемпературное приближение) для системы ядерных спинов описывается выражением

где N0 = N+ + N− - полное число ядерных спинов в единице объема. Из этой

формулы видно, что макроскопическая намагниченность возрастает с увеличением напряженности магнитного поля и гиромагнитного отношения и убывает с ростом температуры. Такое поведение намагниченности определяет большое число эффектов, наблюдаемых в ЯМР.

Время T1 установления теплового равновесия между спиновой системой и

окружающей средой, которую принято называть решеткой (независимо от того, является ли вещество твердым телом, жидкостью или газом), определяется как время спин-решеточной релаксации. Эта величина описывает, например, процесс приближения z -компоненты намагниченности к равновесному значению M0 , которое устанавливается в системе спустя длительный

промежуток времени после приложения поля H0 :

Равновесная намагниченность устанавливается параллельно внешнему

Феноменолигическое уравнение, которому удовлетворяет разность заселенности уровней n = N+ − N− , имеет вид

∂n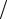∂t = −2w(n − n0 ) ,

где w- отнесенная к единице времени вероятность перехода между уровнями с повышением энергии состояния и n0 - максимальная разность заселенностей

уровней, соответствующая термодинамическому равновесию при данной температуре. Решение этого уравнения имеет вид

n(t) = n0 −{n0 − n(0)}e−2wt .

Подставляя это решение в (7.5) и сопоставляя получающееся выражение с (7.4), находим, что T1−1 = 2w . Существуют различные механизмы, которые могут

вносить вклад в вероятность перехода w. Эти механизмы, которые будут описаны ниже, в данном случае помогают установлению термодинамически равновесного значения намагниченности.

Под воздействием переменного поля резонансной частоты будут происходить вынужденные переходы с нижнего уровня на верхний, соответствующие поглощению энергии РЧ-поля, и обратные переходы, при каждом из которых выделяется квант энергии ω . Вероятности переходов w в единицу времени в обе стороны равны между собой, однако вследствие малого, но конечного избытка спинов на нижнем уровне число переходов снизу вверх в

единицу времени будет больше. Это приведет к поглощению энергии РЧ-поля и постепенному выравниванию заселенностей. Дифференциальное уравнение для изменения со временем величины n записывается теперь в виде

∂n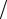∂t = −2wn ,

и имеет решение

n = n0 exp(−2wt) .

Таким образом, под воздействием переменного поля с течением времени разность заселенностей уровней стремится к нулю, что приводит к прекращению поглощения энергии высокочастотного поля (насыщение).