6. ПОГЛОЩЕНИЕ ЭМИ

6.1 Поглощение СВЧ волн в биологических тканях

По мере увеличения частоты (УВЧ-терапия, 20-100МГц) нет необходимости в использовании электродов, поскольку переменные токи смещения в тканях возникают непосредственно под действием электрического поля. Количество выделяемой теплоты

Q = 8ωπ ε′E 2 tgδ

уже не зависит от омического сопротивления биологической ткани и в соответствии с (6) определяется так называемым тангенсом угла диэлектрических потерь tgδ = ε′′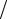ε′. Физиотерапевтические методы,

основанные на применении электромагнитных волн СВЧ-диапазона, делятся в медицине на ДЦВ-терапию (103 ÷104 МГц) и микроволновую терапию (частота более 10ГГц).

Большое значение для этих частотных диапазонов имеют токи смещения, обусловленные переориентацией дипольных моментов воды (характерная частота около 20ГГц). В связи с этим максимальное поглощение энергии микроволн происходит в таких тканях, как мышцы и кровь, а не в костной и жировой тканях, где воды существенно меньше. Таким образом, имеются большие различия в СВЧ-поглощении жировыми и нежировыми тканями, что связано с различным содержанием воды.

Если молекулы обладают постоянным дипольным моментом, то поглощение кванта энергии электромагнитного поля в диапазоне СВЧ излучения приводит к изменению вращательной энергии молекулы. Оператор дипольного момента в квантовой механике определяется как вектор

pˆ = ∑er ,

a

где суммирование производится по всем частицам. Средние значения оператора дипольного момента атома для его стационарных состояний равны нулю, однако это утверждение несправедливо в общем случае для молекул. Оператор

взаимодействия дипольного момента молекулы p с электрической

компонентой ЭМИ может быть записан в обычном виде V = −pE .

Для описания квантового поглощения энергии ЭМИ и соответствующего изменения энергии вращательного движения молекулы возможно применение общей теории переходов под влиянием возмущения, зависящего от времени. Возмущение в нашем случае является периодическим, а его матричные элементы переходов между стационарными состояниями Ψi и Ψf молекулы

можно представить в виде:

Vfi (t) = −12 pfi (t)E0 (t)e−iωt − 12 pif (t)E0 (t)eiωt =

= −12 pfi (t){E0 (t)e−iωt + E0 (t)eiωt },

pfi (t) = ∫Ψf pΨi drE0e =

= ∫(e−i E f tψ f ) p(e−i E f tψi )dr = pfi eiω fit ,

где ωfi = E f − Ei . Такой выбор оператора взаимодействия и его матричных

элементов в явном виде обеспечивает эрмитовость Vˆ(t). Подставляя второе из

этих выражений в первое и учитывая эрмитовость оператора дипольного момента, получаем

конечного состояния может быть как выше, так и ниже энергии начального. При ω > 0 для первого слагаемого в (6.1) основную роль будут играть состояния спектра энергии молекулы со значениями вращательной энергии Ef

в непосредственной близости к «резонансной» энергии Ei + ω , которая

больше энергии начального состояния. Для второго основную роль играют состояния с энергией Ei − ω , которая меньше начальной. Наоборот, при ω < 0

переходы с повышением энергии молекулы описываются вторым слагаемым, а с понижением – первым. Следовательно, в матричных элементах (6.1) достаточно рассматривать только первый член с близкой к нулю частотой ωfi −ω . Тогда вероятность перехода из первоначального стационарного

состояния в конечное за время t определяется этим матричным элементом и равна:

При больших временах стоящая в (6.2) функция пропорциональна t . Действительно, используя предельный переход

Спектр вращательных состояний по сравнению с колебательными и электронными можно считать практически непрерывным. По этой причине для того, чтобы различать конечные состояния непрерывного спектра в общем