Векторная алгебра и аналитическая геометрия

угла убывает от 1 до 0, таким образом, убывает от а до 0 в точке О(0, /2), и радиус-вектор точки М описывает верхнюю половину окружности. Нижняя её половина получается при изменении от 3 /2 до 2 . Этим значениям угла соответствуют положительные значения cos , возрастающие от 0 до 1, что приводит к возрастанию от 0 до а и геометрическому замыканию окружности.

Уравнение a cos задаёт окружность с центром в точке (a/2,0) и радиусом a/2.

2). В уравнении линии a cos перейдем к декартовым координатам:

каноническое уравнение окружности с центром в точке (a/2,0) и радиусом a/2. Постройте самостоятельно кривую asin , a > 0.

Спирали

Архимедова спираль: = а ,0 , 0 .

Для построения архимедовой спирали нужно вычислить значения при различных значения :

OA a ;OB 2OA 2 a ;OC 3OA 3 a ; и так далее.

2 2 2

Кривая представляет собой линию, описываемую точкой, движущейся с постоянной скоростью по лучу, вращающемуся около полюса О с постоянной

скоростью : a v .

Гиперболическая спираль: a , a > 0,0 , 0 .

40

Логарифмическая спираль:

строим кривую, содержащую косинус.

41

Четырехлепестковые розы:

Трёхлепестковые розы:

Лемниската Бернулли

Лемниската Бернулли - линия,

представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния.

В полярных координатах

2 2a2 cos2 .

Укажем, что точка М лежит на кривой, если выполнено условие

2

F1M F2M F1F2 .

2

Вершины кривой находятся в точках A(a2,0); C( a2,0). Площадь каждой петли S = a2.

42

Кардиоида

В полярных координатах a(1 cos ), a 0.

Вершина кардиоиды находится в точке А(2а,0).

Укажем, что площадь кардиоиды S 3 a2 , а длина

2

L = 8a.

3.6. Параметрическое задание линий

Параметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости.

Окружность

Пусть M(x,y) - текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью OX 0 t 2 . Из треугольника ОМА:

Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:

x2 y2 R2 (cos2 t sin2 t) R2 .

Циклоида

Циклоидой называется кривая, описываемая точкой круга, катящегося без скольжения по прямой линии.

Пусть Ox – прямая, по которой катится круг радиусом а. За параметр t примем угол поворота.

43

Параметрические уравнения циклоиды

y a(1 cost),

При 0 t 2 получаем первую арку циклоиды. Укажем, что длина дуги ОА1О1=8а, а площадь одной арки S = 3 a2.

Астроида

Астроидой называется кривая, которую описывает точка окружности радиуса R/4, когда окружность катится без скольжения внутри окружности радиуса R.

Параметрические уравнения астроиды

x Rcos3 t,

y Rsin3 t,

где 0 t 2 .

В декартовых координатах уравнение астроиды

x2/3+y2/3=R2/3.

Длина астроиды L = 6 R, а площадь, ограниченная астроидой, S = 3 R2/8.

44

4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Алгебраической поверхностью второго порядка называется поверх-

ность, уравнение которой в декартовой системе координат имеет вид:

Ax2+By2+Cz2+2Dxy+2Exz+2Fyz+Gx+Hy+Iz+K=0,

где не все коэффициенты при членах второго порядка равны одновременно нулю (в противном случае получаем алгебраическую поверхность первого порядка, т.е. плоскость).

В зависимости от значений коэффициентов возможны случаи, когда уравнение определяет вырожденную поверхность (пустое множество, точку, плоскость, пару плоскостей).

Например, уравнение x2 y2 z2 1 0 не имеет решений и задает пустое множество, уравнение x2 y2 z2 0 задает точку с координатами (0,0,0), задает плоскость х = 1, уравнение x2 y2 0 задает пару

плоскостей х = у и х = у.

Исследование формы поверхностей второго порядка по их каноническим уравнениям

Основным методом исследования формы поверхности по ее уравнению является метод сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями

x const; y const; z const.

Эллипсоид

Эллипсоидом называется поверхность второго порядка с каноническим уравнением

Рассмотрим сечение эллипсоида плоскостью z 0 . Линия пересечения эллипсоида и плоскости задается системой уравнений

Г – эллипс с полуосями а и b в плоскости z 0 .

Рассмотрим сечение эллипсоида плоскостью z h . Линия пересечения задается системой уравнений

45

Г – точка с координатами (0,0,c). Если h c , система решений не имеет, т.е. исследуемая поверхность не имеет общих точек с рассматриваемой плоскостью.

Далее, так как переменная z содержится в уравнении во второй степени, плоскость z 0 является плоскостью симметрии эллипсоида. Отсюда следует, что достаточно исследовать форму поверхности и построить ее часть в области z 0 , достроив затем остальную часть путем зеркального отражения найденного фрагмента поверхности относительно координатной плоскости ОXY.

Аналогично рассматриваются сечения поверхности плоскостями x const; y const.

Эллипсоид - замкнутая поверхность, имеющая три плоскости симметрии: x 0; y 0; z 0.

где –с < h < c, являются окружности, центры которых лежат на оси OZ и, следовательно, в этом случае эллипсоид является фигурой вращения с осью OZ.

Если a b c R , каноническое уравнение принимает вид x2 y2 z 2 R2

и задает сферу с центром в начале координат и радиусом R.

Гиперболоиды

Однополостный гиперболоид

Однополостным гиперболоидом называется поверхность второго порядка с каноническим уравнением

иопределяет эллипс с полуосями а и b.

Всечении плоскостью z h получаем эллипс

с большими, чем в предыдущем случае, полуосями

46

Сечение поверхности плоскостью x 0 дает уравнение линии пересечения в виде

дает гиперболу, пересекающую ось OZ.

Сечение плоскостью y 0 также задает гиперболу, пересекающую ось OZ. Двуполостный гиперболоид - поверхность, имеющая вид двух беско-

нечно расширяющихся чаш с тремя плоскостями симметрии: x 0; y 0; z 0.

Параболоиды

Эллиптический параболоид

Эллиптическим параболоидом называется поверхность с каноническим уравнением

47

Поверхность расположена в области z 0 . Сечениями в плоскостях z h являются эллипсы,

а в плоскостях x h č y h – параболы, в плоскости z 0 – точка (0,0,0).

Гиперболический параболоид

Гиперболическим параболоидом называется поверхность с каноническим уравнением

Применение метода сечений приводит к тому, что в плоскостях z h, где

h 0 (h 0) , обнаруживаются гипербо-

лы, а в плоскостях x h и y h 0 – параболы, в плоскости z 0 – пересекающиеся прямые.

Конус

Коническая поверхность – поверхность, с вершиной O и направляю-

щей G , содержащая все точки всех прямых (образующих), проходящих через точку O и пересекающихся с кривой G .

Каноническое уравнение конуса второго порядка имеет вид:

Метод сечений позволяет составить представление о форме этой поверхности.

Осью конуса, заданного рассматриваемым каноническим уравнением, является ось OZ. Сечения плос-

пересекающиеся прямые, проходящие через начало координат, сечения плоскостями x h и y h – гиперболы.

Сечения плоскостями, не параллельными координатным, распадаются на два класса. Если плоскость проходит через начало

координат, в сечении получаются пересекающиеся прямые (которые сливаются, если плоскость касается конуса). Если плоскость не проходит через начало ко-

48

ординат, то в сечении, по мере возрастания угла между нормалью к плоскости и осью конуса, возникают эллипсы (при малых углах), параболы (когда секущая плоскость параллельна какой-либо из образующих) или гиперболы (при больших углах).

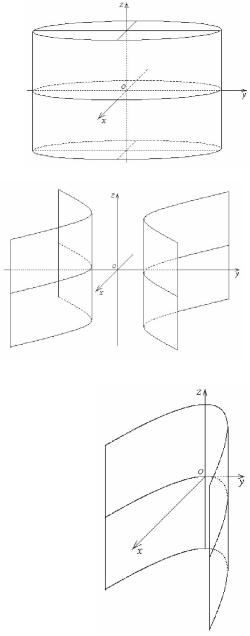
Цилиндры

Цилиндрическая поверхность — поверхность, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.

Эллиптический цилиндр

Эллиптический цилиндр задается канони-

ческим уравнением

Осью цилиндра является координатная ось OZ, поперечные сечения – эллипсы.

Гиперболический цилиндр

Гиперболический цилиндр задается каноническим уравнением

Параболический цилиндр

Параболический цилиндр задается каноническим уравнением

Если уравнение поверхности в канонической форме не изменяется при замене x x , y y , z z , то поверхность обладает центром симметрии и называется центральной. К ним относятся эллипсоид, однополостный и двуполостный гиперболоиды, конус, эллиптический и гиперболический цилиндры.

49