Решение

1) Определим напряжение на конденсаторе. Схема до коммутации приведена на рис. 2.2.6.а. Пользуясь символическим методом, определим комплексную амплитуду напряжения на емкости:

В.

Тогда его мгновенное значение определиться как:

В.

3) Послекоммутационная схема изображена на рис. 2.2.6.в. Напряжение на конденсаторе в установившемся режиме определим через его комплексную амплитуду:

В.

Тогда мгновенное значение этого напряжения:

В.

3) Запишем уравнение, составленное по второму закону Кирхгофа, для цепи, представленной на рис.2.2.6.а при замкнутом ключе К :

Учитывая, что ток в конденсаторе получаем следующее НДУ первого порядка:

ОДУ для напряжения имеет вид:

откуда находим характеристическое уравнение цепи и его корень:

с^-1.

Так как корень характеристического уравнения получается отрицательным и вещественным, то общее решение НДУ имеет вид:

Постоянную интегрирования находим из начальных условий:

где напряжение прикоторое в соответствии со вторым законом коммутации равно напряжению при

В.

Тогда

Итак, напряжение на конденсаторе изменяется по следующему закону:

В.

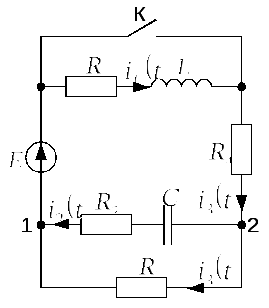
Задача 2.2.7 В цепи, изображенной на рис. 2.2.7.а в моментключ К замыкает накоротко катушку индуктивности. Данные цепи:В,Ом,Ом,мГн,мкФ. Рассчитать токиипосле замыкания ключа К.

рис. 2.2.7.а	рис. 2.2.7.б	рис. 2.2.7.в

Решение

1) Схема до коммутации приведена на рис. 2.2.7.б. Постоянный ток через конденсатор не течет, поэтому имеем:

А;

В.

Согласно законам коммутации получаем следующие независимые начальные условия:

А;

В.

2) Схема соответствующая установившемуся режиму работы цепи представлена на рис. 2.2.7.в.

Постоянный ток в заряженном конденсаторе

а катушка индуктивности зашунтирована ключом К поэтому данная цепь состоит лишь одного замкнутого контурав котором на основании второго закона Кирхгофа ток

А.

Тогда напряжение на емкости уравновешивается падением напряжения на резисторе от тока

В.

3) Для расчета переходного процесса для схемы, изображенной на рис. 2.2.7.а, в момент замыкания ключа К составим систему из пяти уравнений: первое и второе по первому закону Кирхгофа для узлов “1” и “2”, третье, четвертое и пятое – по второму закону Кирхгофа для контуровсоответственно:

где ток в конденсаторе.

Из третьего уравнения системы находим решение относительно тока в катушке

А.

Решим представленную систему относительно напряжения на конденсаторе для чего сделаем ряд подстановок:

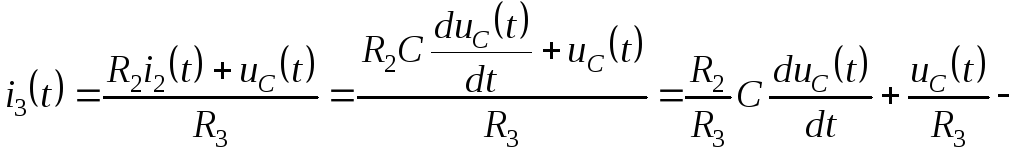
из пятого уравнения;

из четвертого;

из первого, которые введем во второе уравнение:

После группировки слагаемых имеем следующее НДУ первого порядка:

или в цифрах:

Приравняв правую часть НДУ к нулю, получим ОДУ

Тогда характеристическое уравнение

имеет один отрицательный корень

с^-1.

Общее решение составленного НДУ в случае одного отрицательного и вещественного корня имеет вид:

Из начальных условий определим постоянную интегрирования

откуда

В.

Итак, напряжение на емкости

В.

4) Рассчитаем искомые токи, пользуясь приведенными выше соотношениями:

Задача 2.2.8На рис. 2.2.8.а показана цепь, питаемая от источника переменного напряженияВ,рад/с. В моментключ К замыкает накоротко катушку индуктивности. Найти напряжение на конденсатореи ток в индуктивностии построить их графики для интервалов времени, охватывающих один период до и полтора периода после коммутации. Параметры цепи:Ом,мГн,мкФ. Решение 1) Рассчитаем реактивные сопротивления элементов:

Рис. 2.2.8.а