Вариант №15

1. Найти у

Х	-3	-2	-1	1	2	3
Р	0,1	0,2	0,2	у	0,2	0,1

2. M(X) =6, M(Y) = 2. Используя свойства математического ожидания, найдите M(2X - 3Y).

3. Вероятность появления события в одном опыте равна 0,4. Составить закон распределения случайной величины Х – числа появлений события в 4-х опытах. Найти ,и.

4. Два баскетболиста по очереди забрасывают мяч в корзину с вероятностью попадания для первого 0,9, для второго – 0,7. Составить таблицу распределения случайной величины Х – числа попаданий в корзину, если каждый баскетболист делает по одному броску. Найти ,,,.

5. В партии из 8 деталей – 6 стандартных. Наудачу отбирают 3 детали. Составить закон распределения дискретной случайной величины Х, числа стандартных деталей, среди отобранных. Найти математическое ожидание и дисперсию этой случайной величины.

6. Найти математическое ожидание и дисперсию, среднее квадратическое отклонение и функцию распределения дискретной случайной величины по следующей таблице:

Х	3	4	5	6	7
Р	0,1	0,3	0,2	0,3	0,1

Вариант №16

1. Найти у

Х	-4	-2	2	4
Р	0,1	0,2	0,3	у

2. M(X) =2.5. Используя свойства математического ожидания, найдите M(2X+5).

3. Составить закон распределения числа появления пятерки при трех подбрасываниях игрального кубика. Найти математическое ожидание и дисперсию числа появлений.

4. В партии из 9 деталей 5 стандартных. Наудачу отбираются для проверки 2 детали. Составить закон распределения дискретной случайной величины Х – числа бракованных деталей среди отобранных. Найти ,,.

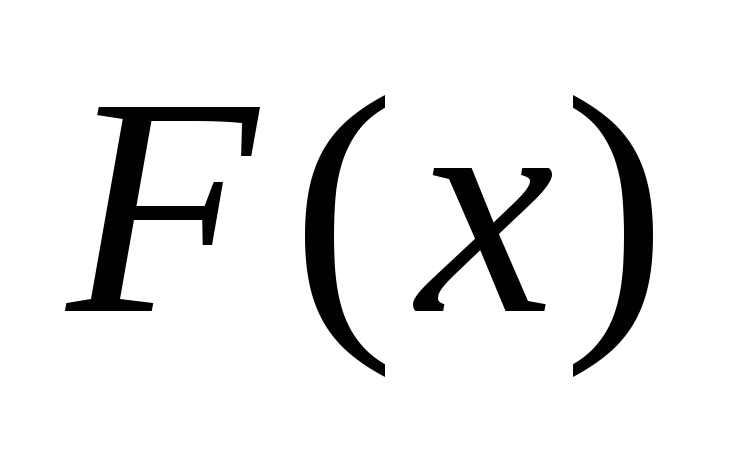5. В связке 5 ключей, из которых один подходит к двери. Дверь открывается путем опробований (предполагается, что опробованный ключ в дальнейших опробованиях не участвует). Составить таблицу распределения случайной величины Х – числа опробований. Найти и.

6. По таблице распределения Х:

Х	-3	-2	0	2	3
Р	0,2	0,1	0,2	0,3	0,2

Найти ,,. Найти.

Вариант №17

1. Найти у

Х	-2	-1	0	1	2
Р	0,1	0,2	0,4	0,2	у

2. D(X) =2.5. Используя свойства дисперсии, найдите D(2X+5).

3. Вероятность появления события в одном испытании равна 0,6. Производится 5 испытаний. Составить закон распределения случайной величины Х – числа появлений события. Найти ,,,.

4. В ящике 3 белых шара и 6 черных. Шары достают до тех пор, пока не появится белый шар. Составить закон распределения дискретной случайной величины Х – числа испытаний. Найти ,,и.

5. Рабочий обслуживает 4 станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого – 0,9, для второго – 0,8, для третьего – 0,75, для четвертого – 0,7. Найти математическое ожидание и дисперсию числа станков, которые не потребуют внимания рабочего в течение часа.

6. Найти ,, функцию распределения дискретной случайной величины, заданной таблицей:

Х	3	6	9	12	15
Р	0,3	0,1	0,3	0,2	0,1