Вариант №9
Найти у
|
Х |
-2 |
-1 |
0 |
1 |
2 |
|
Р |
0,1 |
0,2 |
0,4 |
у |
0,1 |
D(X) =4. Используя свойства дисперсии, найдите D(2X+5).
Монету подбрасывают 7 раз. Найти математическое ожидание и дисперсию числа появлений герба. Составить таблицу распределения Х – числа появлений герба.
В лотерее разыгрывается 400 билетов. В том числе 10 вещей по 5 р., 20 вещей по 10 р. и одна по 20 р. Составить закон распределения суммы выигрыша для владельца одного лотерейного билета. Найти
,
и
.В партии 7 деталей 3 бракованные. Контролер наудачу достает 4 детали. Составить закон распределения случайной величины Х – числа годных деталей в выборке. Найти математическое ожидание и дисперсию Х. Построить график функции распределения.
Найти математическое ожидание и дисперсию, среднее квадратическое отклонение и функцию распределения дискретной случайной величины по следующей таблице:
|
Х |
1 |
5 |
6 |
7 |
10 |
|
Р |
0,1 |
0,3 |
0,3 |
0,2 |
0,1 |
Вариант №10
Найти у
-
Х
1
2
3
5
Р
0,1
0,3
0,4
у
X и Y – независимы. D(X) =6, D(Y) =3. Используя свойства дисперсии, найдите D(2X+3Y).
Игральную кость бросили 12 раз. Найти математическое ожидание и дисперсию числа появлений единицы.
Игральный кубик брошен два раза. Составить закон распределения Х – числа выпавших очков. Найти
,
,
,
.Два стрелка делают по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,9, вторым – 0,8. Составить закон распределения случайной величины Х – числа попаданий в мишень. Найти
,
,
,
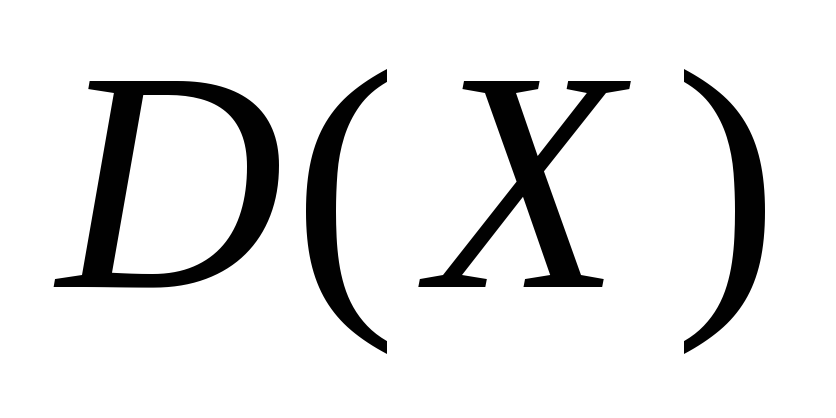.Случайная величина Х задана таблицей распределения
|
Х |
-2 |
1 |
2 |
3 |
|
Р |
0,3 |
0,2 |
0,4 |
0,1 |
Найти третий начальный и центральный момент и функцию распределения.
Вариант №11
Найти у
|
Х |
1 |
2 |
3 |
5 |
|
Р |
0,1 |
0,2 |
у |
0,6 |
M(X) =6, M(Y) =4. Используя свойства математического ожидания, найдите M(2X +3Y).
Изделия испытывают при перегрузочных режимах. Вероятности для каждого изделия пройти испытание равны 0,8 и независимы. Испытания заканчиваются после первого же изделия, после первого же изделия, не выдержавшего испытания. Найти распределение числа испытаний.
Два стрелка делают по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,9, вторым – 0,8. Составить закон распределения случайной величины Х – числа попаданий в мишень. Найти
,
,
,
.Два стрелка делают по одному выстрелу в мишень. Вероятность попадания первого равна 0,6, второго 0,8. Составить закон распределения числа попаданий Х. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение, третий центральный момент и функцию распределения. Построить график
.Найти математическое ожидание, дисперсию и функцию распределения случайной величины Х, заданной таблицей
|
Х |
1 |
2 |
3 |
4 |
|
Р |
0,3 |
0,5 |
0,1 |
0,1 |