
- •Федеральное агентство по образованию
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант №20
- •Вариант №21
- •Вариант №22
- •Вариант №23
- •Вариант №24
- •Вариант №25
- •Вариант №26
- •Вариант №27
- •Вариант №28
- •Вариант №29
- •Вариант №30
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Непрерывные и случайные величины
Индивидуальные задания
-
Пособие разработано доцентом Цыловой Е. Г., ассистентом Морозовой Е. А..
Одобрено методической комиссией кафедры «Высшая математика»
© 2007, каф. «Высшая математика» ПГТУ
Пермь 2007
Решение типового варианта
Задача 1. Модуль скорости молекулы
газа является случайной величинойX,
распределенной по закону Максвелла:![]() ,
если
,
если![]() ,
,![]() – параметр. Найти
– параметр. Найти![]() .
.
Решение: Плотность распределения
должна удовлетворять условию![]() ,
поэтому для нахождения значенияCпотребуем, чтобы выполнялось это условие:
,
поэтому для нахождения значенияCпотребуем, чтобы выполнялось это условие:![]() .
Воспользовавшись подстановкой:
.
Воспользовавшись подстановкой:![]() и значением гамма-функции получим:
и значением гамма-функции получим:![]() ,
и окончательно
,
и окончательно![]() .
Значение математического ожидания
получим, воспользовавшись формулой
.
Значение математического ожидания
получим, воспользовавшись формулой
![]() .
.
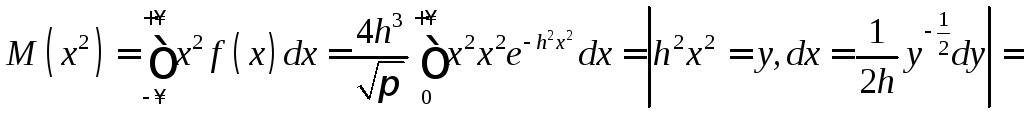
![]()
Дисперсия вычисляется по формуле:
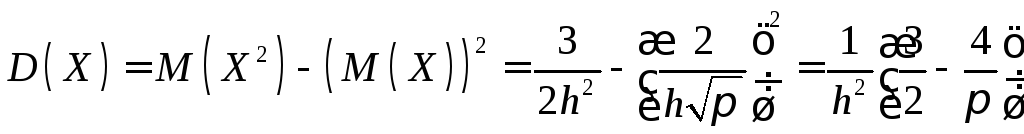 .
.
Задача 2. Задана плотность непрерывной случайной величины Х:
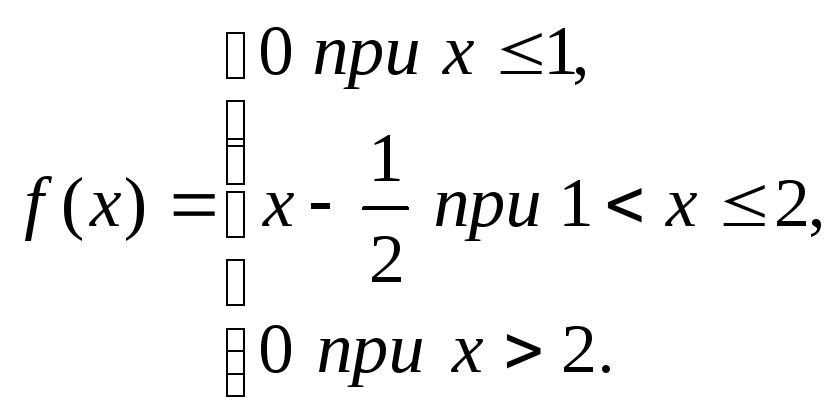
Найти функцию распределения
![]() .
.
Решение.Используем формулу![]() .
.
Если
![]() ,
то
,
то
![]() ,
следовательно
,
следовательно![]() .
.
Если
![]() ,
то
,
то![]()
Если
![]() ,
то
,
то![]() .
.
Итак, искомая функция распределения

При решении остальных заданий варианта необходимо использовать приведенные свойства с учетом свойств конкретных функций распределения.1
Вариант №1
Какой из этих графиков может соответствовать функции распределения непрерывной случайной величины, ответ обосновать
1)
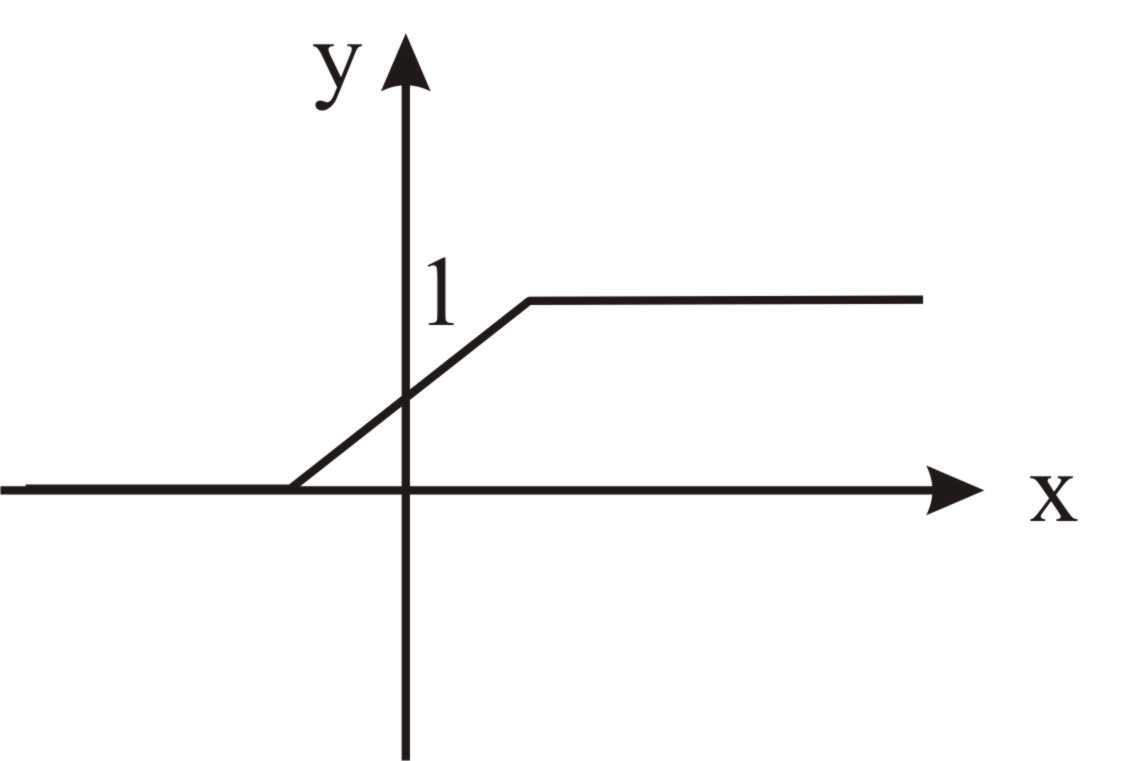
2)

3)

4)
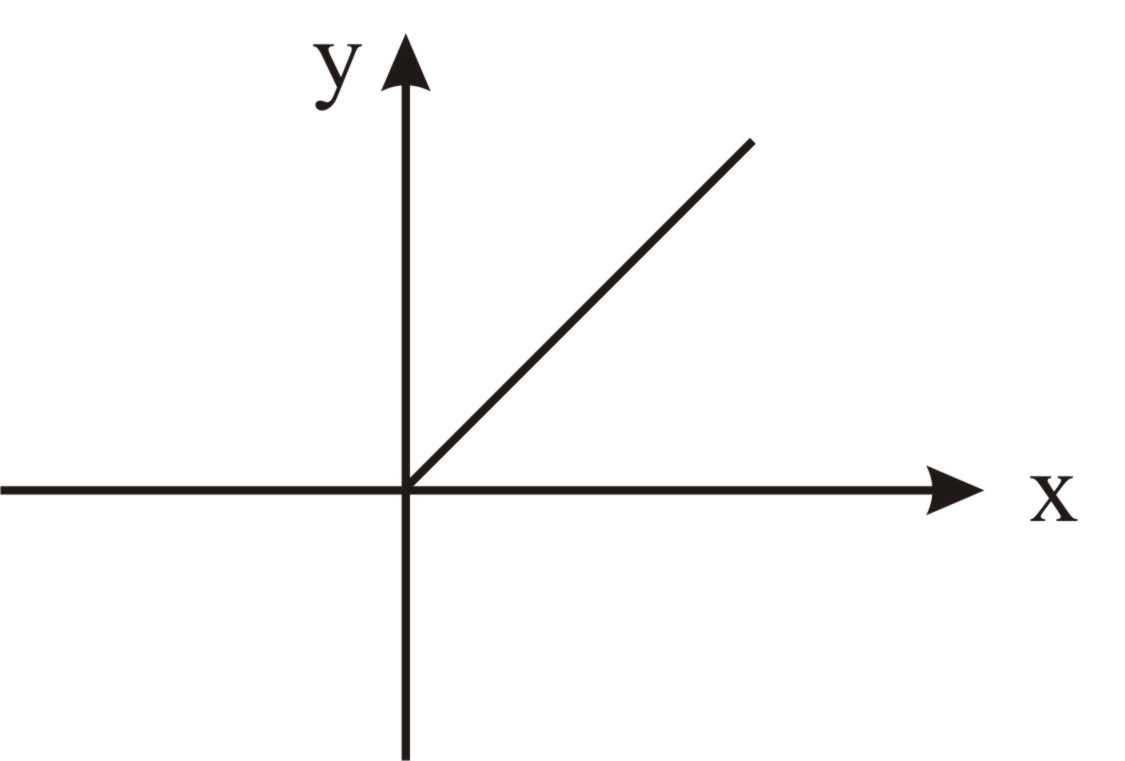
Задана функция распределения случайной величины Х. Требуется найти плотность распределения, математическое ожидание, среднее квадратическое отклонение. Построить графики функций плотности и функции распределения.
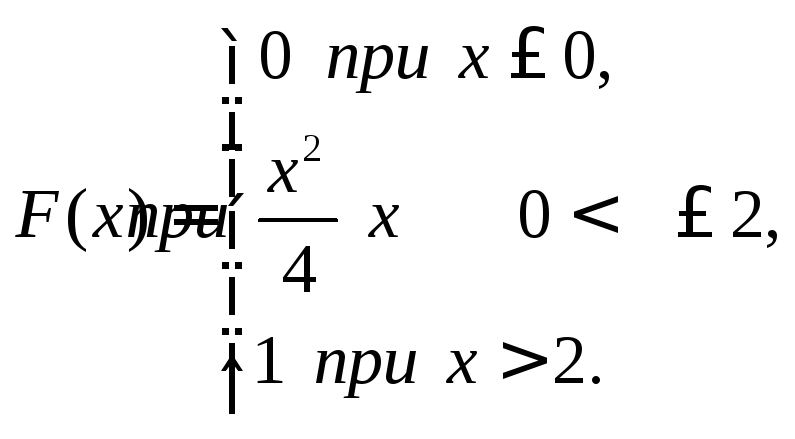
Случайная величина задана плотностью распределения
 .
Найти коэффициент С, математическое
ожидание и дисперсию. Найти
.
Найти коэффициент С, математическое
ожидание и дисперсию. Найти .
.
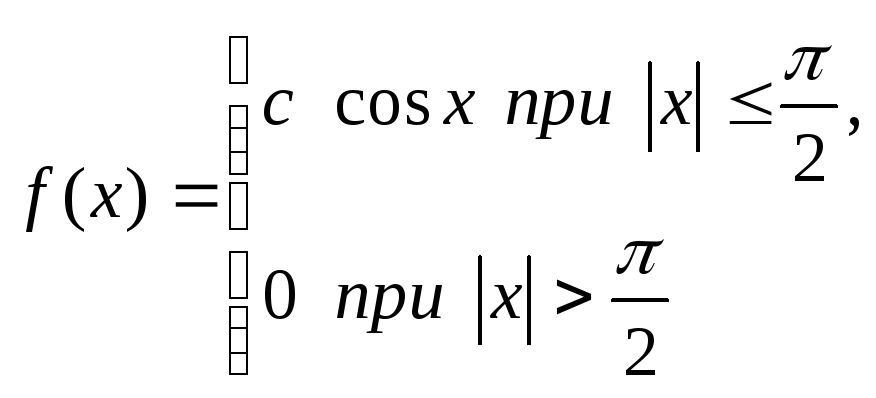
Случайная величина задана плотностью распределения
 .
Найти коэффициент С, математическое
ожидание и дисперсию. Найти
.
Найти коэффициент С, математическое
ожидание и дисперсию. Найти .
.
![]()
Случайная величина Xимеет равномерное распределение на отрезке от [0,6]. Написать выражение плотности. Найти
 ,
, и
и .
.Случайная величина Х имеет нормальное распределение с параметрами
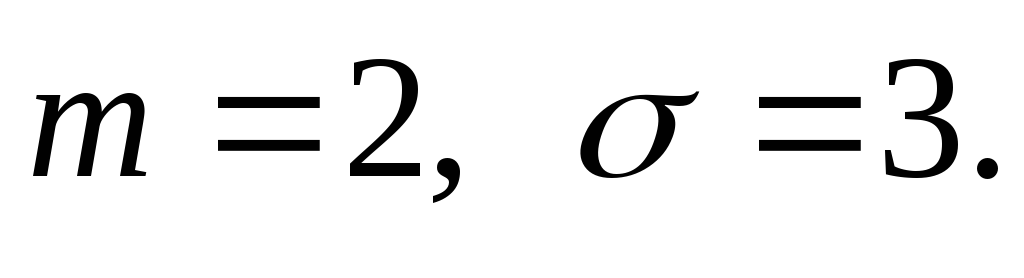 Написать
выражение плотности распределения,
нарисовать график плотности. Найти
вероятность того, что Х примет значение,
принадлежащее интервалу
Написать
выражение плотности распределения,
нарисовать график плотности. Найти
вероятность того, что Х примет значение,
принадлежащее интервалу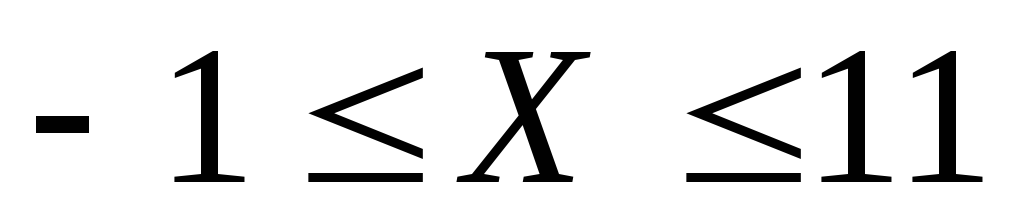 ,
а также вероятность неравенства
,
а также вероятность неравенства .
.
Вариант №2
Какой из этих графиков может соответствовать функции плотности распределения случайной величины, ответ обосновать
1)
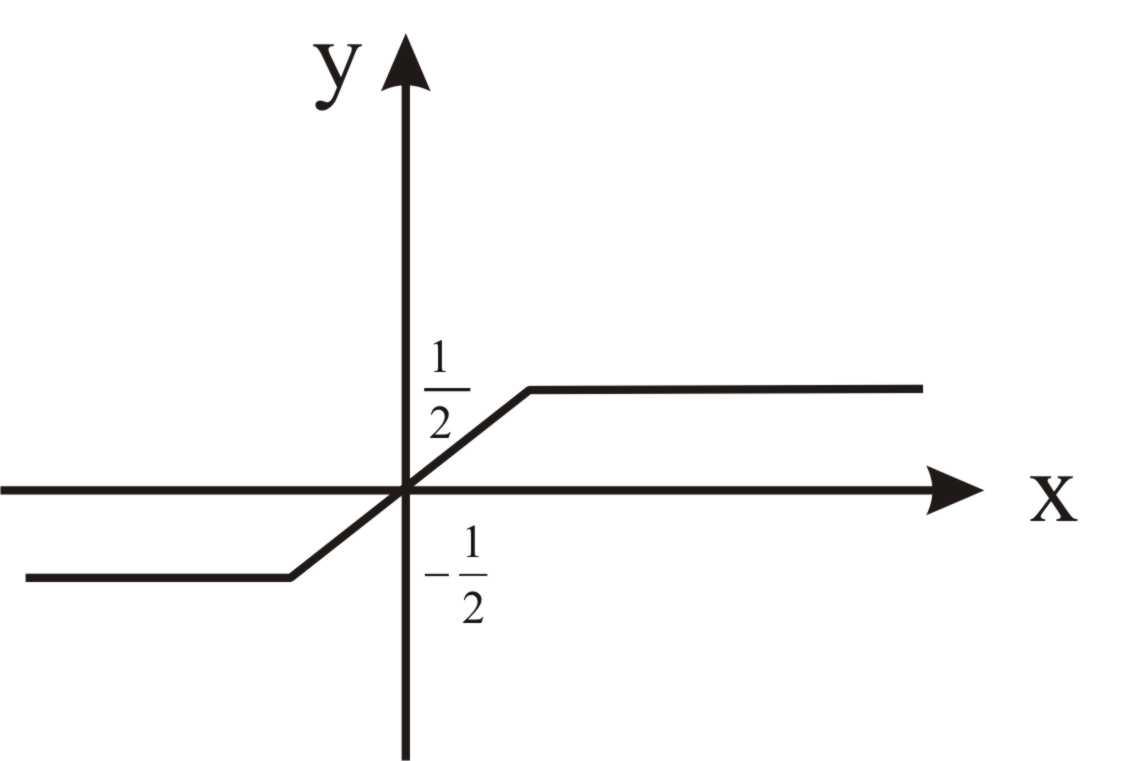
2)
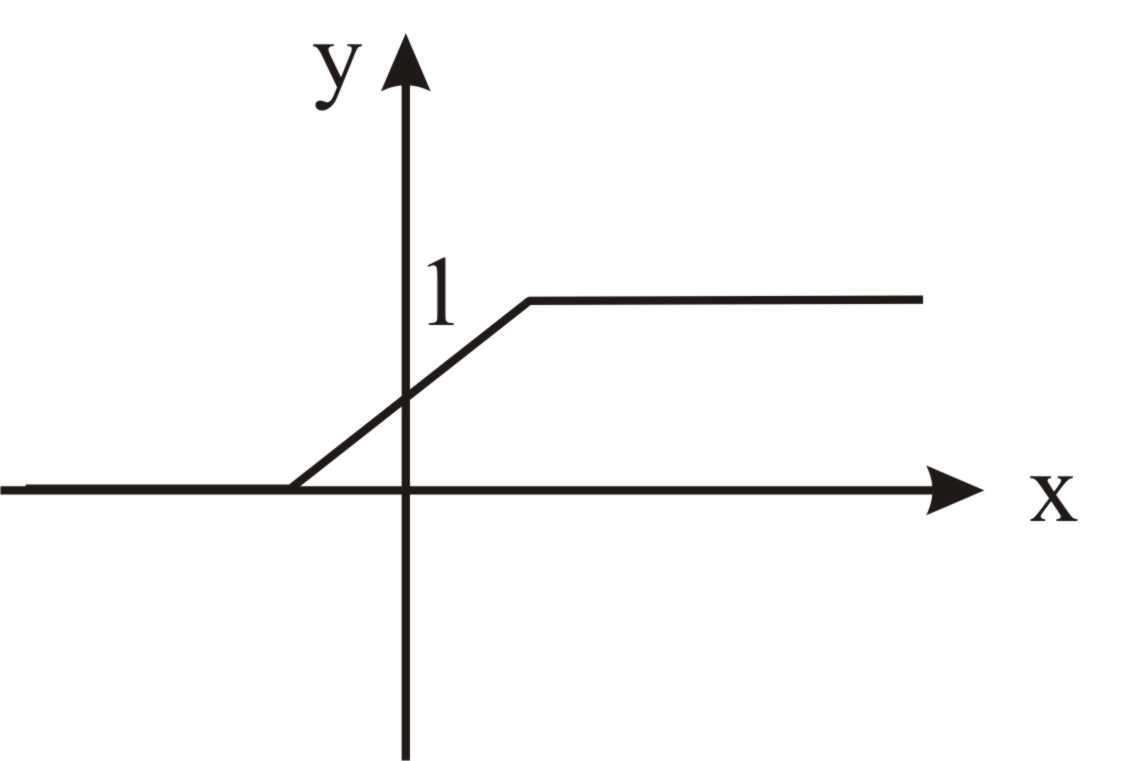
3)
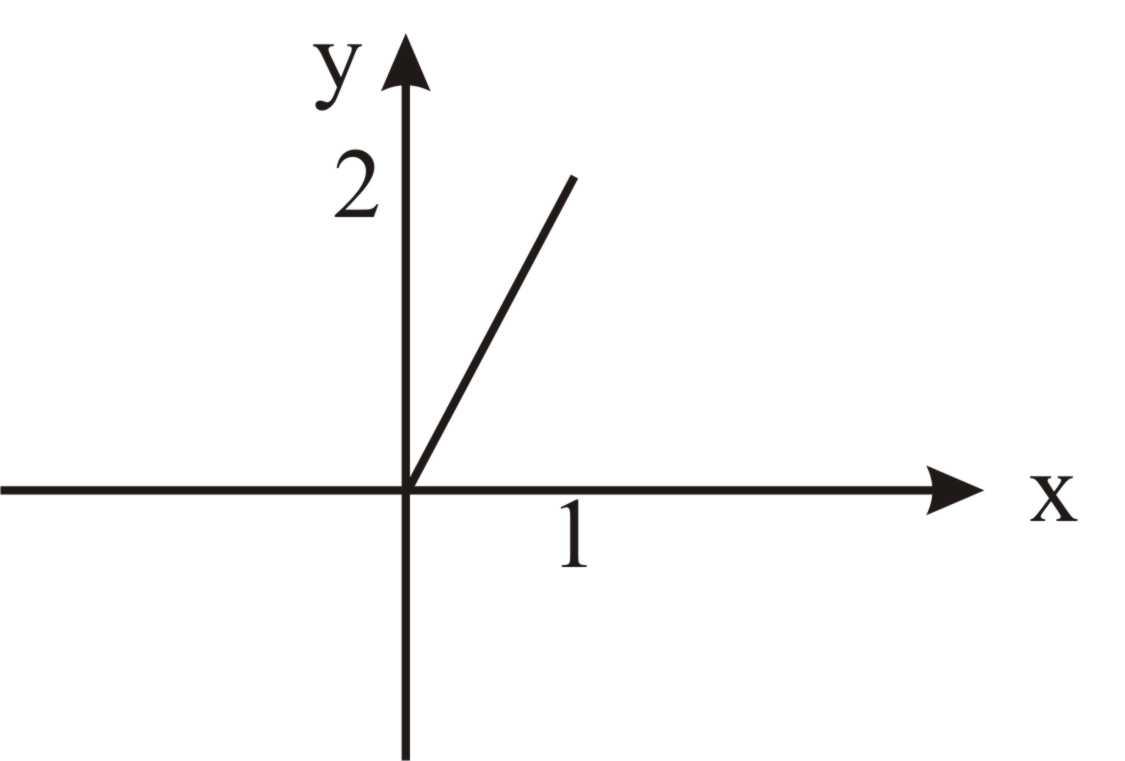
4)

Задана функция распределения случайной величины Х. Требуется найти плотность распределения, математическое ожидание, среднее квадратическое отклонение. Построить графики функций плотности и функции распределения.
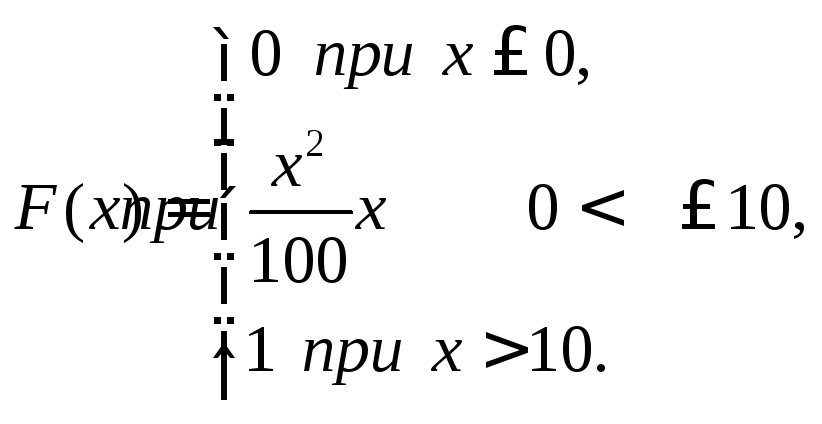
Случайная величина задана плотностью распределения
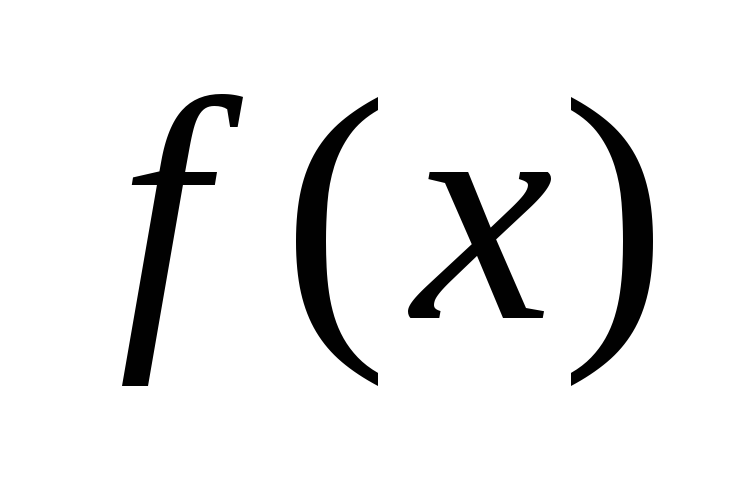 .
Найти коэффициент С, математическое
ожидание и дисперсию. Найти
.
Найти коэффициент С, математическое
ожидание и дисперсию. Найти .
.
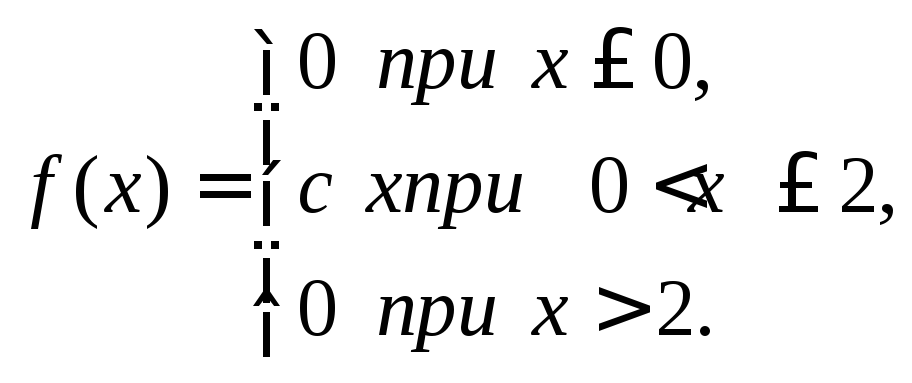
Случайная величина задана плотностью распределения
 .
Найти коэффициент С, математическое
ожидание и дисперсию. Найти
.
Найти коэффициент С, математическое
ожидание и дисперсию. Найти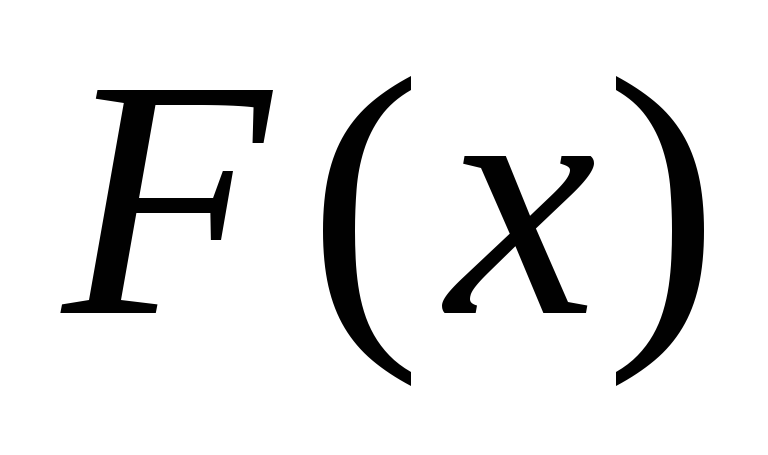 .
.
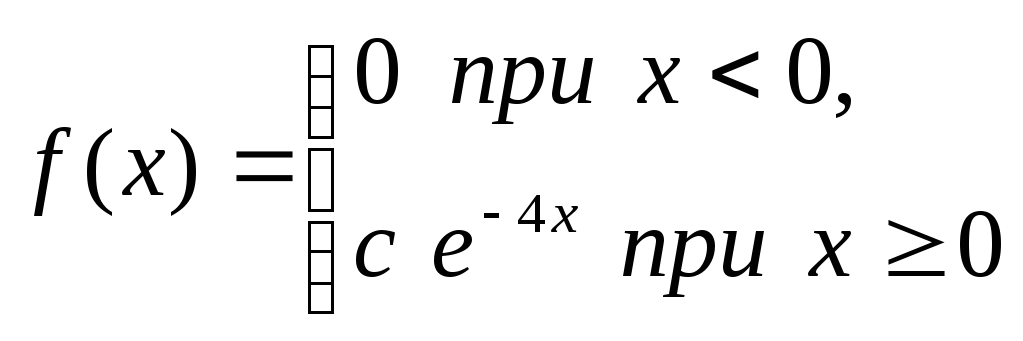
Случайная величина Xимеет равномерное распределение на отрезке от [2,6]. Написать выражение плотности и функции распределения. Найти
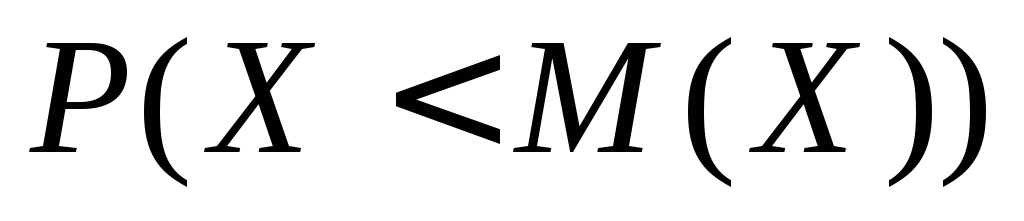 .
.Случайная величина Х имеет нормальное распределение с параметрами
 Написать
выражение плотности распределения,
нарисовать график плотности. Найти
вероятность того, что Х примет значение,
принадлежащее интервалу
Написать
выражение плотности распределения,
нарисовать график плотности. Найти
вероятность того, что Х примет значение,
принадлежащее интервалу ,
а также вероятность неравенства
,
а также вероятность неравенства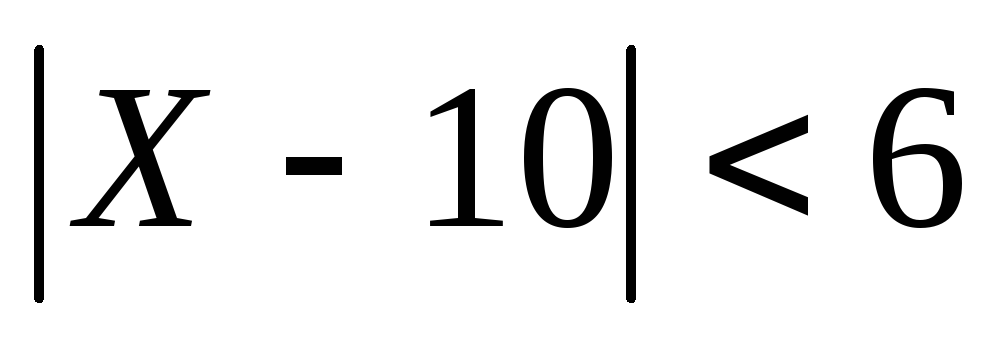 .
.
