
- •Федеральное агентство по образованию
- •Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
- •Вариант №11
- •Вариант №12
- •Вариант №13
- •Вариант №14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант №20
- •Вариант №21
- •Вариант №22
- •Вариант №23
- •Вариант №24
- •Вариант №25
- •Вариант №26
- •Вариант №27
- •Вариант №28
- •Вариант №29
- •Вариант №30
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Элементы теории функций комплексного переменного
Индивидуальные задания
-
Пособие разработано ассистентом Костиной Е.В., ассистентом Морозовой Е.А., доцентом Плаксиной В.П., ст. преп. Федосеевой О.А..
Одобрено методической комиссией кафедры «Высшая математика»
© 2007, каф. «Высшая математика» ПГТУ
Пермь 2007
Разбор типового варианта
Задание 1.
1) Найти модуль и аргумент чисел
![]() и
и![]() .
Изобразить числа на комплексной
плоскости. Представить числа в
тригонометрической и показательной
форме.
.
Изобразить числа на комплексной
плоскости. Представить числа в
тригонометрической и показательной
форме.
2) Найти: а).
![]() ;
б).
;
б).![]() ;
в).
;
в).![]()
Решение.
1) Изобразим числа на комплексной
плоскости. При этом числу
![]() будет соответствовать точка
будет соответствовать точка![]() ,
числу
,
числу![]() - точка
- точка![]() .
.

Для нахождения модуля и аргумента заданных чисел воспользуемся формулами:
![]() и
и
Получим:
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической и показательной применим формулы:
![]() и
и![]() .
.
Использовав ранее полученные результаты, получим:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2) а)
![]()
![]()
б)
![]()
![]()
в) Применим формулу
![]() .
.
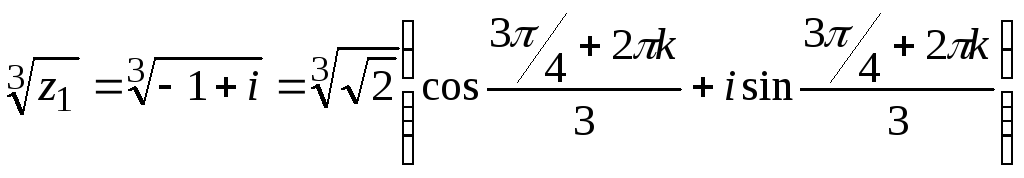
при
![]() :
: ;
;
при
![]() :
: ;
;
при
![]() :
:
![]()
Задание 2. Вычислить значение функции![]() в точке
в точке![]() ,
ответ представить в алгебраической
форме комплексного числа:
,
ответ представить в алгебраической
форме комплексного числа:
а)
![]() ;
;
б)
![]() .
.
Решение.
а)
![]()
б) По определению
![]() .
.
 ,
,

Задание 3. Указать область
дифференцируемости функции![]() и вычислить производную. Выделить
действительную и мнимую часть полученной
производной.
и вычислить производную. Выделить
действительную и мнимую часть полученной
производной.
Решение.
Выделим действительную и мнимую часть
функции
![]() :
:
![]()
Таким образом, получим:
![]()
Найдем частные производные
![]() и выясним, в окрестности каких точек
они существуют и непрерывны, а также в
каких точках плоскости выполняются
условия Коши-Римана:
и выясним, в окрестности каких точек
они существуют и непрерывны, а также в
каких точках плоскости выполняются
условия Коши-Римана:
![]() .
.
![]()
![]() ,
,
![]() ,
,
т.е.
![]() для любых действитедбных х и у, и эти
частные производные непрерывны во всей
плоскости
для любых действитедбных х и у, и эти
частные производные непрерывны во всей
плоскости![]() .
.
![]()
![]() ,
,
![]() ,
,
т.е.
![]() для любых действитедьных х и у, и эти
частные производные непрерывны во всей
плоскости
для любых действитедьных х и у, и эти
частные производные непрерывны во всей
плоскости![]() .
.
Так как условия Коши-Римана выполняются
для любой пары действительных чисел
![]() и частные производные
и частные производные![]() существуют и непрерывны в окрестности
любой точки
существуют и непрерывны в окрестности
любой точки![]() ,
то производная
,
то производная![]() существует в любой точке
существует в любой точке![]() комплексной плоскости С.
комплексной плоскости С.
Найдем эту производную:
![]()
![]()
![]()

Итак,
![]() .
.
Действительная часть производной:
![]()
![]() ,
,
мнимая часть производной:
![]() .
.
Задание 4.Определить вид кривой![]() .
.
Решение.
![]() .
.
Откуда
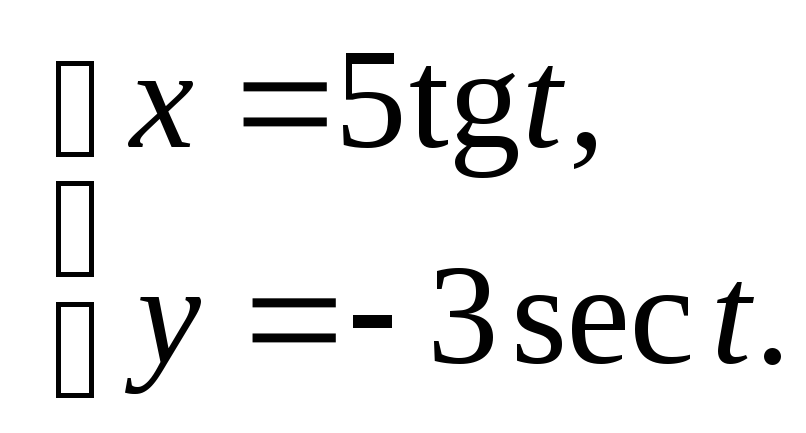
Выразим
![]() из каждого уравнения:
из каждого уравнения: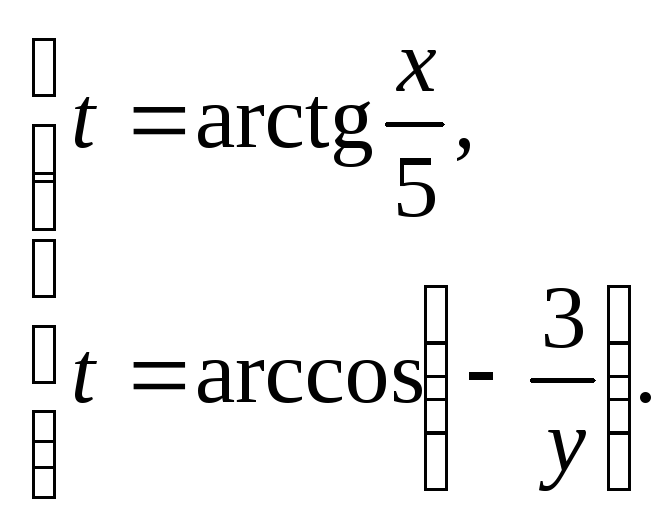
Исключим
![]() из уравнений:
из уравнений:
![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() - уравнение гиперболы.
- уравнение гиперболы.
Задание 5.Построить область плоскости![]() ,
определяемую данными неравенствами:
,
определяемую данными неравенствами:
а).

б).

а). Искомым множеством является пересечение
кольца
![]() и внутренней части угла
и внутренней части угла![]() :
:
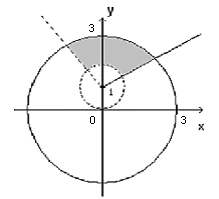
б). Кривую
![]() запишем в декартовых координатах:
запишем в декартовых координатах:
![]()
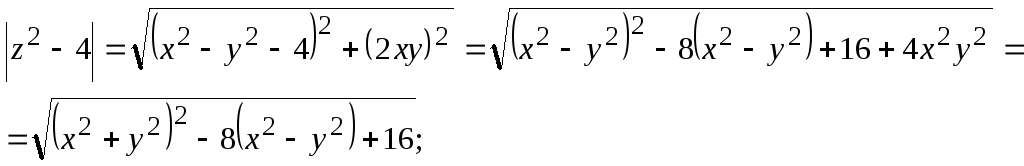
Итак,
![]() .
.
Или
![]() ,
,
![]() - Лемниската Бернулли.
- Лемниската Бернулли.
Неравенство
![]() определяет точки, лежащие на лемнискате
и внутри ее. Неравенство
определяет точки, лежащие на лемнискате
и внутри ее. Неравенство![]() определяет точки, лежащие правее прямой
определяет точки, лежащие правее прямой![]() Искомым
множеством является пересечение этих
областей:
Искомым
множеством является пересечение этих
областей:

Задание 6. Проверить, может ли функция![]() быть действительной частью некоторой
аналитической функции
быть действительной частью некоторой
аналитической функции![]() ,
если да – восстановить ее, при условии
,
если да – восстановить ее, при условии![]() .
.
Решение.
Найдем частные производные:
![]()
![]()
![]()
![]()
Следовательно,
![]() ,
,![]() .
.
Таким образом, функция
![]() гармоническая в плоскости
гармоническая в плоскости![]() ,
и, значит существует такая аналитическая
в
,
и, значит существует такая аналитическая
в![]() функция
функция![]() ,
что
,
что![]() .
.
В силу условий Коши-Римана имеем:
![]() (1)
(1)
![]() (2)
(2)
Интегрируем уравнение (1) по переменной
у, находим мнимую часть с точностью до
слагаемого
![]() :
:
![]() . (3)
. (3)
Продифференцируем (3) по х:
![]()
Сопоставляя результат с (2), получаем
![]() ,
откуда
,
откуда![]() .
.
Таким образом, имеем
![]() и
и![]()
Учитывая условие
![]() ,
получаем
,
получаем![]() .
.
Итак,
![]()
Задание 7.Найти область плоскости![]() ,
в которую отображается с помощью функции
,
в которую отображается с помощью функции![]() область
область![]() :
: плоскости
плоскости![]() .
.
Решение.
Для того чтобы найти образ области
![]() при отображении
при отображении![]() ,
нужно найти образ границы
,
нужно найти образ границы![]() области
области![]() ,
затем взять произвольную точку из
области
,
затем взять произвольную точку из
области![]() и найти ее образ.
и найти ее образ.
Правило для определения уравнения образа кривой.
Пусть в области
![]() кривая задана
кривая задана![]() .
Чтобы найти уравнение образа
.
Чтобы найти уравнение образа![]() этой кривой в плоскости
этой кривой в плоскости![]() при отображении с помощью функции
при отображении с помощью функции![]() ,
нужно исключить
,
нужно исключить![]() и
и![]() из уравнений:
из уравнений:
 (1)
(1)
Если кривая задана параметрическими уравнениями:
 или
или![]() ,
,
то параметрические уравнения её образа
при отображении
![]() будут
будут

В данном примере граница области
![]() состоит из трех частей:
состоит из трех частей:![]()
![]() .
Найдем ее образ при данном отображении.
.
Найдем ее образ при данном отображении.
Выделим и действительную и мнимую части функции.
![]() ;
;
![]() ,
,![]() .
.
Возьмем первую часть границы и найдем ее образ. Составим систему (1):

Возведем в квадрат первое и второе уравнения системы и сложим:
![]() .
.

Окончательное уравнение границы
![]() при
при![]() .
.
Аналогично находим образ
![]() :
:![]() при
при![]() .
.
Образ
![]() находим из системы:
находим из системы:

Следовательно, образ границы
![]() :
:![]() при
при![]() и
и![]() при
при![]() ;
;![]() .
Изобразим образы границ
.
Изобразим образы границ![]() на плоскости
на плоскости![]() .
.
Для изображения образа области
![]() на плоскости
на плоскости![]() возьмем контрольную точку. Точка
возьмем контрольную точку. Точка![]() обратится в точку
обратится в точку![]() .
.

Задание 8.Найти все лорановские
разложения данной функции![]() по степеням
по степеням![]() .
Указать главную и правильную части
ряда.
.
Указать главную и правильную части
ряда.
а)
![]() ,
,![]() ;
;
б)
![]() ,
,![]() .
.
Решение.
а) Функция
![]() имеет две особые точки
имеет две особые точки![]() и
и![]() .
Отметим их на плоскостиZ,
проведем 2 окружности с центром в точке
.
Отметим их на плоскостиZ,
проведем 2 окружности с центром в точке![]() ,
проходящие соответственно через точки
,
проходящие соответственно через точки![]() и
и![]() .
Следовательно, имеется три области, в
каждой из которых функция
.
Следовательно, имеется три области, в
каждой из которых функция![]() является аналитической:
является аналитической:
1 )
)![]() ;
;
2) кольцо
![]() ;
;
3) область
![]() ,
являющаяся внешностью круга
,
являющаяся внешностью круга![]() .
.
Найдем ряды Лорана для функции
![]() в каждой из этих областей, используя
формулу
в каждой из этих областей, используя
формулу
![]() (1)
(1)
справедливую при
![]() .
.
Представим функцию
![]() в виде суммы элементарных дробей:
в виде суммы элементарных дробей:
![]() .
.
1) Рассмотрим круг
![]() .
Запишем элементарные дроби
.
Запишем элементарные дроби![]() и
и![]() в виде
в виде![]() ,
где
,
где![]() при
при![]() .
Представим функцию
.
Представим функцию![]() следующим образом:
следующим образом: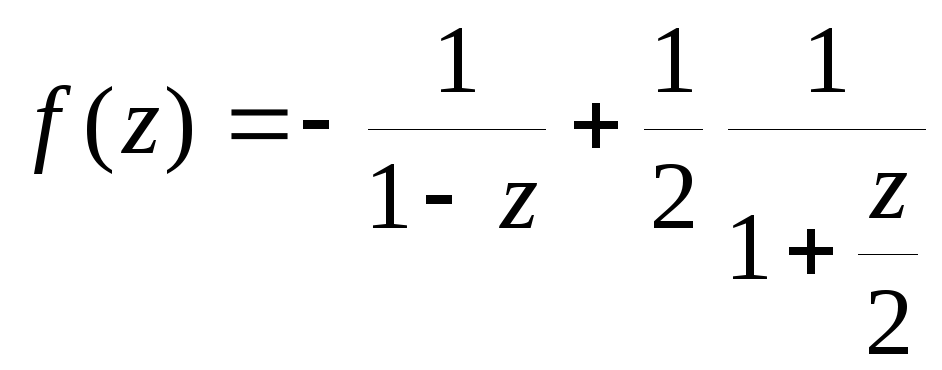 .
Теперь к таким дробям применима формула
(1).
.
Теперь к таким дробям применима формула
(1).
Так как в рассматриваемой области
![]() ,
то в силу формулы (1)
,
то в силу формулы (1)![]() .
Так как
.
Так как![]() и тем более
и тем более![]() (если
(если![]() ,
то тем более
,
то тем более![]() ),
значит, в силу формулы (1)
),
значит, в силу формулы (1)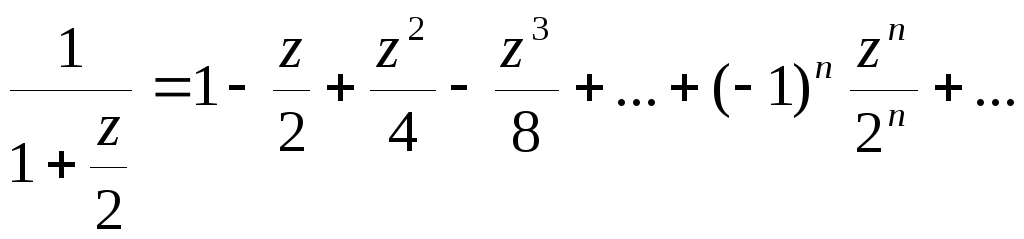 .
.
Следовательно,
 =
=![]() =
=![]()
![]()
Полученное разложение содержит только правильную часть ряда Лорана.
2) Рассмотрим кольцо
![]() .
В этой области запишем рассматриваемую
функцию в виде
.
В этой области запишем рассматриваемую
функцию в виде .
В знаменателях дробей мы записали
выражения вида
.
В знаменателях дробей мы записали
выражения вида![]() ,
где
,
где![]() .
.
Так как
![]() ,
то
,
то![]() и в силу формулы (1)
и в силу формулы (1) .
Так как
.
Так как![]() ,
то, как и в предыдущем случае,
,
то, как и в предыдущем случае, .
.
Следовательно,
 =
=![]() =
=![]() .
.
Полученное разложение содержит и правильную, и главную часть ряда Лорана.
3) Рассмотрим область
![]() .
В этой области
.
В этой области![]() ,
поэтому в силу формулы (1)
,
поэтому в силу формулы (1) .
.
В рассматриваемой области
![]() ,
значит
,
значит![]() и поэтому
и поэтому
 .
.
Функцию
![]() представим в виде
представим в виде .
В силу полученных разложений имеет
место равенство
.
В силу полученных разложений имеет
место равенство
![]() =
=![]()
![]() .
.
Полученное разложение содержит только главную часть ряда Лорана.
б) Функция
![]() имеет 2 особые точки
имеет 2 особые точки![]() и
и![]() ,
отметим их на плоскостиZ.
Точка
,
отметим их на плоскостиZ.
Точка![]() совпадает с точкой
совпадает с точкой![]() .
Проводим окружность с центром в точке
.
Проводим окружность с центром в точке![]() ,
проходящую через точку
,
проходящую через точку![]() .
.
Следовательно существуют две области,
в каждой из которых функция
![]() является аналитической:
является аналитической:
1 )
кольцо
)
кольцо![]()
2) кольцо
![]()
Найдем ряды Лорана для функции
![]() в каждой из этих областей, используя
формулу (1). Представим функцию
в каждой из этих областей, используя
формулу (1). Представим функцию![]() в виде суммы элементарных дробей:
в виде суммы элементарных дробей:
![]()
1) Требуется получить разложение функции
![]() по степенямz–1 в области
по степенямz–1 в области![]() .
Первая дробь уже представляет собой
степень
.
Первая дробь уже представляет собой
степень![]() .
Для того, чтобы вторую дробь представить
в искомом виде, сделаем замену
.
Для того, чтобы вторую дробь представить
в искомом виде, сделаем замену![]() ,
тогда
,
тогда![]() и
и![]() .
Дробь
.
Дробь![]() разложим по степеням
разложим по степеням![]() как в предыдущем примере. При
как в предыдущем примере. При![]() воспользуемся представлением:
воспользуемся представлением:
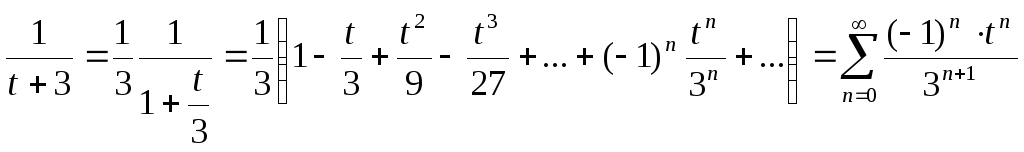 ;
;
Сделаем обратную замену. Получим, что
при
![]() функция
функция![]() представима в виде
представима в виде
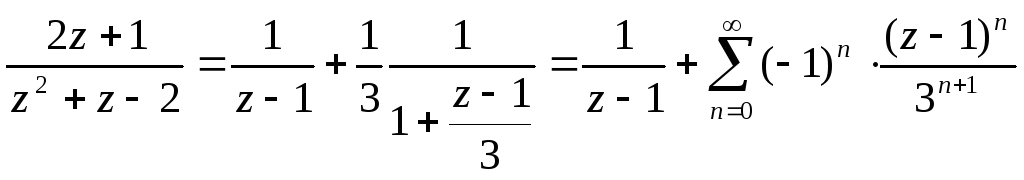 .
.
Полученное разложение содержит правильную и главную часть ряда Лорана.
2) Аналогично, сделав замену
![]() ,
получаем представление дроби
,
получаем представление дроби![]() в области
в области![]()
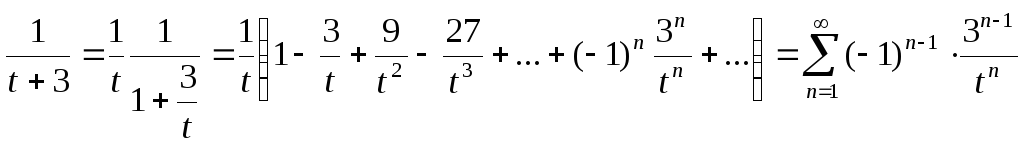
Сделав обратную замену, получаем, что
при
![]() функция
функция![]() представима в виде:
представима в виде:

![]() .
.
В первом случае главная часть ряда Лорана содержит только одно слагаемое, во втором случае ряд Лорана состоит только из одной главной части.
Задание 9.Разложить в ряд Лорана
функцию![]() в окрестности особой точки
в окрестности особой точки![]() .
.
Решение. Воспользуемся известным разложением:
 .
.
Задание 10.Для функции![]() найти изолированные особые точки,
провести их классификацию, вычислить
вычеты относительно найденных точек.
найти изолированные особые точки,
провести их классификацию, вычислить
вычеты относительно найденных точек.
a)![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Решение.
а). Особой точкой функции является точка
![]() .
Чтобы определить вид особой точки
разложим функцию в ряд Лорана по степеням
.
Чтобы определить вид особой точки
разложим функцию в ряд Лорана по степеням![]() :
:

Главная часть ряда Лорана содержит
конечное число слагаемых, значит
![]() - полюс. Порядок высшей отрицательной
степени
- полюс. Порядок высшей отрицательной
степени![]() определяет порядок полюса. Следовательно,
определяет порядок полюса. Следовательно,![]() - полюс кратности 2. Вычет найдем, используя
формулу
- полюс кратности 2. Вычет найдем, используя
формулу![]() ,
тогда
,
тогда![]() .
.
б). Особой точкой функции является точка
![]() .
Чтобы определить вид особой точки
используем признак поведения функции
в особой точке.
.
Чтобы определить вид особой точки
используем признак поведения функции
в особой точке.
![]() ,
значит
,
значит![]() устранимая точка и, следовательно
устранимая точка и, следовательно![]() .
.
в). Особой точкой функции является точка
![]() .
Чтобы определить вид особой точки
используем разложение функции в ряд
Лорана по степеням
.
Чтобы определить вид особой точки
используем разложение функции в ряд
Лорана по степеням![]() :
:
 Главная
часть ряда Лорана содержит бесконечное
число слагаемых, значит
Главная
часть ряда Лорана содержит бесконечное
число слагаемых, значит![]() - существенно особая точка. Тогда
- существенно особая точка. Тогда![]() ,
т.к. коэффициент при
,
т.к. коэффициент при![]() равен нулю.
равен нулю.
Задание 11. Вычислить интегралы от функции комплексного переменного:
а)
![]() ,
где
,
где![]() - отрезок прямой,
- отрезок прямой,![]() ,
,![]() .
.
б)
![]() ,
где
,
где![]() - ломаная,
- ломаная,![]() ,
,![]() ,
,![]() .
.
в)
![]() ,
где
,
где![]() - дуга окружности
- дуга окружности![]() ,
,![]() .
.
г)
![]() ,
где
,
где![]() - отрезок прямой
- отрезок прямой![]() ,
соединяющий точки
,
соединяющий точки![]() и
и![]() ,
,![]() и
и![]() .
.
Решение.
а) Так как подынтегральная функция
![]() аналитична всюду, то можно воспользоваться
формулой Ньютона-Лейбница:
аналитична всюду, то можно воспользоваться
формулой Ньютона-Лейбница:![]() =
=![]() .
.
б) Подынтегральная функция
![]() определена и непрерывна всюду, ломаная
определена и непрерывна всюду, ломаная![]() представляет собой кусочно-гладкую
кривую, поэтому искомый интеграл сводится
к вычислению двух криволинейных
интегралов по координатам по формуле:
представляет собой кусочно-гладкую
кривую, поэтому искомый интеграл сводится
к вычислению двух криволинейных
интегралов по координатам по формуле:
![]() .
.
Следовательно,
![]() .
.
Воспользуемся свойством аддитивности криволинейного интеграла:
![]() .
.
На отрезке
![]()
![]() ,
значит
,
значит![]() ,
,![]() .
Поэтому
.
Поэтому![]() .
.
На отрезке
![]()
![]() ,
,![]() ,
,![]() .
Поэтому
.
Поэтому
![]() .
.
Искомый интеграл
![]() равен
равен![]() .
.
в) Положим
![]() ,
тогда
,
тогда![]() ,
,![]() .
Следовательно,
.
Следовательно,
![]() =
=![]() .
.
г) Зададим линию
![]() параметрическими уравнениями:
параметрическими уравнениями:![]() ,
,![]() ,
,![]() ,
,![]() .
.
Для кривой, заданной параметрическими
уравнениями
![]() ,
,![]() ,
справедлива формула
,
справедлива формула .
.
Поэтому
![]() =
=![]() .
.
Задание 12.Вычислить интегралы, используя теорему Коши о вычетах:
а)
![]() ;
;
б)
![]() .
.
Решение.
а). Подынтегральная функция имеет внутри
контура интегрирования две особые точки
![]() и
и![]() .
Тогда
.
Тогда![]() .
.
Определим вид особых точек и найдем в них вычеты.
![]() ,
следовательно
,
следовательно![]() .
.
![]() ,
следовательно
,
следовательно![]() - полюс.
- полюс.
Так как
![]() ,
то
,
то![]() - полюс порядка
- полюс порядка![]() .
.
![]()
![]()
![]() .
.
Таким образом,
![]() .
.
б). Подынтегральная функция имеет внутри
контура интегрирования две особые точки
![]() и
и![]() .
Тогда
.
Тогда![]() .
.
Так как
![]() и
и![]() - полюсы первого порядка, то для вычисления
вычетов применим формулу
- полюсы первого порядка, то для вычисления
вычетов применим формулу![]() ,
где
,
где![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]()
Таким образом,
![]() .
.
Задание 13.Вычислить интегралы с помощью вычетов.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Решение.
а) Сформулируем правило, позволяющее вычислять несобственные интегралы от рациональной функции действительного переменного с помощью теории функций комплексного переменного:
Пусть
![]() - рациональная функция,
- рациональная функция,![]() ,
где
,
где![]() и
и![]() - многочлены степени
- многочлены степени![]() и
и![]() соответственно. Если функция
соответственно. Если функция![]() непрерывна на всей действительной оси
и
непрерывна на всей действительной оси
и![]() ,
т.е. степень знаменателя по крайней мере
на две единицы больше степени числителя,
то
,
т.е. степень знаменателя по крайней мере
на две единицы больше степени числителя,
то
![]()
где
![]() означает сумму вычетов функции
означает сумму вычетов функции![]() по всем полюсам, расположенным в верхней
полуплоскости.
по всем полюсам, расположенным в верхней
полуплоскости.
Так как подынтегральная функция
![]() четная, то
четная, то![]() =
=![]() .
Построим функцию
.
Построим функцию![]() ,
которая на действительной оси (при
,
которая на действительной оси (при![]() )
совпадает с подынтегральной функцией
)
совпадает с подынтегральной функцией![]() .
Особые точки функции
.
Особые точки функции![]() - это точки
- это точки![]() и
и![]() .
Из них в верхней полуплоскости находится
точка
.
Из них в верхней полуплоскости находится
точка![]() ,
которая является полюсом второго
порядка. Вычет функции
,
которая является полюсом второго
порядка. Вычет функции![]() относительно полюса
относительно полюса![]() равен
равен =
=![]() .
Так как в верхней полуплоскости только
одна особая точка, то
.
Так как в верхней полуплоскости только
одна особая точка, то![]() .
Следовательно,
.
Следовательно,![]() =
=![]() .
.
б) Сформулируем правило, позволяющее вычислить рассматриваемый несобственный интеграл с помощью теории функций комплексного переменного:
Пусть
![]() - рациональная функция,
- рациональная функция,![]() ,
где
,
где![]() и
и![]() - многочлены степени
- многочлены степени![]() и
и![]() соответственно. Если функция
соответственно. Если функция![]() непрерывна на всей действительной оси,
непрерывна на всей действительной оси,![]() ,
,![]() - произвольное действительное число,
то
- произвольное действительное число,
то
![]() ;
;
![]()
где
![]() означает сумму вычетов функции
означает сумму вычетов функции![]() по всем полюсам, расположенным в верхней
полуплоскости.
по всем полюсам, расположенным в верхней
полуплоскости.
Так как подынтегральная функция
![]() является четной, то
является четной, то![]() =
=![]() .
Построим функцию
.
Построим функцию![]() =
=![]() такую, что
такую, что![]() на действительной оси (при
на действительной оси (при![]() )
совпадает с
)
совпадает с![]() :
:![]() .
Отметим, что при
.
Отметим, что при![]() справедливо равенство
справедливо равенство![]() .
Функция
.
Функция![]() имеет в верхней полуплоскости полюс
первого порядка в точке
имеет в верхней полуплоскости полюс
первого порядка в точке![]() .
Вычет функции
.
Вычет функции![]() относительно этого полюса равен
относительно этого полюса равен![]() =
=![]() .
Следовательно,
.
Следовательно,![]() =
=![]() и
и![]() =
=![]() .
.
в) Сформулируем правило, позволяющее вычислить определенный интеграл функции, зависящей рационально от тригонометрических функций с помощью теории функций комплексного переменного:
Пусть
![]() - рациональная функция аргументов
- рациональная функция аргументов![]() и
и![]() ,
,![]() и функция
и функция![]() непрерывна внутри промежутка
интегрирования. Полагаем
непрерывна внутри промежутка
интегрирования. Полагаем![]() ,
тогда
,
тогда![]() ,
,![]() ,
,![]() ,
,![]() .
В этом случае
.
В этом случае
![]() =
=![]()
где
![]() есть сумма вычетов функции
есть сумма вычетов функции![]() относительно полюсов, заключенных
внутри окружности
относительно полюсов, заключенных
внутри окружности![]() .
.
В рассматриваемом интеграле применим
подстановку
![]() и после преобразований получим:
и после преобразований получим:![]() =
=![]() .
Внутри круга радиуса 1 с центром в начале
координат содержится только одна особая
точка подынтегральной функции
.
Внутри круга радиуса 1 с центром в начале
координат содержится только одна особая
точка подынтегральной функции![]() - это точка
- это точка![]() ,
которая является полюсом второго
порядка. Вычет функции
,
которая является полюсом второго
порядка. Вычет функции![]() относительно точки
относительно точки![]() равен
равен![]() =
=![]() .
Следовательно,
.
Следовательно,![]() =
=![]() .
.
