
Individualnye_zadania / 1_OprMatr
.docФедеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Матрицы и определители
Индивидуальные задания
-
Пособие разработано ст. преп. Зубко Т. Я., доцентом Седовой С. М., доцентом Сулавко Т. С..
Одобрено методической комиссией кафедры «Высшая математика»
© 2007, каф. «Высшая математика» ПГТУ
Пермь 2007
Задание к работе
1. Вычислить определитель 3-го порядка, используя метод Саррюса (или метод треугольников) и метод разложения по минорам какого-нибудь ряда.
2. Вычислить определитель высшего порядка.
3. Привести матрицу к ступенчатому виду и вычислить ранг матрицы.
4. Выполнить действия с матрицами.
5.
Вычислить значение многочлена от матрицы
![]() .
.
6.
Найти неизвестную матрицу
![]() из уравнения.
из уравнения.
Образец решения варианта.
1.Вычислить определитель 3-го порядка 1) по правилу Саррюса (правило треугольников). Это правило заключается в равенстве
 .
.
Таким образом,

2) Второе
правило вычисления
![]() называется разложением
называется разложением
![]() по элементам некоторой строки (или
столбца). Например, разложение по
элементам первой строки имеет вид
по элементам некоторой строки (или
столбца). Например, разложение по
элементам первой строки имеет вид
 .
.
Определитель

разложим по элементам третьего столбца, т.е.
![]()
![]() .
.
Как видно из приведенных примеров, вычисление определителей значительно упрощается, если какой-нибудь ряд определителя имеет только один элемент, отличный от нуля. Это можно всегда достигнуть, используя свойства определителей. В определителе

умножим первую строку на 2 и прибавим ко второй, прибавим первую строку к третьей, получим
 .
.
2. Вычислить определитель высшего порядка
 .
.
Решение :
Используя свойства определителя, понизим порядок определителя. С этой целью прибавим пятый столбец к первому :
 ;
;
в полученном определителе 4-го порядка четвертый столбец умножим на 3 и прибавим к первому столбцу, затем умножим его на 2 и прибавим ко второму столбцу, умножим его на 8 и прибавим к третьему столбцу, получаем
 .
.
Из приведенного примера очевидно, что вычисление определителей высших порядков значительно упрощается, если определитель привести к треугольному виду.
3. Привести матрицу к ступенчатому виду и вычислить ранг матрицы
 .
.
Решение.
Говорят,
что квадратная матрица имеет ступенчатый
вид, если ниже ее главной диагонали
стоят нулевые элементы. Матрица приводится
к ступенчатому виду с помощью элементарных
преобразований : а) перестановка строк,
б) умножение строки на число, в) прибавление
к одной строки другой, умноженной на
некоторое число. Ранг матрицы
![]() ,
,
![]() ,
равен количеству ненулевых строк
эквивалентной ей матрицы ступенчатого
вида.
,
равен количеству ненулевых строк
эквивалентной ей матрицы ступенчатого
вида.
В первом
столбце данной матрицы
![]() ниже первого элемента получим нулевые
элементы с помощью преобразования в).
Последовательно умножим первую строку
матрицы на (–2) и прибавим ко второй
строке, умножим на (–3) и прибавим к
третьей строке, умножим на (–2) и прибавим
к четвертой строке, получим
ниже первого элемента получим нулевые
элементы с помощью преобразования в).
Последовательно умножим первую строку
матрицы на (–2) и прибавим ко второй
строке, умножим на (–3) и прибавим к
третьей строке, умножим на (–2) и прибавим
к четвертой строке, получим
 .
.
В
полученной матрице во втором столбце
во второй строке и ниже второй строки
отсутствуют единицы. Единицу можно
получить, умножив вторую строку на (![]() ),
или поделив на (–5) , а затем во втором
столбце ниже второго элемента получить
нули с помощью преобразования в), при
этом будут возникать дробные числа. Во
избежание вычислений над дробями получим
единицу во втором столбце второй строки
иначе: ко второй строке прибавим третью
строку, умноженную на (–1), результат
запишем на месте второй строки. Далее,
поделим третью строку на (–2), четвертую
строку на (–1), имеем
),
или поделив на (–5) , а затем во втором
столбце ниже второго элемента получить
нули с помощью преобразования в), при
этом будут возникать дробные числа. Во
избежание вычислений над дробями получим
единицу во втором столбце второй строки
иначе: ко второй строке прибавим третью
строку, умноженную на (–1), результат
запишем на месте второй строки. Далее,
поделим третью строку на (–2), четвертую
строку на (–1), имеем
 .
.
Во втором столбце полученной матрицы ниже второго элемента получим нулевые элементы. Последовательно умножим вторую строку полученной матрицы на 2 и прибавим к третьей строке, умножим на 7 и прибавим к четвертой строке, затем третью строку поделим на 9 , четвертую строку поделим на 18. Во вновь полученной матрице в третьем столбце ниже третьего элемента получим нулевой элемент: третью строку умножим на (–1) и прибавим к четвертой строке, имеем
 .
.
Отсюда заключаем, что
![]() .
.
4. Выполнить действия с матрицами
 .
.
Решение. Обозначим
 ,
,
 ,
,
 ,
,
![]() .
.
Произведение
![]() имеет смысл, так как число столбцов
матрицы
имеет смысл, так как число столбцов
матрицы
![]() равно числу строк матрицы
равно числу строк матрицы
![]() .
Находим матрицу
.
Находим матрицу
![]() , элементы которой
, элементы которой
![]() ,
,
![]() . Имеем
. Имеем

 .
.
Произведение
![]() имеет смысл, так как тоже число столбцов
матрицы
имеет смысл, так как тоже число столбцов
матрицы
![]() равно числу строк матрицы
равно числу строк матрицы
![]() . Находим матрицу
. Находим матрицу
![]() , элементы которой
, элементы которой
![]() ,
,
![]() . Имеем
. Имеем

 .
.
Разность
![]() имеет смысл, так как матрицы
имеет смысл, так как матрицы
![]() и
и
![]() имеют одинаковую размерность
имеют одинаковую размерность
![]() . Находим искомую матрицу
. Находим искомую матрицу
![]() , элементы которой
, элементы которой
![]() ,
,
![]() . Имеем
. Имеем
![]()
 .
.
Ответ : Результатом действия данных матриц является матрица
 .
.
5.
Вычислить значение многочлена
![]() от матрицы
от матрицы
![]() ,
где
,
где
![]() ,
,
![]() .
.
Решение.
При
вычислении значения многочлена
![]() от матрицы
от матрицы
![]() вместо
вместо
![]() подставляем данную матрицу
подставляем данную матрицу
![]() ,
а свободный член многочлена записываем
в матричной форме, т.е. в виде
,
а свободный член многочлена записываем
в матричной форме, т.е. в виде
![]() ,
где
,
где
![]() единичная матрица того же порядка, что
и данная матрица
единичная матрица того же порядка, что
и данная матрица
![]() . Таким образом,
. Таким образом,
![]() ,
,
1)
![]()
![]() ,
,
2)
![]() ,
,
3)
![]() .
.
Имеем
![]()
![]() .
.
Ответ
:
![]() .
.
6.
1) Найти неизвестную матрицу
![]() из уравнения
из уравнения
![]() .
.
Решение.
Исходное уравнение запишем в матричной форме
![]() ,
где
,
где
![]() ,
,
![]() .
.
Матричное
уравнение вида
![]() имеет решение, если матрицы
имеет решение, если матрицы
![]() и
и
![]() –
квадратные матрицы одинакового порядка
и матрица
–
квадратные матрицы одинакового порядка
и матрица
![]() –
невырожденная, т.е.
–
невырожденная, т.е.
![]() . В этом случае для матрицы
. В этом случае для матрицы
![]() существует обратная матрица
существует обратная матрица
![]() .
Умножая слева обе части уравнения
.
Умножая слева обе части уравнения
![]() на
на
![]() ,
получим
,
получим
![]() ,
где
,
где
![]() единичная матрица,
единичная матрица,
![]() искомая
матрица.
искомая
матрица.
Для
данной матрицы
![]() :
:
![]() . Следовательно, существует
. Следовательно, существует
![]() .
Найдем ее по формуле
.
Найдем ее по формуле
 , где
, где
![]() алгебраическое дополнение элемента
алгебраическое дополнение элемента
![]() матрицы
матрицы
![]() .
Для данной матрицы
.
Для данной матрицы
![]() :
:
![]() . Тогда
. Тогда
![]()
и
![]()
![]() .
.
Ответ
:
![]() .
.
2)
Найти неизвестную матрицу
![]() из уравнения
из уравнения
![]() .
.
Решение.
Исходное уравнение запишем в матричной форме
![]() ,
где
,
где
![]() ,
,
![]() .
.
Матричное
уравнение вида
![]() имеет решение, если матрицы
имеет решение, если матрицы
![]() и
и
![]() –
квадратные матрицы одинакового порядка
и
–
квадратные матрицы одинакового порядка
и
![]() , т.е. для матрицы
, т.е. для матрицы
![]() существует обратная матрица
существует обратная матрица
![]() .
Умножая справа обе части уравнения
.
Умножая справа обе части уравнения
![]() на
на
![]() ,
получим
,
получим
![]() , где
, где
![]() единичная матрица, или
единичная матрица, или
![]() ,
или
,
или
![]() искомая
матрица.
искомая
матрица.
Для
данной матрицы
![]() :
:
![]() . Следовательно, существует
. Следовательно, существует
![]() .
Найдем ее по формуле, указанной в примере
1), имеем
.
Найдем ее по формуле, указанной в примере
1), имеем
![]() и
и
![]() .
.
Тогда
![]()
![]() .
.
Ответ
:
![]() .
.
Индивидуальные задания
Вариант № 1
1.1.
 1.2.
1.2.
 1.3.
1.3.

1.4.

1.5.
![]() ,
,
![]() 1.6.
1.6.![]()
Вариант № 2
2.1.
 2.2.
2.2.
 2.3.
2.3.

2.4.

2.5.
![]() ,
,
![]() 2.6.
2.6.
![]()
Вариант № 3
3.1
 3.2.
3.2.
 3.3.
3.3.

3.4.

3.5.
![]() ,
,
![]() 3.6.
3.6.![]()
Вариант № 4
4. 1.
 4.2.
4.2.
 4.3.
4.3.

4.4.

4.5.
![]() ,
,
![]() 4. 6.
4. 6.
![]()
Вариант № 5
5.1. 5.2.
5.2.
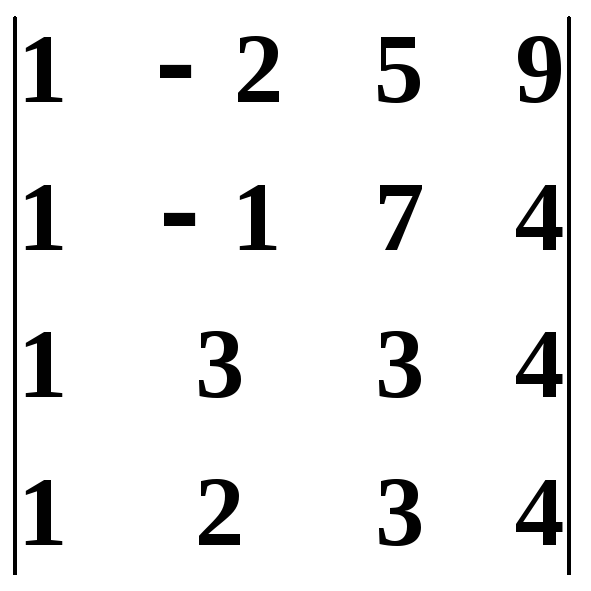 5.3.
5.3.

5.4.
5.5.
![]() ,
,
![]() 5.6.
5.6.![]()
Вариант № 6
6.1. 6.2.
6.2.
 6.3.
6.3.

6.4.

6.5.
![]() ,
,
![]() 6.6.
6.6.
![]()
Вариант № 7
7.1.
 7.2.
7.2.
 7.3.
7.3.
7.4.

7.5.
![]() ,
,
![]() 7. 6.
7. 6.
![]()
Вариант № 8
8.1.
 8.2.
8.2.
 8.3.
8.3.

8.4.

8.5.
![]() ,
,
![]() 8.6.
8.6.
![]()
Вариант № 9
9.1. 9.2.
9.2.
 9.3.
9.3.

9.4.

9.5.
![]() ,
,
![]() 9.6.
9.6.
![]()
Вариант № 10
10.1. 10.2.
10.2.
 10.3.
10.3.
10.4.

10.5.
![]() ,
,
![]() 10.6.
10.6.
![]()
Вариант № 11
11.1. 11.2.
11.2.
 11.3.
11.3.

11.4.

11.5.
![]() ,
,
![]() 11. 6.
11. 6.
![]()
Вариант № 12
12.1.
 12.2.
12.2.
 12.3.
12.3.

12.4.

12.5.
![]() ,
,
![]() 12.6.
12.6.
![]()
Вариант № 13
13.1.
 13.2.
13.2.
 13.3.
13.3.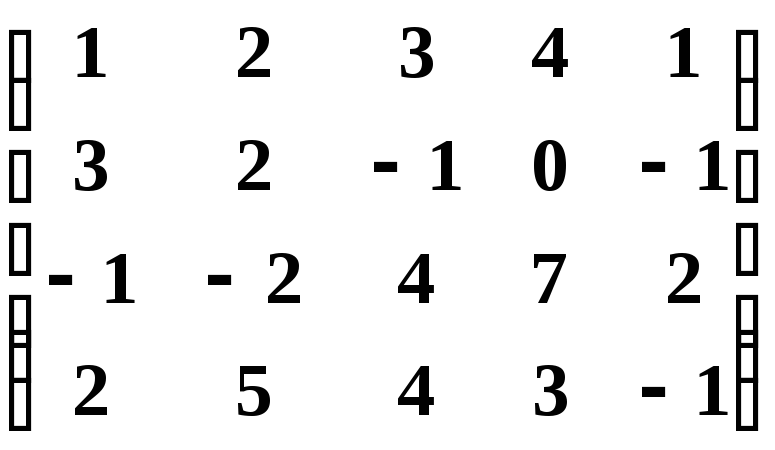
13.4.
13.5.
![]() ,
,
![]() 13.6.
13.6.
![]()
Вариант № 14
14.1.
 14.2.
14.2.
 14.3.
14.3.

14.4.
14.5.
![]() ,
,
![]() 14.6.
14.6.
![]()
Вариант № 15
15.1.
 15.2.
15.2.
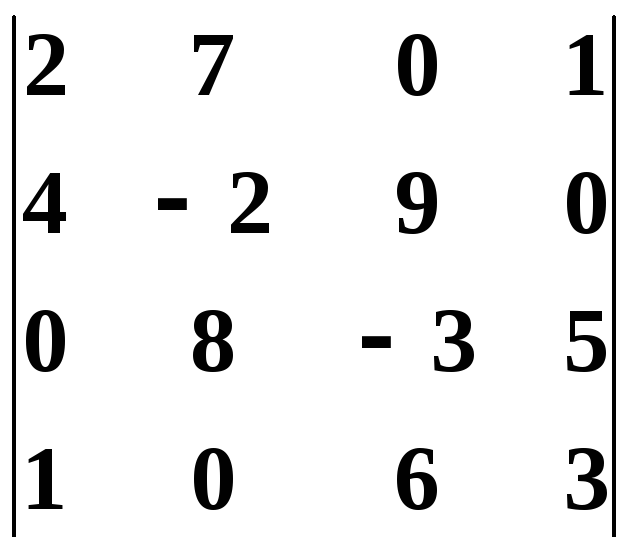 15.3.
15.3.

15.4.

15.5.
![]() ,
,
![]() 15.6.
15.6.
![]()
Вариант № 16
16.1.
 16.2.
16.2.
 16.3.
16.3.

16.4.

16.5.
![]() ,
,
![]() 16.6.
16.6.
![]()
Вариант № 17
17.1.
 17.2.
17.2.
 17.3.
17.3.

17.4.
17.5.
![]() ,
,
![]() 17.6.
17.6.
![]()
Вариант № 18
18.1.
 18.2.
18.2.
 18.3.
18.3.

18.4.
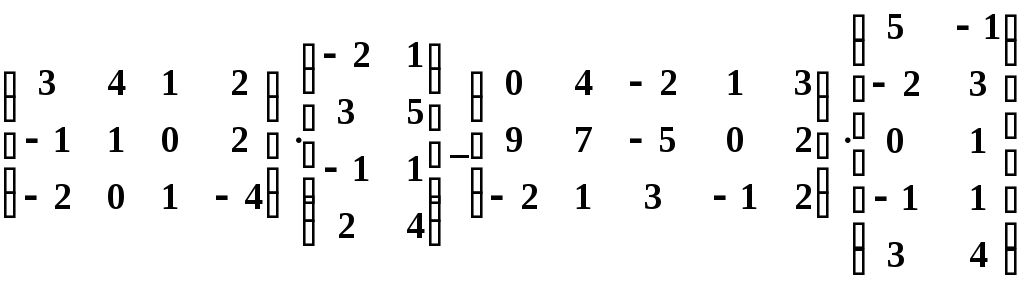
18.5.
![]() ,
,
![]() 18.6.
18.6.
![]()
Вариант № 19
19.1. 19.2.
19.2.
 19.3.
19.3.

19.4.

19.5.
![]() ,
,
![]() 19.6.
19.6.
![]()
Вариант № 20
20.1.
 20.2.
20.2.
 20.3.
20.3.

20.4.

20.5.
![]() ,
,
![]() 20.6.
20.6.
![]()
Вариант № 21
21.1.
 21.2.
21.2.

![]() 21.3.
21.3.

