29 Необходимые уравнения движения сплошных сред

Выделим мысленно объем V сплошной среды. Для него,,– главные векторы массовых сил, сил инерции и поверхностных сил. Необходимые уравнения движения выделенного объема

, (8.7.1)

. (8.7.2)

В уравнении (8.7.2) первое слагаемое – главный момент массовых сил и сил инерции, второе слагаемое – главный момент поверхностных сил.

Известно, что

. (8.7.3)

Тогда, (8.7.4) и из (8.7.1) получаем:

, (8.7.5)

откуда. (8.7.6)

Учитывая (8.7.3) и то, что ,,, уравнение (8.7.2) можно преобразовать к виду (см. подробнее в [1, с. 40]):

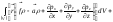
, (8.7.7)

откуда

. (8.7.8)

Здесь первое слагаемое равно нулю (см. (8.7.6)). Из равенства нулю остальных слагаемых (8.7.8) следует:

(8.7.9)

и,,. (8.7.10)

Таким образом, второе необходимое уравнение движения сплошной среды указывает, что тензор напряжения симметричен.

Уравнения движения сплошной среды в напряжениях в векторной и скалярной формах имеют вид:

; (8.7.11)

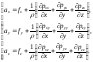(8.7.12)

При исследовании движения сплошной среды под действием заданных сил компоненты известны, а величиныподлежат определению. В системе (8.7.12) 3 уравнения с 10 неизвестными, т. е. это необходимые, но не достаточные уравнения. Недостающие уравнения в принципе не могут быть найдены методами классической механики– необходимо знание характеристик среды.

30 Уравнения движения идеальной жидкости

Идеальной называют жидкость, которая не оказывает сопротивления при скольжении одного ее слоя по другому. Сдвигающие напряжения при этом . Взаимодействие отдельных частей жидкости осуществляется лишь в виде сил нормального давления. Для напряжений внутренних сил, действующих на различно ориентированные площадки вблизи рассматриваемой точки жидкости, запишем:

, (9.1.1)

где – направляющие косинусы для внешней нормали к поверхности, ограничивающей выделенный объем среды. Спроецировав на оси декартовой системы координат, получим:

. (9.1.2)

Таким образом, давление в идеальной жидкости не зависит от ориентации площадки, к которой оно приложено – закон Паскаля.

Нормальное давление направлено внутрь объема, поэтому

, ,,, (9.1.3)

где – единичный вектор внешней нормали ;-вектор гидродинамического давления.

Основная задача гидродинамики – определение поля скоростей жидкости по заданным массовым силам, действующим в ней. Под полем скоростей здесь понимается совокупность векторов скоростей отдельных точек жидкости, заполняющей пространство. Таким образом, задача гидродинамики в данной постановке решается в переменных Эйлера.

Уравнение движения идеальной жидкости запишем в виде:

. (9.1.4)

Отсюда несложно перейти к уравнению Эйлера:

. (9.1.5)

К этому уравнению следует добавить уравнение непрерывности:

. (9.1.6)

В случае сжимаемой жидкости при заданных f уравнения (9.1.5) и (9.1.6) (в скалярной записи это 4 уравнения) содержат 5 неизвестных функций координат и времени: плотность, давление и 3 компонента скорости. Для решения системы нужно дополнительное условие.

Для идеальной несжимаемой жидкости , и система уравнений имеет вид:

(9.1.7)

Физическое состояние жидкости определяют давление, плотность, температура. Эти параметры не являются независимыми. Например, плотность может быть функцией только давления:

. (9.1.8)

Жидкость в этом случае называют баротропной.

Исходная система уравнений содержит нелинейные дифференциальные уравнения первого порядка. Их решение совместно с (9.1.8) содержит произвольные функции и постоянные, определяемые из начальных и граничных условий. Начальные условия: при t = 0

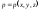,,; (9.1.9)

граничные условия вдоль неподвижной поверхности с нормалью :

или , (9.1.10)

где – уравнение поверхности. (9.1.10) – пример кинематического граничного условия, накладывающего ограничение на скорость жидкости. Если жидкость соприкасается с другой неподвижной средой, то вдоль границ сред давление постоянно:

р = р₀, (9.1.11)

что накладывает ограничение на поверхностные силы и является примером динамического граничного условия.

Введем в уравнение Эйлера в явном виде вектор завихренности :

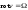. (9.1.12)

Это уравнение Ламба-Громеки. В ряде случаев оно удобнее уравнения Эйлера. Для баротропной жидкости () это уравнение может быть записано в виде:

. (9.1.13)

Преобразуя уравнение Эйлера для баротропной жидкости (см. подробнее в [1, с. 39–40]), можно получить уравнение Гельмгольца:

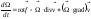, (9.1.14)

которое в случае несжимаемой жидкости () м потенциальности массовых сил () имеет простой вид

. (9.1.15)