18 Затухающие колебания

До сих пор мы подразумевали, что движение тел происходит в пустоте или, по крайней мере, можно пренебречь влиянием среды на это движение. В действительности при движении тела в среде последняя оказывает сопротивление, стремящееся замедлить движение; механическая энергия движущегося тела при этом переходит в тепловую энергию (диссипируется). В этих условиях процесс движения уже не чисто механический, а его рассмотрение требует учета движения среды и внутреннего теплового состояния как среды, так и тела. В общем случае задача о движении тела в среде выходит за рамки механики.

Однако в ряде случаев движение тела в среде может быть описано с помощью механических уравнений движения путем введения в них некоторых дополнительных членов. Сюда относятся колебания с частотами, малыми по сравнению с характерными для внутренних диссипативных процессов в среде частотами. При выполнении этого условия можно считать, что на тело действует сила трения, зависящая только от его скорости для заданной однородной среды. При малых скоростях эта сила трения пропорциональна скорости. Тогда дифференциальное уравнение движения в случае малых колебаний имеет вид:

(5.3.1)

где –коэффициент сопротивления (определяется свойствами среды и формой тела; например, в формуле Стокса , где– вязкость,– радиус движущегося в вязкой среде шара). Прирешением (5.3.1) будет, где,– начальная фаза (см. (5.1.10)).

Обозначим (5.3.2)

тогда(5.3.3)

–коэффициент затухания. Это однородное дифференциальное уравнение второго порядка, общее решение которого можно представить в виде

(5.3.4)

где – корни характеристического уравнения

(5.3.5)

При этом возможны следующие случаи: 1) ; 2); 3). Рассмотрим каждый из них.

1) 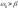– силы трения меньше квазиупругих сил.

(5.3.6)

(5.3.7)

Здесь(5.3.8)

комплексно-сопряженные числа. Тогда

(5.3.9)(использована формула Эйлера 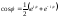). Полученное уравнение описывает колебательное движение тела (частицы), амплитуда которого (5.3.10)

убывает с течением времени по экспоненциальному закону (рисунок 5.3.1).

Рисунок 5.3.1

Скорость убывания амплитуды характеризуется коэффициентом затухания ;за время релаксации амплитуда уменьшается враз. Это не периодический процесс, т. к. нельзя указать период, для которого. Но периодичность есть в том смысле, что через равные промежутки временисистема проходит через положение равновесия, двигаясь в одну и ту же сторону.–условный период затухающих колебаний:

(5.3.11)

При малых значениях и

(5.3.12)

Таким образом , что вполне очевидно, действие сил трения замедляет движение.

Затухающие колебания характеризуются декрементом затухания – отношением двух значений амплитуды, измеренных в моменты времени, разделенные условным периодом :(5.3.13)

Но чаще используют логарифмический декремент затухания

(5.3.14)

Несложно убедиться, что логарифмический декремент затухания – величина, обратная числу колебаний за время релаксации:

(5.3.15)

Полная энергия системы

(5.3.16) где 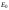– начальное значение энергии. Приимеем

(5.3.17)т. е. запас энергии убывает быстрее амплитуды.

2) – силы трения больше квазиупругих сил. Оба корня характеристического уравнения вещественны и отрицательны. Движение системы состоит в асимптотическом приближении к положению равновесия по закону

(5.3.18)

Такое движение называют апериодическим затуханием. Два возможных варианта такого движения представлены на рисунке 5.3.2.

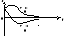
Рисунок 5.3.2 Рисунок 5.3.3

3) – особый случай апериодического затухания (см. рисунок 5.3.3):

(5.3.19)

Для системы с несколькими степенями свободы обобщенные силы трения, соответствующие координатам , являются линейными функциями скоростей вида(5.3.20)

Механические соображения не позволяют сделать вывод о симметричности коэффициентов по индексам, но в статистической физике доказывается, что(5.3.21)

Тогда выражения (5.3.20) могут быть записаны в виде производных

от квадратичной формы, называемой диссипативной функцией (5.3.23)

Силы (5.3.23) должны быть добавлены к правой части уравнений Лагранжа:

(5.3.24)

Диссипативная функция определяет интенсивность диссипации энергии в системе (можно показать, что скорость изменения энергии ). Поскольку при уменьшении энергии, то квадратичная форма (5.3.23) существенно положительна.

Уравнения колебаний при наличии трения имеют вид:

(5.3.25)

Положив в этих уравнениях(5.3.26)

получим систему линейных алгебраических уравнений для определения постоянных :

(5.3.27)

Характеристическое уравнение этой системы – уравнение степени относительно:

(5.3.28)

Поскольку все коэффициенты этого уравнения вещественны, то его корни либо вещественны, либо попарно комплексно сопряжены. При этом вещественные корни непременно отрицательны, а комплексные имеют отрицательную вещественную часть (в противном случае координаты и скорости, а значит, и энергия возрастали бы экспоненциально, в то время как наличие диссипативных сил должно приводить к уменьшению энергии).